Ex-5.1, (Part - 1) Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1 . x3+x−3x2−3
SOLUTION :
Taking x common in x3+x
=x(x2+1)−3x2−3
Taking – 3 common in −3x2−3
=x(x2+1)−3(x2+1)
Now , we take (x2+1) common
=(x2+1) (x – 3)
∴ x3+x−3y2−3 =(x2+1) (x – 3)
Q2 . a(a+b)3−3a2b(a+b)
SOLUTION :
Taking (a + b) common in the two terms
= (a + b) {a(a + b) ² – 3a ²b}
Now, using (a+b)2=a2+b2+2ab
=(a+b){a(a2+b2+2ab)−3a2b}
=(a+b){a3+ab2+2a2b−3a2b}
=(a+b){a3+ab2−a2b}
=(a+b)p{a2+b2−ab}
=p(a+b)(a2+b2−ab)
∴a(a+b)3−3a2b(a+b)=a(a+b)(a2+b2−ab)
Q3 . x(x3−y3)+3xy(x−y)
SOLUTION :
Elaborating x3−y3 using the identity x3−y3=(x−y)(x2+xy+y2)
=x(x−y)(x2+xy+y2)+3xy(x−y)
Taking common x( x-y ) in both the terms
=x(x−y)(x2+xy+y2+3y)
∴ x(x3−y3)+3xy(x−y)= x(x−y)(x2+xy+y2+3y)
Q4 . a2x2+(ax2+1)x+a
SOLUTION :
We multiply x(ax2+1)=ax3+x
=a2x2+ax3+x+a
Taking common ax2 in (a2x2+ax3) and 1in ( x + a )
=ax2(a+x)+1(x+a)
=ax2(a+x)+1(a+x)
Taking ( a + x ) common in both the terms
=(a+x)(ax2+1)
∴ a2x2+(ax2+1)x+a =(a+x)(ax2+1)
Q5 . x2+y−xy−x
SOLUTION :
On rearranging
x2−xy−x+y
Taking x common in the (x2−xy) and -1 in(-x+y )
=x( x – y ) – 1 ( x – y )
Taking ( x – y ) common in the terms
=( x – y )( x – 1 )
latex]∴\)x2+y−xy−x =( x – y )( x – 1 )
Q6 . x3−2x2b+3xy2−6y3
SOLUTION :
Taking x2 common in (x3−2x2y) and +3y2 common in (3xy2−6y3)
= x2(x−2y)+3y2(x−2y)
Taking ( x – 2y ) common in the terms
= (x−2y)(x2+3y2)
latex]∴\) x3−2x2y+3xy2−6y3 = (x−2y)(x2+3y2)
Q7 . 6ab−b2+12ac−2bc
SOLUTION :
Taking b common in (6ab−b2) and 2c in ( 12ac – 2bc )
=b( 6a – b ) + 2c ( 6a – b )
Taking ( 6a – b ) common in the terms
=( 6a – b )( b + 2c )
latex]∴\)6ab−b2+12ac−2bc =( 6a – b )( b + 2c )
Q8 .
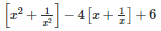
SOLUTION :
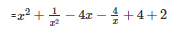
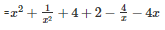
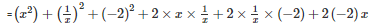
Using identity
x2+y2+z2+2xy+2yz+2zx=(x+y+z)2
We get,
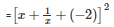
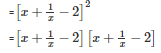
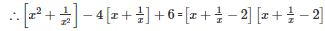
Q9 . x( x- 2 )( x – 4 ) + 4x – 8
SOLUTION :
=x( x – 2 )( x – 4 ) + 4( x – 2 )
Taking ( x – 2 ) common in both the terms
=( x – 2 ){x( x – 4 ) + 4}
=( x – 2 ) {x2−4x+4}
Now splitting the middle term of x2−4x+4
=( x – 2 ){ x2−2x−2x+4}
=( x – 2 ){ x( x – 2 ) -2( x -2 )}
=( x – 2 ){( x – 2 )( x- 2 )}
=( x – 2 )( x – 2 )( x – 2 )
=(x−2)3
∴ x( x- 2 )( x – 4 ) + 4x – 8=(x−2)3
Q10 .( x + 2 ) (x2+25)−10x2−20x
SOLUTION :
( x + 2 ) (x2+25)-10x ( x + 2 )
Taking ( x + 2 ) common in both the terms
=( x + 2 ) (x2+25−10x)
=( x + 2 ) (x2−10x+25)
Splitting the middle term of (x2−10x+25)
=( x + 2 ) (x2−5x−5x+25)
=( x + 2 ){ x (x – 5 ) -5 ( x – 5 )}
=( x + 2 )( x – 5 )( x – 5 )
∴ ( x + 2 ) (x2+25)−10x2 – 20x=( x + 2 )( x – 5 )( x – 5 )
Q11 . 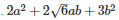
SOLUTION :
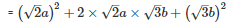
Using the identity (p+q)2=p2+q2+2pq
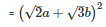
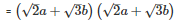
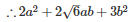
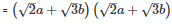
Q 12 . (a−b+c)2+(b−c+a)2+2(a−b+c)×(b−c+a)
SOLUTION :
Let ( a – b + c ) = x and ( b – c + a ) = y
- =x2+y2+2xy
Using the identity (a+b)2=a2+b2+2ab
=(x+y)2
Now , substituting x and y
- (a–b+c+b−c+a)2
Cancelling –b , +b & +c , -c
=(2a)2
=4a2
∴(a−b+c)2+(b−c+a)2+2(a−b+c)×(b−c+a)=4a2
Q13 . a2+b2+2(ab+bc+ca)
SOLUTION :
=a2+b2+2ab+2bc+2ca
Using the identity (p+q)2=p2+q2+2pq
We get,
= (a+b)2 + 2bc + 2ca
= (a+b)2 + 2c( b + a )
Or (a+b)2 + 2c( a + b )
Taking ( a + b ) common
= ( a + b )( a + b + 2c )
∴ a2+b2+2(ab+bc+ca) = ( a + b )( a + b + 2c )
Q14 . 4(x−y)2−12(x−y)(x+y)+9(x+y)2
SOLUTION :
Let ( x – y ) = x,( x + y ) = y
= 4x2−12xy+9y2
Splitting the middle term – 12 = -6 -6 also 4×9=−6×−6
=4x2−6xy−6xy+9y2
=2x( 2x – 3y ) -3y( 2x – 3y )
=( 2x – 3y ) ( 2x – 3y )
=(2x−3y)2
Substituting x = x – y & y = x + y
=[2(x−y)−3(x+y)]2=[ 2x – 2y – 3x – 3y ]2
=(2x-3x-2y-3y )²
=[−x−5y]2
=[(−1)(x+5y)]2
=(x+5y)2 [∵ (-1)2 = 1]
∴ 4(x−y)2−12(x−y)(x+y)+9(x+y)2=(x+5y)2
Q 15 . a2−b2+2bc−c2
SOLUTION :
a2−(b2−2bc+c2)
Using the identity (a−b)2=a2+b2−2ab
= a2−(b−c)2
Using the identity a2−b2=(a+b)(a−b)
=( a + b – c )( a – ( b – c ))
=( a + b – c )( a – b + c )
∴ a2−b2+2bc−c2=( a + b – c )( a – b + c )
Q16 . a2+2ab+b2−c2
SOLUTION :
Using the identity (p+q)2=p2+q2+2pq
=(a+b)2−c2
Using the identity p2−q2=(p+q)(p−q)
=( a + b + c )( a + b – c )
∴ a2+2ab+b2−c2 =( a + b + c )( a + b – c )
Q 17 . a2+4b2−4ab−4c2
SOLUTION :
On rearranging
= a2−4ab+4b2−4c2
= (a)2−2×a×2b+(2b)2−4c2
Using the identity (a−b)2=a2+b2−2ab
=(a−2b)2−4c2
=(a−2b)2−(2c)2
Using the identity a2−b2=(a+b)(a−b)
=( a – 2b – 2c) ( a – 2b + 2c)
∴ a2+4b2−4ab−4c2 =( a – 2b – 2c) ( a – 2b + 2c)
Q18 . xy9−yx9
SOLUTION :
=xy(y8−x8)
=xy((y4)2−(x4)2)
Using the identity p2−q2= ( p + q )( p – q )
=xy(y4+x4)(y4−x4)
=xy(y4+x4)((y2)2−(x2)2)
Using the identity p2−q2= ( p + q )( p – q )
=xy(y4+x4)(y2+x2)(y2−x2)
= xy(y4+x4)(y2+x2)(y+x)(y−x)
= xy(x4+y4)(x2+y2)(x+y)(−1)(x−y)
∵(y−x)=−1(x−y)
=−xy(x4+y4)(x2+y2)(x+y)(x−y)
∴ xy9−yx9 = −xy(x4+y4)(x2+y2)(x+y)(x−y)
Q 19 . x4+x2y2+y4
SOLUTION :
Adding x2y2 and subtracting x2y2 to the given equation
= x4+x2y2+y4+x2y2−x2y2
= x4+2x2y2+y4−x2y2
= (x2)2+2×x2×y2+(y2)2−(xy)2
Using the identity (p+q)2=p2+q2+2pq
= (x2+y2)2−(xy)2
Using the identity p2−q2= ( p + q )( p – q )
= (x2+y2+xy)(x2+y2−xy)
∴ x4+x2y2+y4 = (x2+y2+xy)(x2+y2−xy)
FAQs on Ex-5.1, (Part - 1) Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of factorization of algebraic expressions in mathematics? |  |
| 2. How can factorization of algebraic expressions be used to solve equations? |  |
| 3. Can factorization of algebraic expressions be used to simplify fractions? |  |
| 4. Are there any specific methods or rules for factorization of algebraic expressions? |  |
| 5. How can factorization of algebraic expressions be applied in real-life situations? |  |
















