Ex-5.2, Operations On Rational Numbers, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Q1. Subtract the first rational number from the second in each of the following:
Solution.
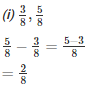
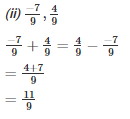
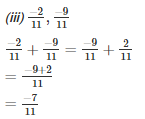
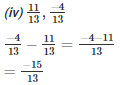
Q2. Evaluate each of the following:
Solution.
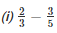
LCM of 3 and 5 is 15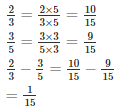
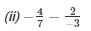
LCM of 3 and 7 is 21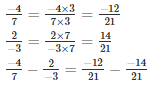
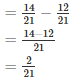
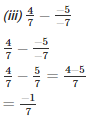
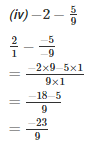
Q3. The sum of the two numbers is 5/9. If one of the numbers is 1/3, find the other.
Solution.
Required number = 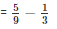
LCM of 3 and 9 is 9
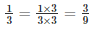
Therefore required number 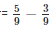
= 2/9
Q4. The sum of two numbers is −1/3. If one of the numbers is −12/3, find the other.
Solution.
Let the required number be x
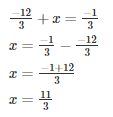
The required number is 11/3
Q5. The sum of two numbers is −4/3. If one of the numbers is -5, find the other.
Solution.
Let the required number be x
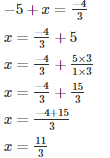
The required number is 11/3
Q6. The sum of two rational numbers is -8. If one of the numbers is −15/7, find the other.
Solution.
Let the required number be x
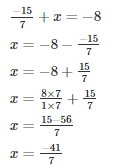
The required number is -41/7
Q7. What should be added to −7/8 so as to get 5/9?
Solution.
Let the required number be x
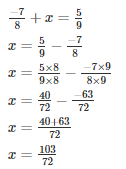
The required number is 103/72
Q8. What number should be added to -5/11 so as to get 26/33?
Solution.
Let the required number be x
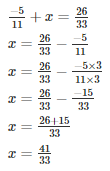
The required number is 41/33
Q9. What number should be added to −5/7 to get −2/3?
Solution.
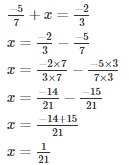
The required number is 1/21
Q10. What number should be subtracted from −5/3 to get 5/6?
Solution.
Let the required number be x
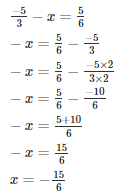
The required number is 15/6
Q11. What number should be subtracted from 3/7 to get 5/4?
Solution.
Let the required number be x
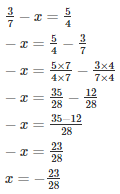
The required number is 23/28
Q12. What should be added to 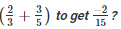
Solution.
Let the required number be x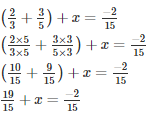
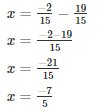
The required number is −7/5
Q13. What should be added to 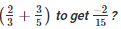
Solution.
Let the required number be x
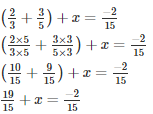
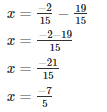
The required number is 59/30
Q14. What should be subtracted from 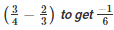
Solution.
Let the required number be x
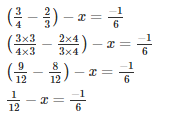
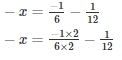
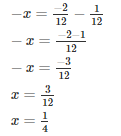
The required number is 1/4
Q15. Simplify:
Solution.

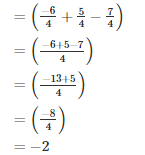
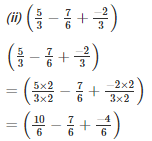
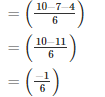
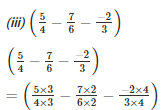

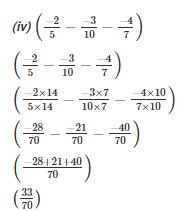
Q16. Fill in the blanks:
Solution.
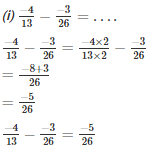
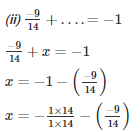
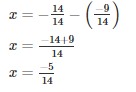
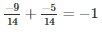
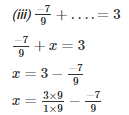
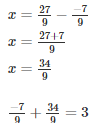
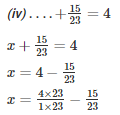
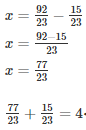
FAQs on Ex-5.2, Operations On Rational Numbers, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are rational numbers? |  |
| 2. How do we perform addition and subtraction of rational numbers? |  |
| 3. Can we multiply and divide rational numbers? |  |
| 4. What is the concept of the absolute value of a rational number? |  |
| 5. How do we compare rational numbers? |  |

|
Explore Courses for Class 7 exam
|

|

















