Ex-5.4, Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1 . a3+8b3+64c3−24abc
SOLUTION :
= (a)3+(2b)3+(4c)3−3×a×2b×4c
= (a+2b+4c)(a2+(2b)2+(4c)2−a×2b−2b×4c−4c×a) [∵a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)]
= (a+2b+4c)(a2+4b2+16c2−2ab−8bc−4ac)
∴ a3+8b3+64c3−24abc = (a+2b+4c)(a2+4b2+16c2−2ab−8bc−4ac)
Q 2 . x3−8y3+27z3+18xyz
SOLUTION :
= x3−(2y)3+(3z)3−3×x×(−2y)(3z)
= (x+(−2y)+3z)(x2+(−2y)2+(3z)2−x(−2y)−(−2y)(3z)−3z(x)) [∵a3+b3+c3−3abc=(a+b+c)(a2+b2+c2−ab−bc−ca)]
=(x+(−2y)+3z)(x2+4y2+9z2+2xy+6yz−3zx)
∴ x3−8y3+27z3+18xyz =(x+(−2y)+3z)(x2+4y2+9z2+2xy+6yz−3zx)
Q 3 . 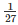 x3−y3+125z3+5xyz
x3−y3+125z3+5xyz
SOLUTION :
= 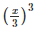 +(−y)3+(5z)3−3×
+(−y)3+(5z)3−3×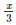 (−y)(5z)
(−y)(5z)
= (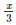 +(−y)+5z)((
+(−y)+5z)((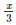 )2+(−y)2+(5z)2−
)2+(−y)2+(5z)2−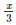 (−y)−(−y)5z−5z(
(−y)−(−y)5z−5z(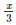 ))
))
= (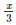 −y+5z)
−y+5z)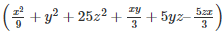
∴ 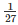 x3−y3+125z3+5xyz = (
x3−y3+125z3+5xyz = (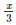 −y+5z)
−y+5z)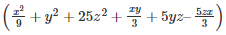
Q 4 . 8x3+27y3−216z3+108xyz
SOLUTION :
= (2x)3+(3y)3+(−6y)3−3(2x)(3y)(−6z)
= (2x+3y+(−6z))((2x)2+(3y)2+(−6z)2−2x×3y−3y(−6z)−(−6z)2x)
= (2x+3y+(−6z))(4x2+9y2+36z2−6xy+18yz+12zx)
∴ 8x3+27y3−216z3+108xyz = (2x+3y+(−6z))(4x2+9y2+36z2−6xy+18yz+12zx)
Q 5 . 125+8x3−27y3+90xy
SOLUTION :
= (5)3+(2x)3+(−3y)3−3×5×2x×(−3y)
= (5+2x+(−3y))(52+(2x)2+(−3y)2−5(2x)−2x(−3y)−(−3y)5)
= (5+2x−3y)(25+4x2+9y2−10x+6xy+15y)
∴ 125+8x3−27y3+90xy = (5+2x−3y)(25+4x2+9y2−10x+6xy+15y)
Q 6 . (3x−2y)3+(2y−4z)3+(4z−3x)3
SOLUTION :
Let (3x−2y) = a , (2y−4z) = b , (4z−3x) = c
∴ a+b+c=3x−2y+2y−4z+4z−3x=0
∵ a+b+c=0 ∴ a3+b3+c3=3abc
= 3(3x−2y)(2y−4z)(4z−3x)
∴ (3x−2y)3+(2y−4z)3+(4z−3x)3 = 3(3x−2y)(2y−4z)(4z−3x)
Q 7 . (2x−3y)3+(4z−2x)3+(3y−4z)3
SOLUTION :
Let 2x – 3y = a , 4z – 2x = b , 3y – 4z = c
∴ a+b+c=2x−3y+4z−2x+3y−4z=0
∵ a+b+c=0 ∴ a3+b3+c3=3abc
= 3(2x−3y)(4z−2x)(3y−4z)
∴ (2x−3y)3+(4z−2x)3+(3y−4z)3 = 3(2x−3y)(4z−2x)(3y−4z)
Q 8 . 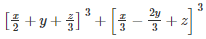
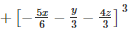
SOLUTION :
Let 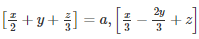
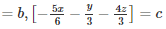
a+b+c= 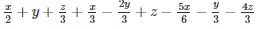
a+b+c= 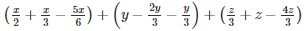
a+b+c= 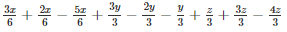
a+b+c= 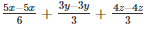
a+b+c= 0
∵a+b+c=0 ∴ a3+b3+c3=3abc
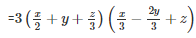
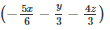
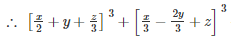
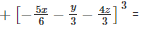
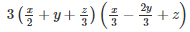
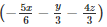
Q 9 . (a−3b)3+(3b−c)3+(c−a)3
SOLUTION :
Let a – 3b = x , 3b – c = y , c – a = z
x+y+z=a−3b+3b−c+c−a=0
(∵ x+y+z=0) ∴ x3+y3+z3=3xyz
= 3(a−3b)(3b−c)(c−a)
∴ (a−3b)3+(3b−c)3+(c−a)3 = 3(a−3b)(3b−c)(c−a)
Q 10 . 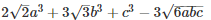
SOLUTION :
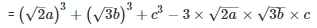
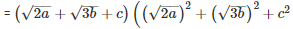
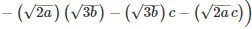
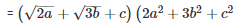
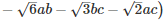
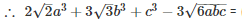
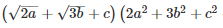
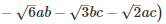
Q 11 .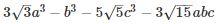
SOLUTION :
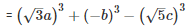
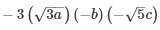
= 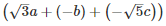
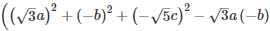
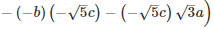
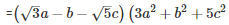
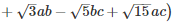
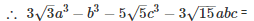
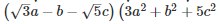
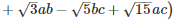
Q 12 . 8x3−125y3+216+180xy
SOLUTION :
= (2x)3+(−5y)3+63−3×(2x)(−5y)(6)
= (2x+(−5y)+6)((2x)2+(−5y)2+62−2x×(−5y)−(−5y)6−6(2x))
= (2x−5y+6)(4x2+25y2+36+10xy+30y−12x)
∴ 8x3−125y3+216+180xy = (2x−5y+6)(4x2+25y2+36+10xy+30y−12x)
Q 13 . 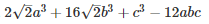
SOLUTION :
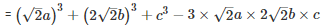
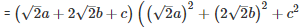
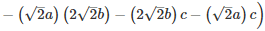
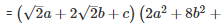
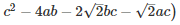
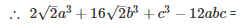
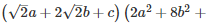
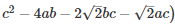
Q 14 . Find the value of x3+y3−12xy+64 when x + y = -4.
SOLUTION :
= x3+y3+64−12xy
= x3+y3+43−3(x)(y)(4)
= (x+y+4)(x2+y2+42−xy−y×4−4×x)
= (−4+4)(x2+y2+16−xy−4y−4x) [∵x+y=−4]
=0
∴ x3+y3−12xy+64 = 0
Q 15 . MULTIPLY :
(i) . x2+y2+z2−xy+xz+yzbyx+y−z
SOLUTION :
= (x2+y2+z2−xy+xz+yz)(x+y−z)
= x3+y3+z3−3xyz
(ii) . x2+4y2+z2+2xy+xz−2yzbyx−2y−z
SOLUTION :
x2+(−2y)2+(−z)2−(−2y)(−z)−(−z)(x) = x3+(−2y)3+(−z)3−3x(−2y)(−z)
⇒x2+4y2+z2+2xy−2yz+zx=x3−8y3−z3−6xyz
(iii) . x2+4y2+2xy−3x+6y+9 by (x−2y+3)
SOLUTION :
(x)2+(−2y)2+(3)2−(x)(−2y)−(−2y)(3)−3(x)= (x)3+(−2y)3+33−3(x)(−2y)(3)
⇒x2+4y2+9+2xy+6y−3x= x3−8y3+27+18xy
(iv) . 9x2+25y2+15xy+12x−20y+16by3x−5y+4
SOLUTION :
(3x)2+(5y)2+42−(−3x)(5y)−(5y)(4)−(4)(−3x)=(−3x)3+(5y)3+43−3(−3x)(5y)(4)
⇒9x2+25y2+16+15xy−20y+12x=−27x3+125y3+64+180xy
FAQs on Ex-5.4, Factorization Of Algebraic Expressions, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. How do I factorize algebraic expressions in class 9? |  |
| 2. What is the importance of factorization in algebraic expressions? |  |
| 3. Can you give an example of factorizing an algebraic expression? |  |
| 4. Are there any specific methods or techniques for factorizing algebraic expressions? |  |
| 5. Can factorization be used to solve equations? |  |
















