Ex-6.1, Exponents, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Q1. Find the values of each of the following :
(i) 132
(ii) 73
(iii) 34
Sol:
(i) 132 = 13×13
= 169
(ii) 73 = 7×7×7
= 4
(iii) 34 = 3×3×3×3
= 81
Q2. Find the value of each of the following :
(i) (−7)2
(ii) (−3)4
(iii) (−5)5
Sol:
We know that if ‘a’ is a natural number, then
(−a) even number = positive number
(−a) odd number = negative number
We have,
(i) (−7)2 = (-7) ×(-7)
= 49
(ii) (−3)4 = (-3) ×(-3) ×(-3) ×(-3)
= 81
(iii) (−5)5 = (-5) ×(-5) ×(-5) ×(-5) ×(-5)
= -3125
Q3. Simply :
(i) 3×102
(ii) 22×53
(iii) 33×52
Sol:
(i) 3×102 = 3×10×10
= 3×100
= 300
(ii) 22×53 = 2×2×5×5×5
= 4×125
= 500
(iii) 33×52 = 3×3×3×5×5
= 27×25
= 675
Q4. Simply :
(i) 32×104
(ii) 24×32
(iii) 52×34
Sol:
(i) 32×104 = 3×3×10×10×10×10
= 9×10000
= 90000
(ii) 24×32 = 2×2×2×2×3×3
= 16×9
= 144
(iii) 52×34 = 5×5×3×3×3×3
= 25×81
= 2025
Q5. Simply :
(i) (−2)×(−3)3
(ii) (−3)2×(−5)3
(iii) (−2)5×(−10)2
Sol:
(i) (−2)×(−3)3 = (-2) ×(-3) ×(-3) ×(-3)
= (-2) ×(-27)
= 54
(ii) (−3)2×(−5)3 = (-3) ×(-3) ×(-5) ×(-5) ×(-5)
= 9×(-125)
= -1125
(iii) (−2)5×(−10)2 = (-2) ×(-2) ×(-2) ×(-2) ×(-2) ×(-10) ×(-10)
= (-32) × 100
= -3200
Q6. Simply :
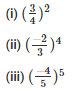
Sol:
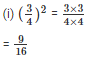
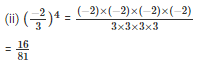
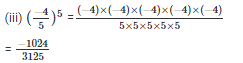
Q7. Identify the greater number in each of the following
(i) 25 or 52
(ii) 34 or 43
(iii) 35 or 53
Sol:
(i) 25 or 52
= 25 = 2×2×2×2×2
= 32
= 52 = 5×5
= 25
Therefore, 25 52
(ii) 34 or 43
= 34 = 3×3×3×3
= 81
= 43 = 4×4×4
= 64
Therefore, 34 43
(iii) 35 or 53
= 35 = 3×3×3×3×3
= 243
= 53 = 5×5×5
= 125
Therefore, 35 53
(iii) 35 or 53
= 35 = 3×3×3×3×3
= 243
= 53 = 5×5×5
= 125
Therefore, 35 53
Q8. Express each of the following in exponential form
(i) (-5) ×(-5) ×(-5)
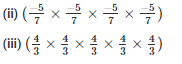
Sol:
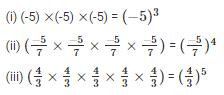
Q9. Express each of the following in exponential form
(i) x ×x ×x ×x ×a ×a ×b ×b ×b
(ii) (-2) ×(-2) ×(-2) ×(-2) ×a×a×a
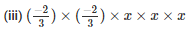
Sol:
(i) x ×x ×x ×x ×a ×a ×b ×b ×b = x4a2b3
(ii) (-2) ×(-2) ×(-2) ×(-2) ×a×a×a = (−2)4a3
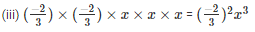
Q10. Express each of the following numbers in exponential form
(i) 512
(ii) 625
(iii) 729
Sol:
(i) 512 = 29
(iii) 625 = 54
(iii) 729 = 36
Q11. Express each of the following numbers as a product of powers of their prime factors
(i) 36
(ii) 675
(iii) 392
Sol:
(i) 36 = 2×2×3×3
= 22×32
(ii) 675 = 3×3×3×5×5
= 33×52
(iii) 392 = 2×2×2×7×7
= 23×72
Q12. Express each of the following numbers as a product of powers of their prime factors
(i) 450
(ii) 2800
(iii) 24000
Sol:
(i) 450 = 2×3×3×5×5
= 2×32×52
(ii) 2800 = 2×2×2×2×5×5×7
= 24×52×7
(iii) 24000 = 2×2×2×2×2×2×3×5×5×5
= 25×3×53
Q13. Express each of the following as a rational number of the form p/q
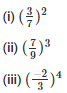
Sol:
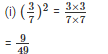
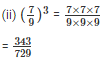
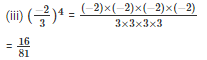
Q14. Express each of the following rational numbers in power notation
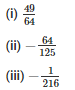
Sol:
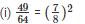
Because 72 = 49 and 82 = 64
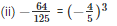
Because 43 = 64 and 53 = 125
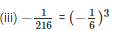
Because 13 = 1 and 63 = 216
Q15. Find the value of the following
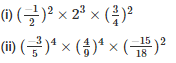
Sol:
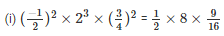
= 9/8
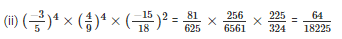
Q16. If a= 2 and b = 3, the find the values of each of the followimg
(i) (a+b)a
(ii) (ab)b
(iii) (b/a)b
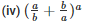
Sol:
(i) (a+b)a = (2+3)2
= (5)2
= 25
(ii) (ab)b = (2×3)3
= (6)3
= 216
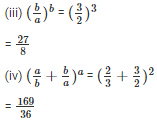
FAQs on Ex-6.1, Exponents, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are exponents? |  |
| 2. How do exponents work? |  |
| 3. What are the laws of exponents? |  |
| 4. How do exponents relate to multiplication and division? |  |
| 5. How are exponents used in real-life applications? |  |






















