All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Notes  >  RD Sharma Solutions for Class 9 Mathematics  >  RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths

RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download

Q1. x3+6x2+11x+6

Sol:

Given polynomial, f(x) = x3+6x2+11x+6

The constant term in f(x) is 6

The factors of 6 are ±1, ±2, ±3, ±6

Let, x + 1 = 0

⇒ x = -1

Substitute the value of x in f(x)

f(-1) = (−1)3+6(−1)2+11(−1)+6

= -1 + 6 -11 + 6

= 12 – 12

= 0

So, (x + 1) is the factor of f(x)

Similarly, (x + 2) and (x + 3) are also the factors of f(x)

Since, f(x) is a polynomial having a degree 3, it cannot have more than three linear factors.

∴ f(x) = k(x + 1)(x + 2)(x + 3)

⇒ x3+6x2+11x+6 = k(x + 1)(x + 2)(x + 3)

Substitute x = 0 on both the sides

⇒ 0 + 0 + 0 + 6 = k(0 +1)(0 + 2)(0 + 3)

⇒ 6 = k(1*2*3)

⇒ 6 = 6k

⇒ k = 1

Substitute k value in f(x) = k(x + 1)(x + 2)(x + 3)

⇒ f(x) = (1)(x + 1)(x + 2)(x + 3)

⇒ f(x) = (x + 1)(x + 2)(x + 3)

∴ x3+6x2+11x+6 = (x + 1)(x + 2)(x + 3)


Q2. x3+2x2–x–2

Sol:

Given, f(x) = x3+2x2–x–2

The constant term in f(x) is -2

The factors of (-2) are ±1, ±2

Let , x – 1 = 0

⇒ x = 1

Substitute the value of x in f(x)

f(1) = (1)3+2(1)2–1–2

= 1 + 2 – 1 – 2

= 0

Similarly , the other factors (x + 1) and (x + 2) of f(x)

Since, f(x) is a polynomial having a degree 3, it cannot have more than three linear factors.

∴ f(x) = k(x – 1)(x + 2)(x + 1)

x3+2x2–x–2 = k(x – 1)(x + 2)(x + 1)

Substitute x = 0 on both the sides

0 + 0 – 0 – 2 = k(-1)(1)(2)

⇒  – 2 = -2k

⇒  k = 1

Substitute k value in f(x)  = k(x – 1)(x + 2)(x + 1)

f(x) = (1)(x – 1)(x + 2)(x + 1)

⇒ f(x) =  (x – 1)(x + 2)(x + 1)

So, x3+2x2–x–2 = (x – 1)(x + 2)(x + 1)


Q3. x3–6x2+3x+10

Sol:

Let, f(x) = x3–6x2+3x+10

The constant term in f(x) is 10

The factors of 10 are ±1, ±2, ±5, ±10

Let , x + 1 = 0

⇒ x = -1

Substitute the value of x in f(x)

f(-1) = (−1)3–6(−1)2+3(−1)+10

= -1 – 6 – 3 + 10

= 0

Similarly , the other factors (x – 2) and (x – 5) of f(x)

Since, f(x) is a polynomial having a degree 3, it cannot have more than three linear factors.

∴ f(x) = k(x + 1)(x – 2)(x – 5 )

Substitute x = 0 on both sides

⇒ x3–6x2+3x+10 = k(x + 1)(x – 2)(x – 5)

⇒ 0 – 0 + 0 + 10 = k(1)(-2)(-5)

⇒ 10 = k(10)

⇒ k = 1

Substitute k = 1 in f(x) = k(x + 1)(x – 2)(x – 5)

f(x) = (1)(x + 1)(x – 2)(x – 5)

so, x3–6x2+3x+10 = (x + 1)(x – 2)(x – 5)


Q4. x4–7x3+9x2+7x–10

Sol:

Given, f(x) = x4–7x3+9x2+7x–10

The constant term in f(x) is 10

The factors of 10 are ±1, ±2, ±5, ±10

Let , x – 1 = 0

⇒ x = 1

Substitute the value of x in f(x)

f(x) = 14–7(1)3+9(1)2+7(1)–10

= 1 – 7 + 9 + 7 – 10

= 10 – 10

= 0

(x – 1)  is the factor of f(x)

Simarly, the other factors are (x + 1) ,(x – 2) , (x – 5)

Since, f(x) is a polynomial of degree 4. So, it cannot have more than four linear factor.

So, f(x) = k(x – 1)(x + 1)(x – 2)(x – 5)

⇒ x4–7x3+9x2+7x–10 = k(x – 1)(x + 1)(x – 2)(x – 5)

Put x = 0 on both sides

0 – 0 + 0 – 10  =  k(-1)(1)(-2)(-5)

– 10 = k(-10)

⇒ k = 1

Substitute k = 1 in  f(x) = k(x – 1)(x + 1)(x – 2)(x – 5)

f(x) = (1)(x – 1)(x + 1)(x – 2)(x – 5)

= (x – 1)(x + 1)(x – 2)(x – 5)

So, x4–7x3+9x2+7x–10 = (x – 1)(x + 1)(x – 2)(x – 5)


Q5. x4–2x3–7x2+8x+12

Sol:

Given , f(x) = x4–2x3–7x2+8x+12

The constant term f(x) is equal is 12

Tha factors of 12 are ±1, ±2, ±3, ±4, ±6, ±12

Let, x + 1 = 0

⇒ x = -1

Substitute the value of x in f(x)

f(-1) = (−1)4–2(−1)3–7(−1)2+8(−1)+12

= 1 + 2 – 7 – 8 + 12

= 0

So, x + 1 is factor of f(x)

Similarly, (x + 2), (x – 2), (x – 3) are also the factors of f(x)

Since, f(x) is a polynomial of degree 4 , it cannot have more than four linear factors.

⇒ f(x) = k(x + 1)(x + 2)(x – 3)(x – 2)

⇒ x4–2x3–7x2+8x+12 = k(x + 1)(x + 2)(x – 3)(x – 2)

Substitute x = 0 on both sides,

⇒ 0 – 0 – 0 + 12 = k(1)(2)(-2)(-3)

⇒ 12 = k12

⇒ k = 1

Substitute k = 1 in f(x) = k(x – 2)(x + 1)(x + 2)(x – 3)

f(x) = (x – 2)(x + 1)(x + 2)(x – 3)

so, x4–2x3–7x2+8x+12 = (x – 2)(x + 1)(x + 2)(x – 3)

Q6. x4+10x3+35x2+50x+24

Sol:

Given, f(x) = x4+10x3+35x2+50x+24

The constant term in f(x) is equal to 24

The factors of 24 are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24

Let, x + 1 = 0

⇒ x = -1

Substitute the value of x in f(x)

f(-1) = (−1)4+10(−1)3+35(−1)2+50(−1)+24

= 1 – 10 + 35 – 50 + 24

= 0

⇒ (x + 1) is the factor of f(x)

Similarly, (x + 2),(x + 3),(x + 4) are also the factors of f(x)

Since, f(x) is a polynomial of degree 4, it cannot have more than four linear factors.

⇒ f(x) = k(x + 1)(x + 2)(x + 3)(x + 4)

⇒ x4+10x3+35x2+50x+24 = k(x + 1)(x + 2)(x + 3)(x + 4)

Substitute x = 0 on both sides

⇒ 0 + 0 + 0 + 0 + 24 = k(1)(2)(3)(4)

⇒ 24 = k(24)

⇒ k = 1

Substitute k = 1 in f(x) = k(x + 1)(x + 2)(x + 3)(x + 4)

f(x) = (1)(x + 1)(x + 2)(x + 3)(x + 4)

f(x) = (x + 1)(x + 2)(x + 3)(x + 4)

hence, x4+10x3+35x2+50x+24 = (x + 1)(x + 2)(x + 3)(x + 4)


Q7.  2x4–7x3–13x2+63x–45

Sol :

Given, f(x) = 2x4–7x3–13x2+63x–45

The factors of constant term -45 are ±1, ±3, ±5, ±9, ±15, ±45

The factors of the coefficient of  x4 is 2. Hence possible rational roots of f(x) are

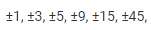
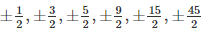
RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 MathematicsRD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics

Let, x – 1 = 0

⇒ x= 1

f(1) = 2(1)4–7(1)3–13(1)2+63(1)–45

= 2 – 7 – 13 + 63 – 45

= 0

Let, x – 3 = 0

⇒ x = 3

f(3) = 2(3)4–7(3)3–13(3)2+63(3)–45

= 162 – 189 – 117 + 189 – 45

= 0

So, (x – 1) and (x – 3) are the roots of f(x)

⇒ x2 – 4x + 3 is the factor of f(x)

Divide f(x) with x2 – 4x + 3 to get other three factors

By long division,

2x2 + x – 15

x2  – 4x + 3    2x4 – 7x3 – 13x2  + 63x – 45

2x4  – 8x3  + 6x2

(-)      (+)        (-)

x3   – 19x2  + 63x

x3     – 4x2     + 3x

(-)        (+)          (-)

– 15x2 + 60x – 45

(+)           (-)         (+)

0

⇒  2x4–7x3–13x2+63x–45 = (x2 – 4x + 3)(2x2 + x – 15)

⇒ 2x4–7x3–13x2+63x–45 = (x – 1) (x – 3)(2x2 + x – 15)

Now,

2x2 + x – 15 = 2x2+ 6x – 5x  – 15

= 2x(x + 3) – 5 (x + 3)

= (2x – 5) (x + 3)

So, 2x4–7x3–13x2+63x–45 = (x – 1)(x – 3)(x + 3)(2x – 5)


Q8. 3x3−x2–3x+1

Sol :

Given , f(x) = 3x3−x2–3x+1

The factors of constant term 1 is ±1

The factors of the coefficient of x2 = 3

The possible rational roots are ±1 ,1/3

Let, x – 1 = 0

⇒ x = 1

f(1) = 3(1)3−(1)2–3(1)+1

= 3 – 1 – 3 + 1

= 0

So, x – 1 is tha factor of f(x)

Now, divide f(x) with (x – 1) to get other factors

By long division method,

3x2 + 2x – 1

x – 1   3x3 – x2 – 3x + 1

3x3 – x2

(-)       (+)

2x2 – 3x

2x2 – 2x

(-)       (+)

-x + 1

-x + 1

(+)  (-)

0

⇒ 3x3−x2–3x+1 = (x – 1)( 3x2 + 2x – 1)

Now,

3x2 + 2x – 1 = 3x2 + 3x – x  – 1

= 3x(x + 1) -1(x + 1)

= (3x – 1)(x + 1)

Hence , 3x3−x2–3x+1 = (x – 1) (3x – 1)(x + 1)


Q9. x3−23x2+142x–120

Sol :

Let, f(x) = x3−23x2+142x–120

The constant term in f(x) is -120

The factors of -120 are ±1, ±2, ±3, ±4, ±5, ±6, ±8, ±10, ±12, ±15, ±20, ±24, ±30, ±40, ±60, ±120

Let, x – 1 = 0

⇒ x = 1

f(1) = (1)3−23(1)2+142(1)–120

= 1 – 23  + 142 – 120

= 0

So, (x – 1) is the factor of f(x)

Now, divide f(x) with (x – 1) to get other factors

By long division,

x2 – 22x + 120

x – 1   x3 – 23x2 + 142x – 120

x3 –   x2

(-)    (+)

-22x2 + 142x

-22x2  + 22x

(+)            (-)

120x – 120

120x – 120

(-)           (+)

0

⇒ x3 – 23x2 + 142x – 120 = (x  – 1) (x2 – 22x + 120)

Now,

x2 – 22x + 120 = x2 – 10x – 12x  + 120

= x( x – 10) – 12( x – 10)

= (x – 10) (x – 12)

Hence, x3 – 23x2 + 142x – 120 = (x – 1) (x – 10) (x – 12

The document RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics is a part of the Class 9 Course RD Sharma Solutions for Class 9 Mathematics.
All you need of Class 9 at this link: Class 9
91 docs
Join Course for Free

Top Courses for Class 9

FAQs on RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics

1. What is the importance of factorizing polynomials?
Ans. Factorizing polynomials is important because it helps us simplify complex expressions and solve equations more easily. It allows us to break down a polynomial into its factors, which are easier to work with and understand. Factorization also helps in finding the roots or zeros of a polynomial equation.
2. How can we determine if a polynomial is factorizable?
Ans. A polynomial can be factorized if it can be expressed as a product of two or more polynomials. To determine if a polynomial is factorizable, we can use various techniques such as checking for common factors, using synthetic division, or applying factor theorem. If we can find any factors of the given polynomial, then it is factorizable.
3. What is the process of factorizing a polynomial?
Ans. The process of factorizing a polynomial involves breaking it down into its factors. This can be done by using various techniques such as grouping, finding common factors, applying difference of squares, using the quadratic formula, or using long division. The goal is to express the polynomial as a product of simpler polynomials or binomials.
4. Can all polynomials be factorized?
Ans. No, not all polynomials can be factorized. Some polynomials may not have any factors other than 1 and itself, making them prime polynomials. For example, the polynomial x^2 + 1 cannot be factorized further. However, most polynomials can be factorized using appropriate techniques.
5. How does factorization help in solving polynomial equations?
Ans. Factorization helps in solving polynomial equations by simplifying the expressions and allowing us to find the roots or zeros of the equation. Once a polynomial is factorized, we can set each factor equal to zero and solve for the variables. The solutions to these simpler equations give us the values of the variables that satisfy the original polynomial equation.
Related Exams
About this Document
4.72/5 Rating
Dec 28, 2024 Last updated
Document Description: RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths for Class 9 2024 is part of RD Sharma Solutions for Class 9 Mathematics preparation. The notes and questions for RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths have been prepared according to the Class 9 exam syllabus. Information about RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths covers topics like and RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Example, for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths.
Introduction of RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths in English is available as part of our RD Sharma Solutions for Class 9 Mathematics for Class 9 & RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths in Hindi for RD Sharma Solutions for Class 9 Mathematics course. Download more important topics related with notes, lectures and mock test series for Class 9 Exam by signing up for free. Class 9: RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics - Class 9 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 9 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths
In this doc you can find the meaning of RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths defined & explained in the simplest way possible. Besides explaining types of RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths tests, examples and also practice Class 9 tests
Explore Courses for Class 9 exam

Top Courses for Class 9

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Free

,

RD Sharma Solutions Ex-6.5

,

Viva Questions

,

Extra Questions

,

practice quizzes

,

Important questions

,

MCQs

,

Exam

,

Objective type Questions

,

Maths | RD Sharma Solutions for Class 9 Mathematics

,

Sample Paper

,

RD Sharma Solutions Ex-6.5

,

(Part -1)

,

shortcuts and tricks

,

past year papers

,

ppt

,

Maths | RD Sharma Solutions for Class 9 Mathematics

,

pdf

,

(Part -1)

,

(Part -1)

,

Semester Notes

,

mock tests for examination

,

Class 9

,

Class 9

,

Summary

,

video lectures

,

Class 9

,

Factorization Of Polynomials

,

Factorization Of Polynomials

,

Factorization Of Polynomials

,

study material

,

Maths | RD Sharma Solutions for Class 9 Mathematics

,

RD Sharma Solutions Ex-6.5

,

Previous Year Questions with Solutions

;
Additional Information about RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths for Class 9 Preparation

RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Free PDF Download

The RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths is an invaluable resource that delves deep into the core of the Class 9 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths now and kickstart your journey towards success in the Class 9 exam.

Importance of RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths

The importance of RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths cannot be overstated, especially for Class 9 aspirants. This document holds the key to success in the Class 9 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Notes

RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Notes on EduRev are your ultimate resource for success.

RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Class 9 Questions

The "RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths on the App

Students of Class 9 can study RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RD Sharma Solutions Ex-6.5, (Part -1), Factorization Of Polynomials, Class 9, Maths is prepared as per the latest Class 9 syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup