Ex - 8.1, Linear Equations in One Variable, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Verify by substitution that:
(i) x = 4 is the root of 3x − 5 = 7
(ii) x = 3 is the root of 5 + 3x = 14
(iii) x = 2 is the root of 3x − 2 = 8x − 12
(iv) x = 4 is the root of 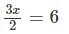
(v) y = 2 is the root of y − 3 = 2y − 5
(vi) x = 8 is the root of 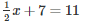
Answer 1:
(i) x = 4 is the root of 3x − 5 = 7.
Now, substituting x = 4 in place of 'x' in the given equation 3x − 5 = 7,
3(4) − 5 = 7
12 − 5 = 7
7 = 7
LHS = RHS
Hence, x = 4 is the root of 3x − 5 = 7.
(ii) x = 3 is the root of 5 + 3x = 14.
Now, substituting x = 3 in place of 'x' in the given equation 5 + 3x = 14,
5 + 3(3) = 14
5 + 9 = 14
14 = 14
LHS = RHS
Hence, x = 3 is the root of 5 + 3x = 14.
(iii) x = 2 is the root of 3x − 2 = 8x − 12.
Now, substituting x = 2 in place of 'x' in the given equation 3x − 2 = 8x − 12,
3(2) − 2 = 8(2) − 12
6 − 2 = 16 − 12
4 = 4
LHS = RHS
Hence, x = 2 is the root of 3x − 2 = 8x − 12.
(iv) x = 4 is the root of 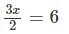
Now, substituting x = 4 in place of 'x' in the given equation 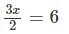
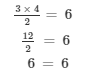
LHS = RHS
Hence, x = 4 is the root of 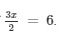
(v) y = 2 is the root of y − 3 = 2y − 5.
Now, substituting y = 2 in place of 'y' in the given equation y − 3 = 2y − 5,
2 − 3 = 2(2) − 5
−1 = 4 − 5
−1 = −1
LHS = RHS
Hence, y = 2 is the root of y − 3 = 2y − 5.
(vi) x = 8 is the root of 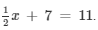
Now, substituting x = 8 in place of 'x' in the given equation 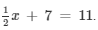
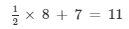
4 + 7 = 11
11 = 11
LHS = RHS
Hence, x = 8 is the root of 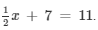
Question 2:
Solve each of the following equations by trial-and-error method:
(i) x + 3 = 12
(ii) x − 7 = 10
(iii) 4x = 28
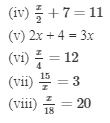
Answer 2:
(i) x + 3 = 12
Here, LHS = x + 3 and RHS = 12.
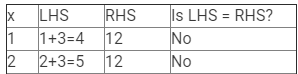
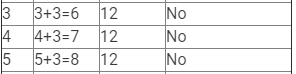
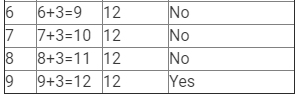
Therefore, if x = 9, LHS = RHS.
Hence, x = 9 is the solution to this equation.
(ii) x − 7 = 10
Here, LHS = x −7 and RHS =10.


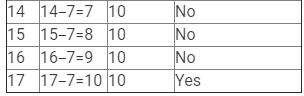
Therefore, if x = 17, LHS = RHS.
Hence, x = 17 is the solution to this equation.
(iii) 4x = 28
Here, LHS = 4x and RHS = 28.
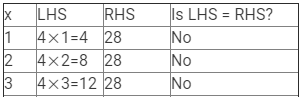
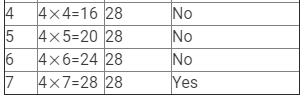
Therefore, if x = 7, LHS = RHS.
Hence, x = 7 is the solution to this equation.
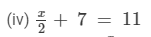
Here, LHS = 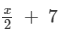 and RHS = 11.
and RHS = 11.
Since RHS is a natural number, x/2 must also be a natural number, so we must substitute values of x that are multiples of 2.


Therefore, if x = 8, LHS = RHS.
Hence, x = 8 is the solution to this equation.
(v) 2x + 4 = 3x
Here, LHS = 2x + 4 and RHS = 3x.


Therefore, if x = 4, LHS = RHS.
Hence, x = 4 is the solution to this equation.
(vi) x/4 = 12
Here, LHS =x/4 and RHS = 12.
Since RHS is a natural number, x/4 must also be a natural number, so we must substitute values of x that are multiples of 4.
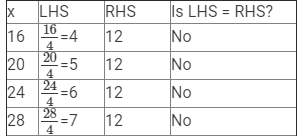
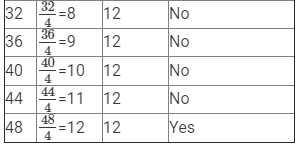
Therefore, if x = 48, LHS = RHS.
Hence, x = 48 is the solution to this equation.
(vii) 15/x = 3
Here, LHS =15/x and RHS = 3.
Since RHS is a natural number, 15/x must also be a natural number, so we must substitute values of x that are factors of 15.
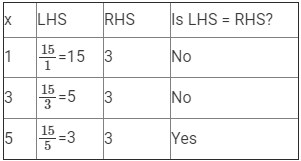
Therefore, if x = 5, LHS = RHS.
Hence, x = 5 is the solution to this equation.
(viii) x/18= 20
Here, LHS =x/18 and RHS = 20.
Since RHS is a natural number, x/18 must also be a natural number, so we must substitute values of x that are multiples of 18.
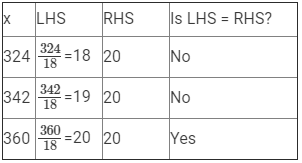
Therefore, if x = 360, LHS = RHS.
Hence, x = 360 is the solution to this equation.
FAQs on Ex - 8.1, Linear Equations in One Variable, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are linear equations in one variable? |  |
| 2. How do you solve linear equations in one variable? |  |
| 3. Can linear equations in one variable have more than one solution? |  |
| 4. What is the importance of linear equations in one variable? |  |
| 5. How can linear equations in one variable be represented graphically? |  |






















