Ex - 8.3, Linear Equations in One Variable, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
Solve each of the following equations. Also, verify the result in each case.
6x + 5 = 2x + 17
Answer 1:
We have
⇒ 6x + 5 = 2x + 17
Transposing 2x to LHS and 5 to RHS, we get
⇒ 6x −- 2x = 17 −- 5
⇒ 4x = 12
Dividing both sides by 4, we get
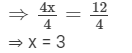
Verification:
Substituting x =3 in the given equation, we get
6××3 + 5 = 2××3 + 17
18 + 5 = 6 + 17
23 = 23
LHS = RHS
Hence, verified.
Question 2:
Solve each of the following equations. Also, verify the result in each case.
2(5x − 3) − 3(2x − 1) = 9
Answer 2:
We have
⇒2(5x − 3) − 3(2x − 1) = 9
Expanding the brackets, we get
⇒ 2×5x − 2×3 −3×2x + 3×1 = 92×5x - 2×3 -3×2x + 3×1 = 9
⇒ 10x − 6 − 6x + 3 = 9
⇒ 10x − 6x − 6 + 3 = 9
⇒ 4x − 3 = 9
Adding 3 to both sides, we get
⇒ 4x − 3 + 3= 9 + 3
⇒ 4x = 12
Dividing both sides by 4, we get
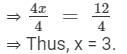
Verification:
Substituting x =3 in LHS, we get
=2(5××3 − 3) − 3(2××3 − 1)
=2××12 − 3 ×× 5
=24 − 15
= 9
LHS = RHS
Hence, verified.
Question 3:
Solve each of the following equations. Also, verify the result in each case.
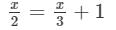
Answer 3:
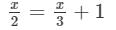
Transposing x/3 to LHS, we get
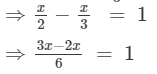
X/6 =1
Multiplying both sides by 6, we get
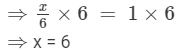
Verification:
Substituting x = 6 in the given equation, we get
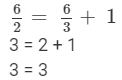
LHS = RHS
Hence, verified.
Question 4:
Solve each of the following equations. Also, verify the result in each case.
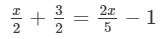
Answer 4:
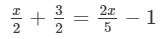
Transposing 2x/5 to LHS and 3/2 to RHS, we get
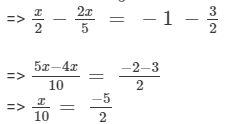
Multiplying both sides by 10, we get
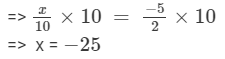
Verification:
Substituting x = −25 in the given equation, we get
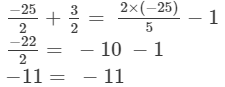
LHS = RHS
Hence, verified.
Question 5:
Solve each of the following equations. Also, verify the result in each case.
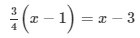
Answer 5:
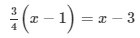
On expanding the brackets on both sides, we get
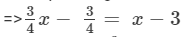
Transposing 3/4x to RHS and 3 to LHS, we get
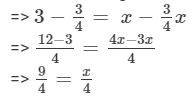
Multiplying both sides by 4, we get
=> x = 9
Verification:
Substituting x = 9 on both sides, we get
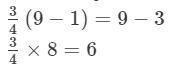
6=6
LHS = RHS
Hence, verified.
Question 6:
Solve each of the following equations. Also, verify the result in each case.
3(x − 3) = 5(2x + 1)
Answer 6:
6. 3(x − 3) = 5(2x + 1)
On expanding the brackets on both sides, we get
=> 3×x − 3×3 = 5×2x + 5×13×x - 3×3 = 5×2x + 5×1
=> 3x −- 9 = 10x + 5
Transposing 10x to LHS and 9 to RHS, we get
=> 3x −- 10x = 9 + 5
=> −-7x = 14
Dividing both sides by 7, we get
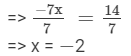
Verification:
Substituting x = −-2 on both sides, we get
3(−2−3) = 5(2(−2) +1)3-2-3 = 52-2 +1
3(−5) = 5(−3)3-5 = 5-3
−-15 = −-15
LHS = RHS
Hence, verified.
Question 7:
Solve each of the following equations. Also, verify the result in each case.
3x − 2 (2x − 5) = 2(x + 3) − 8
Answer 7:
3x − 2 (2x − 5) = 2(x + 3) − 8
On expanding the brackets on both sides, we get
=> 3x−2×2x+2×5 = 2×x + 2×3 −8
=> 3x −4x + 10 = 2x + 6 −8
=> −x + 10 = 2x − 2
Transposing x to RHS and 2 to LHS, we get
=> 10 + 2 = 2x + x
=> 3x = 12
Dividing both sides by 3, we get
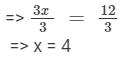
Verification:
Substituting x = 4 on both sides, we get
3(4) − 2(2(4)−5) = 2(4+3)−834 - 224-5 = 24+3-8
12−-2 (8 −- 5) = 14−-8
12 −- 6 = 6
6 = 6
LHS = RHS
Hence, verified.
Question 8:
Solve each of the following equations. Also, verify the result in each case.
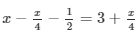
Answer 8:
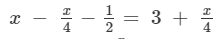
Transposing x/4 to LHS and −1/2 to RHS, we get
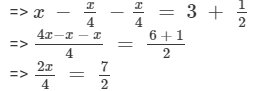
Multiplying both sides by 4, we get
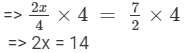
Dividing both sides by 2, we get
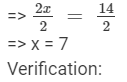
Substituting x = 7 on both sides, we get
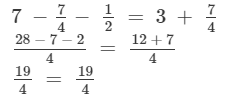
LHS = RHS
Hence, verified.
Question 9:
Solve each of the following equations. Also, verify the result in each case.
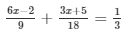
Answer 9:
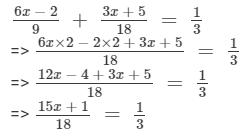
Multiplying both sides by 18, we get
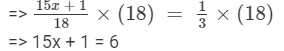
Transposing 1 to RHS, we get
=> 15x = 6−-1
=> 15x = 5
Dividing both sides by 15, we get
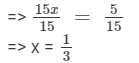
Verification:
Substituting x = 1/3 on both sides, we get
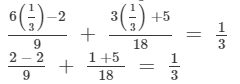
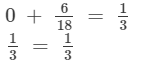
LHS = RHS
Hence, verified.
Question 10:
Solve each of the following equations. Also, verify the result in each case.
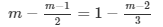
Answer 10:
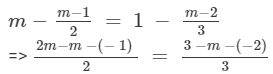
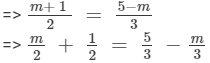
Transposing m/3 to LHS and 1/2 to RHS, we get
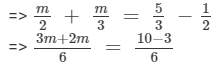
Multiplying both sides by 6, we get
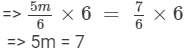
Dividing both sides by 5, we get
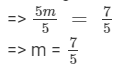
Verification:
Substituting m =7/5 on both sides, we get
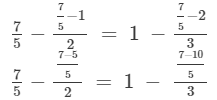
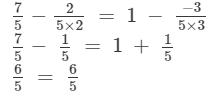
LHS = RHS
Hence, verified.
Question 11:
Solve each of the following equations. Also, verify the result in each case.
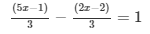
Answer 11:
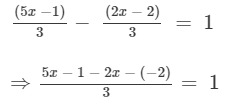
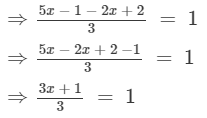
Multiplying both sides by 3, we get
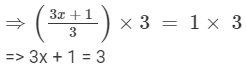
Subtracting 1 from both sides, we get
=> 3x + 1 − 1 = 3 −1
=> 3x = 2
Dividing both sides by 3, we get
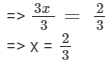
Verification:
Substituting x =2/3 in LHS, we get
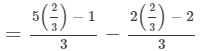

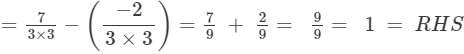
LHS = RHS
Hence, verified.
Question 12:
Solve each of the following equations. Also, verify the result in each case.
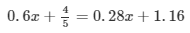
Answer 12:
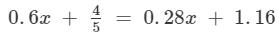
Transposing 0.28x to LHS and 4/5 to RHS, we get
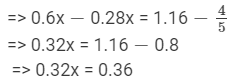
Dividing both sides by 0.32, we get
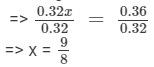
Verification:
Substituting x = 9/8 on both sides, we get
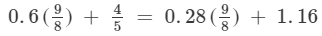
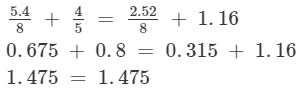
LHS = RHS
Hence, verified.
Question 13:
Solve ech of the following question. Also, verify the result in each case.
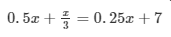
Answer 13:
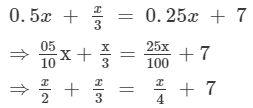
Transposing x/4 to LHS, we get
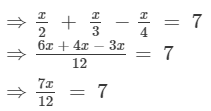
Multiplying both sides by 12, we get
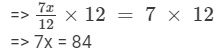
Dividing both sides by 7, we get
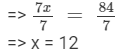
Verification:
Substituting x = 12 on both sides, we get
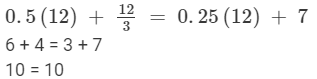
LHS =RHS
Hence, verified.
FAQs on Ex - 8.3, Linear Equations in One Variable, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are linear equations in one variable? |  |
| 2. How do you solve linear equations in one variable? |  |
| 3. Can linear equations in one variable have multiple solutions? |  |
| 4. What is the importance of linear equations in one variable? |  |
| 5. Can linear equations in one variable have no solution? |  |





















