RD Sharma Solutions Ex-8.4, (Part -2), Lines And Angles, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 15 : In the below fig, ∠1 = 60∘ and ∠2 = (2/3)rd of a right angle. Prove that l|| m.
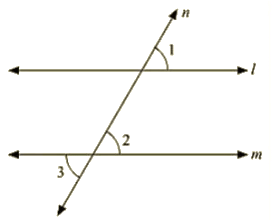
Ans: Given :
∠1 = 60∘ and ∠2 = (2/3)rd of a right angle
To prove: parallel Drawn to m
Proof: ∠1 = 60
∠2 = (23)×90 = 60
Since ∠1 =∠2 = 60∘
Therefore, Parallel to m as pair of corresponding angles are equal.
16. In the below fig, if l||m||n and ∠1 = 60∘. Find ∠2.
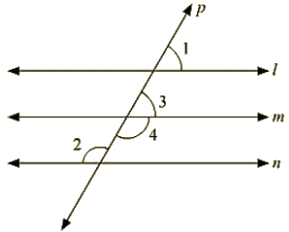
Ans: Since l parallel to m and p is the transversal
Therefore, Given: l || m || n
∠1 = 60∘
To find: ∠2
Sol: ∠1=∠3 = 60∘ [Corresponding angles]
Now, ∠3 and∠4 are linear pair of angles
Therefore, ∠3+∠4 = 180∘
60 + ∠4 = 180
∠4 = 180 — 60
⇒ 120 degree
Also, m||n and P is the transversal
Therefore ∠4 = ∠2 = 120 (Alternative interior angle]
Hence ∠2 = 120 degree
Q 17 : Prove that the straight lines perpendicular to the same straight line are parallel to one another.
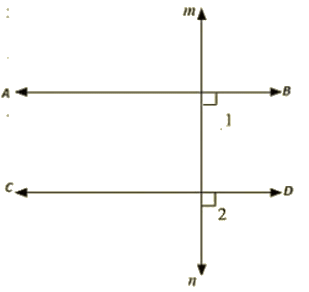
Ans: Let AB and CD be drawn perpendicular to the Line MN
∠ABD = 90∘ [ AB is perpendicular to MN ] —–(i)
∠CON = 90∘ [CD is perpendicular to MN ] —–(ii)
Now,
∠ABD = ∠CDN = 90∘ [From (i) and (ii)]
Therefore, AB||CD, Since corresponding angles are equal.
Q 18 : The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 601. Find the other angles.
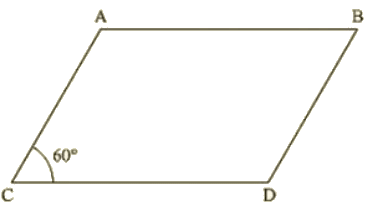
Ans : Given: AB || CD
AD|| BC
Sol: Since AB || CD and AD is the transversal
Therefore, A + D = 180 (Co-interior angles are supplementary)
60 + D = 180
D = 180 – 60
D = 120
Now. AD || BC and AB is the transversal
A + B = 180 degree (Co-interior angles are supplementary)
60 degree +B = 180 degree
B = 180 degree — 60 degree
= 120
Hence, ∠A = ∠C = 60 degree and ∠B =∠D = 120 degree
Q 19: Two lines AB and CD intersect at O. If ∠AOC+∠COB+∠BOD = 270∘, find the measures of ∠AOC,∠COB,∠BOD,∠DOA
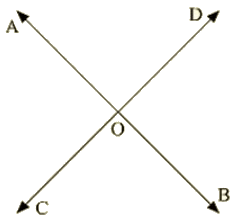
Ans:
Given: ∠AOC+∠COB+∠BOD=270 degree
To find: ∠AOC,∠COB,∠BOD,∠DOA
Here, ∠AOC+∠COB+∠BOD = 270∘ [ Complete angle]
⇒ 270 + AOD = 360
⇒ AOD = 360 — 270
⇒ AOD = 90
Now, AOD + BOD = 180 [Linear pair]
90 + BOD = 180 degree
⇒ BOD = 180 – 90
⇒ BOD = 90 degree
AOD = BOC = 90 degrees [Vertically opposite angles]
BOD = AOC = 90 degrees [Vertically opposite angles]
Q 20. In the below figure, p is a transversal to lines m and n, ∠2 = 120∘ and ∠5 = 60∘. Prove that m|| n.
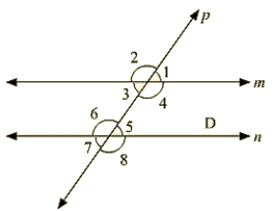
Ans :
Given: ∠2 = 120∘ and ∠5 = 60∘
To prove: ∠2+∠1 = 180∘ [ Linear pair ]
120+∠1 = 180 degree
∠1 = 180−120 degree
∠1 = 60 degree
Since ∠1 = ∠5 = 60 degree
Therefore, m||n [As pair of corresponding angles are equal]
Q 21: In the below fig. transversal "t intersects two lines m and n, ∠4 =110∘ and ∠7 = 65∘ Is m||n?
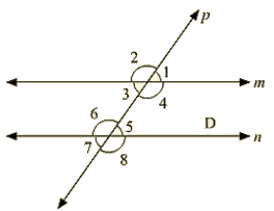
Ans: Given :
∠4 = 110∘ and ∠7 = 65∘
To find: Is m||n
Here ∠7 = ∠5 = 65∘ [Vertically opposite angle]
Now. ∠4+∠5 = 110+65 = 175∘
Therefore, m is not parallel to n as the pair of co-interior angles is not supplementary.
Q 22: Which pair of lines in the below fig. is parallel? give reasons.
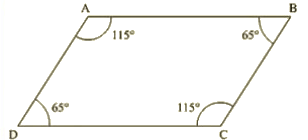
Ans : ∠A+∠B = 115+65 = 180∘
Therefore, AB || BC [ As the sum of co-interior angles are supplementary]
∠B+∠C = 65+115 = 180∘
Therefore, AB || CD (As the sum of interior angles are supplementary]
Q 23: If I, m, n are three lines such that I|| m and n are perpendicular to l, prove that n is perpendicular to m.
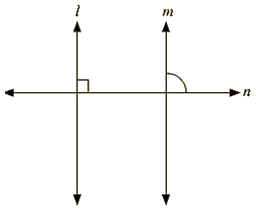
Ans :
Given, l||m, n perpendicular to I
To prove: n perpendicular to m
Since l||m and n intersect
∴ ∠1 = ∠2 [Corresponding angles]
But, U = 90
⇒ ∠2 = 90∘
Hence n is perpendicular to m
Q 24: In the below fig, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of∠DEF. Prove that ∠ABC = ∠DEF.
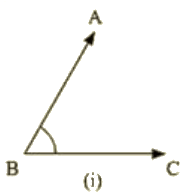
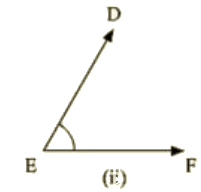
Ans:
Given: AB || DE and BC || EF
To prove: ∠ABC=∠DEF
Construction:Construction: Produce BC to x such that it intersects DE at M.
Proof: Since AB || DE and BX is the transversal
ABC = DMX [Corresponding angle] —–(i)
Also, BX || EF and DE Is the transversal
DMX = DEF [Corresponding angles] —–(ii)
From (i) and (ii)
∠ABC =∠DEF
Q 25: In the below fig, arms BA and BC of ABC are respectively parallel to arms ED and EF of DEF Prove that ∠ABC+∠DEP = 180∘
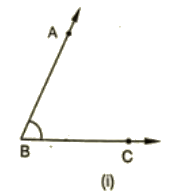

Ans :
Given: AB II DE, BC II EF
To prove: ∠ABC+∠DEF = 180∘
Construction: Produce BC to intersect DE at M
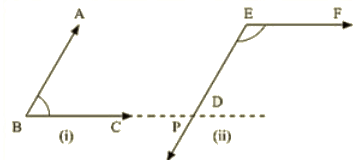
Proof :
Since AB || EM and BL is the transversal
∠ABC = ∠EML [Corresponding angle] —–(i)
Also,
EF || ML and EM is the transversal
By the property of co-interior angles are supplementary
∠DEF+∠EML = 180∘ (ii)
From (i) and (ii) we have
Therefore ∠DEF+∠ABC = 180∘
Q 26 : With of the following statements are true (T) and which are false (F)? Give reasons.
(1) If two lines are intersected by a transversal, then corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
(ii) Two lines perpendicular to the same line are perpendicular to each other.
(iv) Two lines parallel to the same line are parallel to each other.
(v) If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are equal.
Ans :
(i) False
(ii)True
(iii) False
(iv) True
(v) False
Q 27: Fill in the blanks in each of the following to make the statement true:
(i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are ____________
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are _____________
(iii) Two lines perpendicular to the same line are _______ to each other
(Iv) Two lines parallel to the same line are __________ to each other.
(v) If a transversal intersects a pair of lines in such a way that a pair of alternate angles we equal. then the lines are ___________
(vi) If a transversal intersects a pair of lines in such a way that the sum of interior angles on the seine side of transversal is 180′. then the lines are _____________
Ans :
(i) Equal
(ii) Parallel
(iii) Supplementary
(iv) Parallel
(v) Parallel
(vi) Parallel
FAQs on RD Sharma Solutions Ex-8.4, (Part -2), Lines And Angles, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the different types of angles? |  |
| 2. How can we determine if two lines are parallel? |  |
| 3. What is the sum of the angles of a triangle? |  |
| 4. How can we find the measure of an angle using a protractor? |  |
| 5. What is the difference between a line segment and a ray? |  |
















