Ex - 8.4, Linear Equations in One Variable, Class 7, Math RD Sharma Solutions | RD Sharma Solutions for Class 7 Mathematics PDF Download
Question 1:
If 5 is subtracted from three times a number, the result is 16. Find the number.
Answer 1:
Let the required number be 'x'. Then, 5 subtracted from 3 times x = 3x −- 5.
⇒ 3x −5 = 16
Adding 5 to both sides, we get
⇒ 3x − 5 + 5 = 16 + 5
⇒ 3x= 21
Dividing both sides by 3, we get
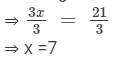
Thus, the required number is 7.
Question 2:
Find the number which when multiplied by 7 is increased by 78.
Answer 2:
Let the required number be 'x'. Thus, when multiplied by 7, it gives 7x, and x increases by 78.
⇒ 7x = x + 78
Transposing x to LHS, we get
⇒ 7x − x = 78
⇒ 6x = 78
Dividing both sides by 6, we get
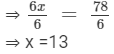
Thus, the required number is 13.
Question 3:
Find three consecutive natural numbers such that the sum of the first and second is 15 more than the third.
Answer 3:
Let the first number be 'x'. Hence, the second number = x + 1 and the third number = x + 2.
⇒ Sum of first and second numbers = (x) + (x + 1).
ATQ:
⇒ (x) + (x + 1) = 15 + (x + 2)
⇒ 2x + 1 = 17 + x
Transposing x to LHS and 1 to RHS, we get
⇒ 2x − x = 17 − 1
⇒ x = 16
So, first number = x = 16
Second number = x + 1 = 16 + 1 = 17
Third number = x + 2 = 16 + 2 = 18
Thus, the required consecutive natural numbers are 16, 17 and 18.
Question 4:
The difference between two numbers is 7. Six times the smaller plus the larger is 77. Find the numbers.
Answer 4:
Let the smaller number be 'x'. So, the larger number = x + 7.
ATQ:
⇒ 6x + (x + 7) = 77
⇒ 6x + x + 7 = 77
⇒ 7x + 7 = 77
Subtracting 7 from both sides, we get
⇒ 7x + 7 − 7 = 77 − 7
⇒ 7x = 70
Dividing both sides by 7, we get
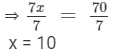
Thus, the smaller number = x = 10, and the larger number = x + 7 = 10 + 7 = 17.
The two required numbers are 10 and 17.
Question 5:
A man says, "I am thinking of a number. When I divide it by 3 and then add 5, my answer is twice the number I thought of". Find the number.
Answer 5:
Let the number thought of by the man be 'x'.
So, ATQ:
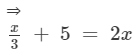
Transposing x/3 to RHS, we get
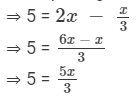
Multiplying both sides by 3, we get
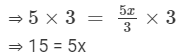
Dividing both sides by 5, we get
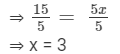
Thus, the number thought of by the man is 3.
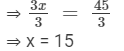
Question 6:
If a number is tripled and the result is increased by 5, we get 50. Find the number.
Answer 6:
Let the required number be 'x'.
So, ATQ:
⇒ 3x + 5 = 50
Subtracting 5 from both sides, we get
⇒ 3x + 5 − 5 = 50 − 5
⇒ 3x = 45
Dividing both sides by 3, we get
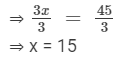
Thus, the required number is 15.
Question 7:
Shikha is 3 years younger to her brother Ravish. If the sum of their ages is 37 years, what are their present ages?
Answer 7:
Let the present age of Shikha = 'x' years.
So, the present age of Shikha's brother Ravish = (x + 3) years.
So, sum of their ages = x + (x+ 3)
⇒ x + ( x + 3 ) = 37
⇒ 2x + 3 = 37
Subtracting 3 from both sides, we get
⇒ 2x + 3 −- 3 = 37 −- 3
⇒ 2x = 34
Dividing both sides by 2, we get
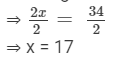
So, the present age of Shikha = 17 years, and the present age of Ravish = x+ 3 = 17 + 3 = 20 years.
Question 8:
Mrs. Jain is 27 years older than her daughter Nilu. After 8 years she will be twice as old as Nilu. Find their present ages.
Answer 8:
Let the present age of Nilu = 'x' years.
Therefore, the present age of Nilu's mother, Mrs. Jain = (x + 27) years.
So, after 8 years,
Nilu's age = (x + 8), and Mrs. Jain's age = (x + 27 + 8) = (x + 35) years
⇒ x + 35 = 2(x + 8)
Expanding the brackets, we get
⇒ x + 35 = 2x + 16
Transposing x to RHS and 16 to LHS, we get
⇒ 35 −- 16 = 2x −- x
⇒ x = 19
So, the present age of Nilu = x = 19 years, and the present age of Nilu's mother = x+ 27 = 19 + 27 = 46 years.
Question 9:
A man is 4 times as old as his son. After 16 years, he will be only twice as old as his son. Find the their present ages.
Answer 9:
Let the present age of the son = 'x' years.
Therefore, the present age of his father = '4x' years.
So, after 16 years,
Son's age = (x + 16) and father's age = (4x + 16) years
ATQ:
⇒ 4x + 16 = 2(x + 16)
⇒ 4x + 16 = 2x + 32
Transposing 2x to LHS and 16 to RHS, we get
⇒ 4x - 2x = 32 - 16
⇒ 2x = 16
Dividing both sides by 2, we get
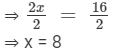
So, the present age of the son = x = 8 years, and the present age of the father = 4x = 4(8) = 32 years.
Question 10:
The difference in age between a girl and her younger sister is 4 years. The younger sister in turn is 4 years older than her brother. The sum of the ages of the younger sister and her brother is 16. How old are the three children?
Answer 10:
Let the age of the girl = 'x' years.
So, the age of her younger sister = (x − 4) years.
Thus, the age of the brother = (x −1 4 − 4) years = (x − 8) years.
ATQ:
⇒ (x −- 4) + (x −- 8) = 16
⇒ x + x −- 4 −- 8 = 16
⇒ 2x −- 12 = 16
Adding 12 to both sides, we get
⇒ 2x −- 12 + 12 = 16 + 12
⇒ 2x = 28
Dividing both sides by 2, we get
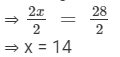
Thus, the age of the girl = x = 14 years, the age of the younger sister = x −- 4 = 14 −- 4 = 10 years,
and the age of the younger brother = x −- 8 = 14 −- 8 = 6 years.
Question 11:
One day, during their vacation at a beach resort, Shella found twice as many sea shells as Anita and Anita found 5 shells more than sandy. Together sandy and Shella found 16 sea shells. How many did each of them find?
Answer 11:
Let the number of sea shells found by Sandy = 'x'.
So, the number of sea shells found by Anita = (x + 5).
The number of sea shells found by Shella = 2 (x + 5 ).
According to the question,
⇒ x + 2 (x + 5) = 16
⇒ x + 2x + 10 = 16
⇒ 3x + 10 = 16
Subtracting 10 from both sides, we get
⇒ 3x + 10 −- 10 = 16 −- 10
⇒ 3x = 6
Dividing both sides by 3, we get
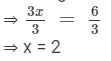
Thus, the number of sea shells found by Sandy = x = 2, the number of sea shells found by Anita = x + 5 = 2 + 5 = 7,
and the number of sea shells found by Shella = 2(x + 5) = 2(2 + 5) = 2(7 ) = 14.
Question 12:
Andy has twice as many marbles as Pandy, and Sandy has half as many has Andy and Pandy put together. Andy has 110 marbles which is 115 marbles less than Sandy. How many does each of them have?
Answer 12:
Let the number of marbles with Pandy = 'x'.
So, the number of marbles with Andy = '2x'.
Thus, the number of marbles with Sandy = 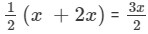
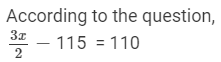
Adding 115 to both sides, we get
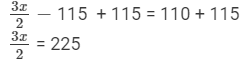
Multiplying both sides by 2, we get
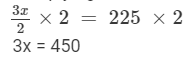
Dividing both sides by 3, we get
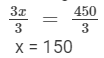
So, Pandy has 150 marbles, Andy has 2x = 2(150) = 300 marbles, and Sandy has 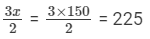 marbles.
marbles.
Question 13:
A bag contains 25 paise and 50 paise coins whose total value is Rs 30. If the number of 25 paise coins is four times that of 50 paise coins, find the number of each type of coins.
Answer 13:
Let the number of 50 paise coins = 'x'.
So, the money value contribution of 50 paise coins = 0.5x.
The number of 25 paise coins = '4x'.
The money value contribution of 25 paise coins = 0.25(4x) = x.
According to the question,
⇒ 0.5x + x = 30
⇒ 1.5x = 30
Dividing both sides by 1.5, we get

Thus, the number of 50 paise coins = 'x' = 20, and the number of 25 paise coins = '4x' = 4 (20) = 80.
Question 14:
The length of a rectangular field is twice its breadth. If the perimeter of the field is 228 metres, find the dimensions of the field.
Answer 14:
Let the breadth of the rectangle = 'x' metres.
According to the question,
Length of the rectangle = '2x' metres
Perimeter of a rectangle = 2 (length + breadth)
So, 2 (2x + x) = 228
=> 2 (3x) = 228
=> 6x = 228
Dividing both sides by 6, we get
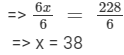
So, the breadth of the rectangle = x = 38 metres, and the length of the rectangle = 2x = 2(38) = 76 metres.
Question 15:
There are only 25 paise coins in a purse. The value of money in the purse is Rs 17.50. Find the number of coins in the purse.
Answer 15:
Let the number of 25-paise coins in the purse be 'x'.
So, the value of money in the purse = 0.25x.
But 0.25x = 17.5.
Dividing both sides by 0.25, we get
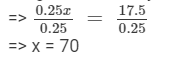
Thus, the number of 25-paise coins in the purse = 70.
Question 16:
In a hostel mess, 50 kg rice are consumed everyday. If each student gets 400 gm of rice per day, find the number of students who take meals in the hostel mess.
Answer 16:
Let the number of students in the hostel be 'x'.
Quantity of rice consumed by each student = 400 gm.
So, daily rice consumption in the hostel mess = 400(x).
But, daily rice consumption = 50 kg = 50 ×× 1000 = 50000 gm [since 1 kg = 1000 gm].
According to the question,
400x = 50000
Dividing both sides by 400, we get
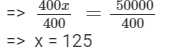
Thus, 125 students have their meals in the hostel mess.
FAQs on Ex - 8.4, Linear Equations in One Variable, Class 7, Math RD Sharma Solutions - RD Sharma Solutions for Class 7 Mathematics
| 1. What are linear equations in one variable? |  |
| 2. How do you solve linear equations in one variable? |  |
| 3. Can a linear equation in one variable have multiple solutions? |  |
| 4. What is the importance of linear equations in one variable? |  |
| 5. Can a linear equation in one variable have no solution? |  |






















