Ex-9.1, Triangle And Its Angles, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1) InaΔABC,if∠A = 550,∠B = 400,Find∠C.
Solution:
Given Data:
∠B = 550,∠B = 400,then∠C = ?
We know that
InaΔABC sum of all angles of a triangle is 1800
i.e., ∠A+∠B+∠C = 1800
⇒ 550+400+∠C = 1800
⇒ 950+∠C = 1800
⇒ ∠C = 1800−950
⇒ ∠C = 850
Q2) If the angles of a triangle are in the ratio 1:2:3, determine three angles.
Solution:
Given that,
Angles of a triangle are in the ratio 1:2:3
Let the angles be x, 2x, 3x
∴ We know that,
Sum of all angles of triangles is 1800
x+2x+3x = 1800
⇒ 6x = 1800
⇒ x = 
⇒ x = 300
Since x = 300
2x = 2(30)0 = 600
3x = 3(30)0 = 900
Therefore, angles are 300, 600, 900
Q3) The angles of a triangle are (x−400),(x−200)and( x−100). Find the value of x.
x−100). Find the value of x.
Solution:
Given that,
The angles of a triangle are
(x−400),(x−200)and( x−100)
x−100)
We know that,
Sum of all angles of triangle is 1800
∴(x−400)+(x−200)+( x−100) = 1800
x−100) = 1800
2x+ x−700 = 1800
x−700 = 1800
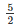 x = 1800+700
x = 1800+700
5x = 2(250)0
x = 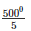
∴x = 1000
Q4) The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is 100, find the three angles.
Solution:
Given that,
The difference between two consecutive angles is 100
Let x, x+100, x+200 be the consecutive angles that differ by 100
We know that,
Sum of all angles in a triangle is 1800
x+x+100+x+200 = 1800
3x+300 = 1800
⇒ 3x = 1800– 300
⇒ 3x = 1500
⇒ x = 500
Therefore, the required angles are
x = 500
x+100 = 500 + 100 = 600
x+200 = 500 + 200 = 700
As the difference between two consecutive angles is 100, the three angles are 500,600,700.
Q5) Two angles of a triangle are equal and the third angle is greater than each of those angles by 300. Determine all the angles of the triangle.
Solution:
Given that,
Two angles of a triangle are equal and the third angle is greater than each of those angles by 300.
Let x, x, x+300 be the angles of a triangle
We know that,
Sum of all angles in a triangle is 1800
x + x + x + 300 = 1800
3x + 300 = 1800
3x = 1800−300
3x = 1500
x = 500
Therefore, the three angles are 500,500,800.
Q6) If one angle of a triangle is equal to the sum of the other two, show that the triangle is a right angle triangle.
Solution:
If one angle of a triangle is equal to the sum of the other two angles
⇒ ∠B = ∠A+∠C
In ΔABC,
Sum of all angles of a triangle is 1800
⇒ ∠A+∠B+∠C = 1800
⇒ ∠B+∠B = 1800[∠ B = ∠ A+∠C]
⇒ 2∠B = 1800
⇒ ∠B = 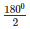
⇒ ∠B = 900
Therefore, ABC is a right angled triangle.
Q7) ABC is a triangle in which ∠A = 720, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC.
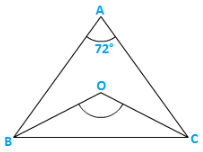
Solution:
Given,
ABC is a triangle where ∠A = 720 and the internal bisector of angles B and C meeting O.
In ΔABC,
∠A+∠B+∠C = 1800
⇒ 720+∠B+∠C = 1800
⇒ ∠B+∠C = 1800−720
Dividing both sides by ‘2’
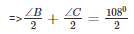
⇒ ∠OBC+∠OCB = 540
Now, InΔBOC⇒ ∠OBC+∠OCB+∠BOC = 1800
⇒ 540+∠BOC = 1800
⇒ ∠BOC = 1800−540 = 1260
∴∠BOC = 1260
Q8) The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Solution:
In ΔXYZ,
Sum of all angles of a triangle is 1800
i.e., ∠X+∠Y+∠Z = 1800
Dividing both sides by ‘2’
⇒  ∠X+
∠X+ ∠Y+
∠Y+ ∠Z = 1800
∠Z = 1800
⇒  ∠X+∠OYZ+∠OYZ = 900 [∵ OY, OZ,∠ Y and ∠ Z]
∠X+∠OYZ+∠OYZ = 900 [∵ OY, OZ,∠ Y and ∠ Z]
⇒ ∠OYZ+∠OZY = 900− ∠X
∠X
Now in ΔYOZ
∴∠YOZ+∠OYZ+∠OZY = 1800
⇒ ∠YOZ+900− ∠X = 1800
∠X = 1800
⇒ ∠YOZ = 900− ∠X
∠X
Therefore, the bisectors of a base angle cannot enclosure right angle.
Q9) If the bisectors of the base angles of a triangle enclose an angle of 1350, prove that the triangle is a right angle.
Solution:
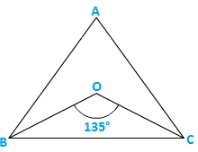
Given the bisectors of the base angles of a triangle enclose an angle of 1350
i.e., ∠BOC = 1350
But, We know that
∠BOC = 900+ ∠A
∠A
⇒ 1350 = 900+ ∠A
∠A
⇒  ∠A = 1350−900
∠A = 1350−900
⇒ ∠A = 450(2)
⇒ ∠A = 900
Therefore, ΔABC is a right angle triangle that is right angled at A.
Q10) In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABCand∠ACB intersect at O such that ∠BOC = 1200. Show that ∠A = ∠B = ∠C = 600.
Solution:
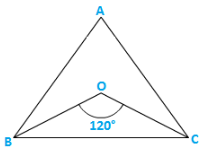
Given,
In ΔABC,
∠ABC = ∠ACB
Dividing both sides by ‘2’
 ∠ABC =
∠ABC =  ∠ACB
∠ACB
⇒ ∠OBC = ∠OCB [∴OB,OC bisects ∠B and ∠C]
Now,
∠BOC = 900+ ∠A
∠A
⇒ 1200−900 =  ∠A
∠A
⇒ 300∗(2) = ∠A
⇒ ∠A = 600
Now in ΔABC
∠A+∠ABC+∠ACB = 1800(Sumofallanglesofatriangle)
⇒ 600+2∠ABC = 1800 [∴∠ABC = ∠ACB]
⇒ 2∠ABC = 1800−600
⇒ ∠ABC = 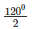 = 600
= 600
⇒ ∠ABC = ∠ACB
∴∠ACB = 600
Hence Proved.
Q11) Can a triangle have:
(i) Two right angles?
(ii) Two obtuse angles?
(iii) Two acute angles?
(iv) All angles more than 60°?
(v) All angles less than 60°?
(vi) All angles equal to 60″?
Justify your answer in each case.
Sol:
(i) No,
Two right angles would up to 180°. So the third angle becomes zero. This is not possible, so a triangle cannot have two right angles. [Since sum of angles in a triangle is 1800]
(ii) No,
A triangle can’t have 2 obtuse angles. Obtuse angle means more than 90° So that the sum of the two sides will exceed 180° which is not possible. As the sum of all three angles of a triangle is 180°.
(iii) Yes
A triangle can have 2 acute angles. Acute angle means less the 90″ angle.
(iv) No
Having angles more than 600 make that sum more than 1800. This is not possible. [Since the sum of all the internal angles of a triangle is 1800]
(v) No
Having all angles less than 600 will make that sum less than 1800 which is not possible.[Therefore, the sum of all the internal angles of a triangle is 1800]
(vi) Yes
A triangle can have three angles equal to 600 . Then the sum of three angles equal to the 1800. Such triangles are called as equilateral triangle. [Since, the sum of all the internal angles of a triangle is1800]
Q12) If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Solution
Given each angle of a triangle less than the sum of the other two
∴∠X+∠Y+∠Z
⇒ ∠X+∠X<∠X+∠Y+∠Z
⇒ 2∠X<1800 [Sumofalltheanglesofatriangle]
⇒ ∠X<900
Similarly ∠Y<900and∠Z<900
Hence, the triangles are acute angled.
FAQs on Ex-9.1, Triangle And Its Angles, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the angles of a triangle? |  |
| 2. How can I find the measure of an angle in a triangle? |  |
| 3. Can a triangle have two right angles? |  |
| 4. How can I classify triangles based on their angles? |  |
| 5. Is it possible for a triangle to have more than one obtuse angle? |  |
















