Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1)
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Without performing actual addition and division write the quotient when the sum of 69 and 96 is divided by
(i) 11
(ii) 15
Answer 1: (i) Clearly, 69 and 96 are two numbers such that one can be obtained be reversing the digits of the other. Therefore, when the sum of 69 and 96 is divided by 11, we get 15 (sum of the digits) as quotient.
(ii) Clearly, 69 and 96 are two numbers such that one can be obtained be reversing the digits of the other. Therefore, when the sum of 69 and 96 is divided by 15 (sum of the digits), we obtain 11 as quotient.
Question 2: Without performing actual computations, find the quotient when 94 − 49 is divided by
(i) 9
(ii) 5
Answer 2: (i) We know that when ab−ba is divided by 9, the quotient is a−b.Therefore, when (94−49) is divided by 9, the quotient is (9−4 = 5).(ii) We know that when ab−ba is divided by (a−b), the quotient is 9.Therefore, when (94−49) is divided by (9−4=5), the quotient is 9.Question 3: If sum of the number 985 and two other numbers obtained by arranging the digits of 985 in cyclic order is divided by 111, 22 and 37 respectively. Find the quotient in each case.
Answer 3: The sum of (985+859+598) when divided by:(i) 111Quotient = (9+8+5)=22(ii) 22, i.e, (9+8+5)Quotient = 111(iii) 37 (= 111/3)Quotient = 3(9+8+5)=66
Question 4: Find the quotient when the difference of 985 and 958 is divided by 9.
Answer 4: If abc-acb is divided by 9, the quotient is (b-c).∴If (985-958) is divided by 9, quotient=(8-5)=3
Question 5: Given that the number ¯¯¯¯¯¯¯¯¯¯ 35α6435α64¯ is divisible by 3, where α is a digit, what are the possible values of α?
Answer 5: It is given that¯¯¯¯¯¯¯¯¯¯¯ 35a64 is a multiple of 3.∴ (3+5+a+6+4) is a multiple of 3.∴ (a+18) is a multiple of 3.∴ (a+18)=0, 3, 6, 9, 12, 15, 18, 21...But a is a digit of number ¯¯¯¯¯¯¯¯¯¯¯¯ 35a64 . So, a can take value 0, 1, 2, 3, 4...9.a+18=18 ⇒a=0a+18=21 ⇒a=3a+18=24 ⇒a=6a+18=27 ⇒a=9∴ a=0, 3, 6, 9
Question 6: If x is a digit such that the number ¯¯¯¯¯¯¯¯¯¯ 18x7118x71¯ is divisible by 3, find possible values of x.
Answer 6: It is given that ¯¯¯¯¯¯¯¯¯¯ 18x71 is a multiple of 3.∴(1+8+x+7+1) is a multiple of 3.∴(17+x) is a multiple of 3.∴17+x=0, 3, 6, 9, 12, 15, 18, 21...But x is a digit. So, x can take values 0,1,2,3,4...9.17+x=18 ⇒x=117+x=21 ⇒x=417+x=24 ⇒x=7x=1,4,7Question 7: If x is a digit of the number ¯¯¯¯¯¯¯¯¯¯¯¯ 66784x66784x¯ such that it is divisible by 9, find possible values of x.
Answer 7: It is given that ¯¯¯¯¯¯¯¯¯¯¯¯¯ 66784x is a multiple of 9.Therefore, (6+6+7+8+4+x) is a multiple of 9.And,(31+x) is a multiple of 9. Possible values of (31+x) are 0, 9, 18, 27, 36, 45,...But x is a digit. So, x can only take value 0, 1, 2, 3, 4,...9.∴31+x=36 ⇒x=36−31⇒x=5
Question 8: Given that the number ¯¯¯¯¯¯¯¯¯¯ 67y1967y19¯ is divisible by 9, where y is a digit, what are the possible values of y?
Answer 8: It is given that ¯¯¯¯¯¯¯¯¯¯ 67y19 is a multiple of 9.∴ (6+7+y+1+9) is a multiple of 9. ∴(23+y) is a multiple of 9. 23+y=0, 9, 18, 27, 36...But x is a digit. So, x can take values 0,1,2,3,4...9.23+y=27⇒y=4 Question 9: If ¯¯¯3x23x2¯ is a multiple of 11, where x is a digit, what is the value of x?
Answer 9: Sum of the digits at odd places = 3+2= 5Sum of the digit at even place = x∴ Sum of the digit at even place−Sum of the digits at odd places=(x−5)∵ (x−5) must be multiple by 11.∴ Possible values of (x−5) are 0, 11, 22, 33...But x is a digit; therefore x must be 0, 1 ,2, 3...9.∴ x−5=0 ⇒x=5
Question 10: If ¯¯¯¯¯¯¯¯ 98215x298215x2¯ is a number with x as its tens digit such that is is divisible by 4. Find all possible values of x.
Answer 10: A natural number is divisible by 4 if the number formed by its digits in units and tens places is divisible by 4.∴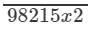
will be divisible by 4 if 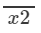is divisible by 4.
will be divisible by 4 if 
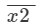is divisible by 4. ∴=10x + 2x is a digit; therefore possible values of x are 0, 1, 2, 3...9.¯¯¯¯¯ x2 =2, 12, 22, 32, 42, 52, 62, 72, 82, 92The numbers that are divisible by 4 are 12, 32, 52, 72, 92.Therefore, the values of x are 1, 3, 5, 7, 9.
=10x + 2Question 11: If x denotes the digit at hundreds place of the number ¯¯¯¯¯¯ 67x1967x19¯ such that the number is divisible by 11. Find all possible values of x.
Answer 11 : A number is divisible by 11, if the difference of the sum of its digits at odd places and the sum of its digits at even places is either 0 or a multiple of 11.Sum of digits at odd places−Sum of digits at even places=(6 + x + 9)−(7 + 1)=(15 + x)−8=x + 7∴ x + 7 =11 ⇒ x = 4
Question 12: Find the remainder when 981547 is divided by 5. Do this without doing actual division.
Answer 12: If a natural number is divided by 5, it has the same remainder when its unit digit is divided by 5.Here, the unit digit of 981547 is 7. When 7 is divided by 5, remainder is 2.Therefore, remainder will be 2 when 981547 is divided by 5.
Question 13: Find the remainder when 51439786 is divided by 3. Do this without performing actual division.
Answer 13: Sum of the digits of the number 51439786 = 5 + 1 + 4 + 3 + 9 + 7 + 8 + 6 = 43
The remainder of 51439786, when divided by 3, is the same as the remainder when the sum of the digits is divided 3.
When 43 is divided by 3, remainder is 1.
Therefore, when 51439786 is divided by 3, remainder will be 1.
Question 14: Find the remainder, without performing actual division, when 798 is divided by 11.
Answer 14: 798 =A multiple of 11 + (Sum of its digits at odd places − Sum of its digits at even places)798 =A multiple of 11 + (7 + 8 − 9)798 =A multiple of 11 + (15 − 9)798 =A multiple of 11 + 6Therefore, the remainder is 6.
Question 15: Without performing actual division, find the remainder when 928174653 is divided by 11.
Answer 15: 928174653= A multiple of 11 + (Sum of its digits at odd places −Sum of its digits at even places)
928174653= A multiple of 11 + {(9 + 8 + 7 + 6 + 3) − (2 + 1 + 4 + 5)}928174653= A multiple of 11 + (33 − 12)928174653= A multiple of 11 + 21928174653= A multiple of 11 + (11 × 1 + 10)928174653= A multiple of 11 + 10Therefore, the remainder is 10.
Question 16: Given an example of a number which is divisible by
(i) 2 but not by 4.
(ii) 3 but not by 6.
(iii) 4 but not by 8.
(iv) both 4 and 8 but not by 32.
Answer 16: (i) 10
Every number with the structure (4n + 2) is an example of a number that is divisible by 2 but not by 4.
(ii) 15
Every number with the structure (6n + 3) is an example of a number that is divisible by 3 but not by 6.
(iii) 28
Every number with the structure (8n + 4) is an example of a number that is divisible by 4 but not by 8.
(iv) 8
Every number with the structure (32n + 8), (32n + 16) or (32n + 24) is an example of a number that is divisible by 4 and 8 but not by 32.
Question 17: Which of the following statements are true?
(i) If a number is divisible by 3, it must be divisible by 9.
(ii) If a number is divisible by 9, it must be divisible by 3.
(iii) If a number is divisible by 4, it must be divisible by 8.
(iv) If a number is divisible by 8, it must be divisible by 4.
(v) A number is divisible by 18, if it is divisible by both 3 and 6.
(vi) If a number is divisible by both 9 and 10, it must be divisible by 90.
(vii) If a number exactly divides the sum of two numbers, it must exactly divide the numbers separately.
(viii) If a number divides three numbers exactly, it must divide their sum exactly.
(ix) If two numbers are co-prime, at least one of them must be a prime number.
(x) The sum of two consecutive odd numbers is always divisible by 4.
Answer 17: (i) False
Every number with the structures (9n + 3) or (9n + 6) is divisible by 3 but not by 9. Example: 3, 6, 12 etc.
(ii) True
(iii) False
Every number with the structure (8n + 4) is divisible by 4 but not by 8. Example: 4, 12, 20 etc.
(iv) True
(v) False
Example: 24 is divisible by both 3 and 6 but it is not divisible by 18.
(vi) True
(vii) False
Example: 5 divides 10, which is a sum of 3 and 7. However, it neither divides 3 nor 7.
(viii) True
(ix) False
Example: 4 and 9 are co-prime numbers but both are composite numbers too.
(x) True
Question 18: Solve each of the following Cryptarithms:
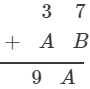
Answer 18:Two possible values of A are:(i) If 7 + B ≤ 9∴ 3 + A = 9 ⇒ A = 6But if A = 6, 7 + B must be larger than 9. Hence, it is impossible.(ii) If 7 + B ≥ 9∴ 1 + 3 + A = 9⇒ A = 5If A = 5 and 7 + B = 5, B must be 8∴ A = 5, B = 8
Question 19: Solve each of the following Cryptarithm:
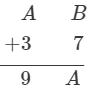
Answer 19: Two possibilities of A are:(i) If B + 7 ≤ 9, A = 6But clearly, if A = 6, B + 7 ≥ 9; it is impossible(ii) If B + 7 ≥ 9, A = 5 and B + 7 = 5 Clearly, B = 8∴ A = 5, B = 8
Question 20: Solve each of the following Cryptarithm:
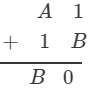
Answer 20: If 1 + B = 0 Surely, B = 9If 1 + A + 1 = 9 Surely, A = 7
Question 21: Solve each of the following Cryptarithm:
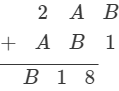
Answer 21: B + 1 = 8, B = 7A + B = 1, A + 7 = 1, A = 4So, A = 4, B = 7
Question 22: Solve each of the following Cryptarithm:
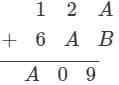
Answer 22: A + B = 9 as the sum of two digits can never be 192 + A = 0, A must be 8A + B = 9, 8 + B = 9, B = 1So, A = 8, B = 1
Question 23: Solve each of the following Cryptarithm:
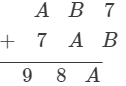
Answer 23: If A + B = 8, A + B ≥ 9 is possible only if A = B = 9But from 7 + B = A, A = B = 9 is impossibleSurely, A + B = 8, A + B ≤ 9So, A + 7 = 9, Surely A = 27 + B = A, 7 + B = 2, B = 5So, A = 2, B = 5
Question 24: Solve each of the following Cryptarithm:
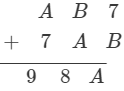
Answer 24: 0 is the only unit digit number, which gives the same 0 at the unit digit when multiplied by 4. So, the possible value of B is 0.Similarly, for A also, 0 is the only possible digit.But then A, B and C will all be 0.And if A, B and C become 0, these numbers cannot be of two−digit or three−digit.Therefore, both will become a one−digit number.Thus, there is no solution possible.
The document RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
FAQs on RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the concept of "Playing with Numbers" in Class 8 Mathematics? |  |
Ans. "Playing with Numbers" is a chapter in Class 8 Mathematics that focuses on various number patterns, divisibility rules, and number operations. Students learn how to identify prime and composite numbers, find factors and multiples, and solve problems involving number operations.
| 2. How can I determine if a number is prime or composite? | |
Ans. To determine if a number is prime or composite, we need to check if it has any factors other than 1 and itself. If a number has factors other than these, it is composite. If it only has 1 and itself as factors, it is prime. For example, to check if 23 is prime or composite, we need to see if it has any factors other than 1 and 23. Since it doesn't, 23 is a prime number.
| 3. What are factors and multiples? How are they related? | |
Ans. Factors are the numbers that divide a given number completely without leaving any remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the numbers that are obtained by multiplying a given number by any whole number. For example, the multiples of 5 are 5, 10, 15, 20, and so on. Factors and multiples are related in the sense that the factors of a number are also its multiples. For example, the factors of 6 (1, 2, 3, and 6) are also its multiples.
| 4. How can I find the LCM and HCF of two or more numbers? | |
Ans. To find the Least Common Multiple (LCM) of two or more numbers, we need to find the smallest number that is divisible by all the given numbers. One way to find the LCM is by listing the multiples of each number and finding the smallest common multiple. To find the Highest Common Factor (HCF) of two or more numbers, we need to find the largest number that divides all the given numbers. One way to find the HCF is by listing the factors of each number and finding the largest common factor.
| 5. How can I apply divisibility rules to quickly check if a number is divisible by another number? | |
Ans. Divisibility rules are rules that help us determine if a number is divisible by another number without performing the actual division. For example, a number is divisible by 2 if its last digit is even, and it is divisible by 3 if the sum of its digits is divisible by 3. Similarly, there are rules for divisibility by 4, 5, 6, 9, and 10. By applying these rules, we can quickly check if a number is divisible by another number, which can be useful in simplifying calculations and solving problems.
Related Exams
About this Document
|
4.94/5 Rating |
|
Nov 22, 2024 Last updated |
Document Description: RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) for Class 8 2024 is part of RD Sharma Solutions for Class 8 Mathematics preparation.
The notes and questions for RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) have been prepared according to the Class 8 exam syllabus. Information about RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) covers topics
like and RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1).
Introduction of RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) in English is available as part of our RD Sharma Solutions for Class 8 Mathematics
for Class 8 & RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) in Hindi for RD Sharma Solutions for Class 8 Mathematics course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics
Description
Full syllabus notes, lecture & questions for RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics - Class 8 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 8 Mathematics | Best notes, free PDF download
Information about RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1)
In this doc you can find the meaning of RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) defined & explained in the simplest way possible. Besides explaining types of
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics
,MCQs
,Summary
,Sample Paper
,study material
,Viva Questions
,Objective type Questions
,Free
,mock tests for examination
,Exam
,Important questions
,ppt
,RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics
,video lectures
,practice quizzes
,Semester Notes
,Previous Year Questions with Solutions
,past year papers
,RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) | RD Sharma Solutions for Class 8 Mathematics
,Extra Questions
,shortcuts and tricks
;
Additional Information about RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) for Class 8 Preparation
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Free PDF Download
The RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) now and kickstart your journey towards success in the Class 8 exam.
Importance of RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1)
The importance of RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Notes
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Notes on EduRev are your ultimate resource for success.
RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Class 8 Questions
The "RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) on the App
Students of Class 8 can study RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of RD Sharma Solutions for Class 8 Math Chapter 5 - Playing with Numbers (Part-1) is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup