RMS Voltage | Electrical Engineering SSC JE (Technical) - Electrical Engineering (EE) PDF Download

The RMS or effective value of a sinusoidal waveform gives the same heating effect of an equivalent DC supply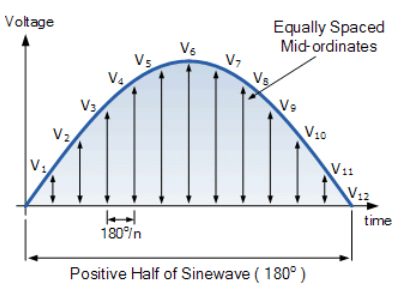

• In our tutorial about the AC Waveform we looked briefly at the RMS Voltage value of a sinusoidal waveform and said that this RMS value gives the same heating effect as an equivalent DC power and in this tutorial we will expand on this theory a little more by looking at RMS voltages and currents in more detail.
• The term “RMS” stands for “Root-Mean-Squared”. Most books define this as the “amount of AC power that produces the same heating effect as an equivalent DC power”, or something similar along these lines, but an RMS value is more than just that.
• The RMS value is the square root of the mean (average) value of the squared function of the instantaneous values. The symbols used for defining an RMS value are V_RMS or I_RMS.
• The term RMS, ONLY refers to time-varying sinusoidal voltages, currents or complex waveforms were the magnitude of the waveform changes over time and is not used in DC circuit analysis or calculations were the magnitude is always constant.
• When used to compare the equivalent RMS voltage value of an alternating sinusoidal waveform that supplies the same electrical power to a given load as an equivalent DC circuit, the RMS value is called the “effective value” and is generally presented as: V_eff or I_eff.
• In other words, the effective value is an equivalent DC value which tells you how many volts or amps of DC that a time-varying sinusoidal waveform is equal to in terms of its ability to produce the same power.
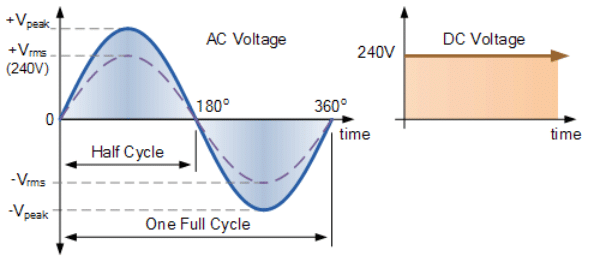
• For example, the domestic mains supply in the United Kingdom is 240Vac. This value is assumed to indicate an effective value of “240 Volts rms”. This means then that the sinusoidal rms voltage from the wall sockets of a UK home is capable of producing the same average positive power as 240 volts of steady DC voltage as shown below.

RMS Voltage Equivalent

So how do we calculated the RMS Voltage of a sinusoidal waveform. The RMS voltage of a sinusoid or complex waveform can be determined by two basic methods.

• Graphical Method: which can be used to find the RMS value of any non-sinusoidal time-varying waveform by drawing a number of mid-ordinates onto the waveform.
• Analytical Method: is a mathematical procedure for finding the effective or RMS value of any periodic voltage or current using calculus.

RMS Voltage Graphical Method

• Whilst the method of calculation is the same for both halves of an AC waveform, for this example we will consider only the positive half cycle. The effective or rms value of a waveform can be found with a reasonable amount of accuracy by taking equally spaced instantaneous values along the waveform.
• The positive half of the waveform is divided up into any number of “n” equal portions or mid-ordinates and the more mid-ordinates that are drawn along the waveform, the more accurate will be the final result.
• The width of each mid-ordinate will therefore be no degrees and the height of each mid-ordinate will be equal to the instantaneous value of the waveform at that time along the x-axis of the waveform.

Graphical Method

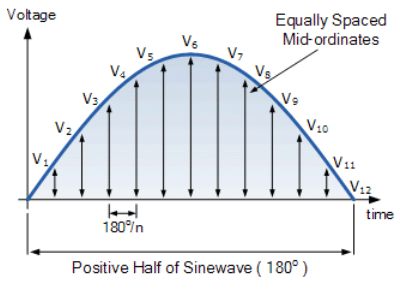
• Each mid-ordinate value of a waveform (the voltage waveform in this case) is multiplied by itself (squared) and added to the next. This method gives us the “square” or Squared part of the RMS voltage expression.
• Next this squared value is divided by the number of mid-ordinates used to give us the Mean part of the RMS voltage expression, and in our simple example above the number of mid-ordinates used was twelve (12). Finally, the square root of the previous result is found to give us the Root part of the RMS voltage.
• Then we can define the term used to describe an rms voltage (V_RMS) as being “the square root of the mean of the square of the mid-ordinates of the voltage waveform” and this is given as:
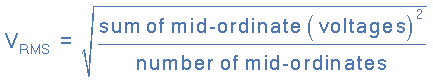  and for our simple example above, the RMS voltage will be calculated as: 
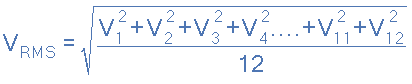  So lets assume that an alternating voltage has a peak voltage (Vpk) of 20 volts and by taking 10 mid-ordinate values is found to vary over one half cycle as follows:

The RMS voltage is therefore calculated as: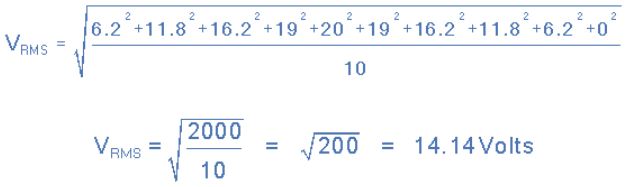
Then the RMS Voltage value using the graphical method is given as: 14.14 Volts.

RMS Voltage Analytical Method

• The graphical method above is a very good way of finding the effective or RMS voltage, (or current) of an alternating waveform that is not symmetrical or sinusoidal in nature. In other words the waveform shape resembles that of a complex waveform.
• However, when dealing with pure sinusoidal waveforms we can make life a little bit easier for ourselves by using an analytical or mathematical way of finding the RMS value.
• A periodic sinusoidal voltage is constant and can be defined as V_(t) = V_max*cos(ωt) with a period of T. Then we can calculate the root-mean-square (rms) value of a sinusoidal voltage (V_(t)) as:
  
• Integrating through with limits taken from 0 to 360^o or “T”, the period gives:
  
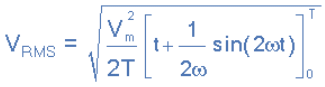
• Where: Vm is the peak or maximum value of the waveform. Dividing through further as ω = 2π/T, the complex equation above eventually reduces down too:

RMS Voltage Equation

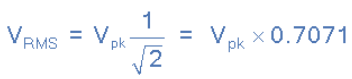
Then the RMS voltage (V_RMS) of a sinusoidal waveform is determined by multiplying the peak voltage value by 0.7071, which is the same as one divided by the square root of two ( 1/√2 ). The RMS voltage, which can also be referred to as the effective value, depends on the magnitude of the waveform and is not a function of either the waveforms frequency nor its phase angle.

From the graphical example above, the peak voltage (V_pk) of the waveform was given as 20 Volts. By using the analytical method just defined we can calculate the RMS voltage as being:
V_RMS = V_pk * 0.7071 = 20 x 0.7071 = 14.14V

Note that this value of 14.14 volts is the same value as for the previous graphical method. Then we can use either the graphical method of mid-ordinates, or the analytical method of calculation to find the RMS voltage or current values of a sinusoidal waveform.

Note that multiplying the peak or maximum value by the constant 0.7071, ONLY applies to sinusoidal waveforms. For non-sinusoidal waveforms the graphical method must be used.

But as well as using the peak or maximum value of the sinusoid, we can also use the peak-to-peak (V_P-P) value or the average (V_AVG) value to find the sinusoids equivalent root mean squared value as shown:

Sinusoidal RMS Values

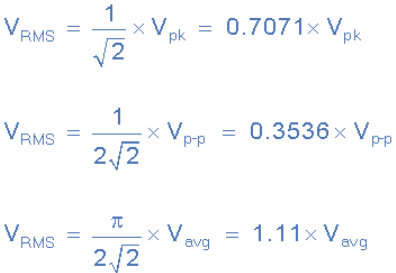
RMS Voltage Summary

• Then to summarize. When dealing with alternating voltages (or currents) we are faced with the problem of how do we represent a voltage or signal magnitude. One easy way is to use the peak values for the waveform. Another common method is to use the effective value which is also known by its more common expression of Root Mean Square or simply the RMS value.
• The root mean squared, RMS value of a sinusoid is not the same as the average of all the instantaneous values. The ratio of the RMS value of voltage to the maximum value of voltage is the same as the ratio of the RMS value of current to the maximum value of current.
• Most multi-meters, either voltmeters or ammeters, measure RMS value assuming a pure sinusoidal waveform. For finding the RMS value of non-sinusoidal waveform a “True RMS Multimeter” is required.
• The RMS value of a sinusoidal waveform gives the same heating effect as a DC current of the same value. That is if a direct current, I passes through a resistance of R ohms, the DC power consumed by the resistor as heat will therefore be I²R watts.
• Then if an alternating current, i = I_max*sinθ flows through the same resistance, the AC power converted into heat will be: I²_rms*R watts.
• Then when dealing with alternating voltages and currents, they should be treated as RMS values unless otherwise stated. Therefore an alternating current of 10 amperes will have the same heating effect as a direct current of 10 amperes and a maximum value of 14.14 amperes.
• Having now determined the RMS value of an alternating voltage (or current) waveform, in the next tutorial we will look at calculating the Average value, V_AVG of an alternating voltage and finally compare the two.