RS Aggarwal Solutions: Factorisation of Polynomials- 2 | Mathematics (Maths) Class 9 PDF Download
RS Aggarwal Solutions: Exercise 3B - Factorisation of Polynomials
Q.1. Factorise: 9x2 – 16y2
Ans. 9x2−16y2
=(3x)2−(4y)2
=(3x+4y)(3x−3y)
[a2−b2=(a+b)(a−b)]
Q.2. Factorise: (25/4 x2−1/9 y2)
Ans. (25/4 x2−1/9 y2)
=(5/2 x)2−(1/3 y)2
=(5/2 x + 1/3 y)(5/2 x−1/3 y)
[a2−b2=(a+b)(a−b)]
Q.3. Factorise: 81 – 16x2
Ans. 81−16x2
=92−(4x)2
=(9+4x)(9−4x) [a2−b2=(a+b)(a−b)]
Q.4. Factorise: 5 – 20x2
Ans. 5−20x2
=5(1−4x2)
=5[12−(2x)2]
=5(1+2x)(1−2x) [a2−b2=(a+b)(a−b)]
Q.5. Factorise: 2x4 – 32
Ans. 2x4−32
=2(x4−16)
=2[(x2)2−42]
=2(x2+4)(x2−4) [a2−b2=(a+b)(a−b)]
=2(x2+4)(x2−22)
=2(x2+4)(x+2)(x−2) [a2−b2=(a+b)(a−b)]
Q.6. Factorize: 3a3b − 243ab3
Ans. 3a3b−243ab3=3ab(a2−81b2)
=3ab[a2−(9b)2]
=3ab(a−9b)(a+9b)
Q.7. Factorize: 3x3 − 48x
Ans. 3x3−48x=3x(x2−16)
=3x(x2−42)
=3x(x−4) (x+4)
Q.8. Factorize: 27a2 − 48b2
Ans. 27a2−48b2=3(9a2−16b2)
=3[(3a)2−(4b)2]
=3(3a−4b)(3a+4b)
Q.9. Factorize: x − 64x3
Ans. x−64x3=x(1−64x2)
=x[1−(8x)2]
=x(1−8x) (1+8x)
Q.10. Factorize: 8ab2 − 18a3
Ans. 8ab2−18a3=2a(4b2−9a2)
=2a[(2b)2−(3a)2]
=2a(2b−3a)(2b+3a)
Q.11. Factorize: 150 − 6x2
Ans. 150−6x2=6(25−x2)
=6(52−x2)
=6(5−x)(5+x)
Q.12. Factorise: 2 – 50x2
Ans. 2−50x2
=2(1−25x2)
=2[12−(5x)2]
=2(1+5x)(1−5x) [a2−b2=(a+b)(a−b)]
Q.13. Factorise: 20x2 – 45
Ans. 20x2−45
=5(4x2−9)
=5[(2x)2−32]
=5(2x+3)(2x−3) [a2−b2=(a+b)(a−b)]
Q.14. Factorise: (3a + 5b)2 – 4c2
Ans. (3a+5b)2−4c2
=(3a+5b)2−(2c)2
=(3a+5b+2c)(3a+5b−2c) [a2−b2=(a+b)(a−b)]
Q.15. Factorise: a2 – b2 – a – b
Ans. a2−b2−a−b
=(a+b)(a−b)−1(a+b) [a2−b2=(a+b)(a−b)]
=(a+b)[(a−b)−1]
=(a+b)(a−b−1)
Q.16. Factorise: 4a2 – 9b2 – 2a – 3b
Ans. 4a2−9b2−2a−3b
=(2a)2−(3b)2−1(2a+3b)
=(2a+3b)(2a−3b)−1(2a+3b) [a2−b2=(a+b)(a−b)]
=(2a+3b)[(2a−3b)−1]
=(2a+3b)(2a−3b−1)
Q.17. Factorise: a2 – b2 + 2bc – c2
Ans. a2−b2+2bc−c2
=a2−(b2−2bc+c2)
=a2−(b−c)2 [a2−2ab+b2=(a−b)2]
=[a+(b−c)][a−(b−c)] [a2−b2=(a+b)(a−b)]
=(a+b−c)(a−b+c)
Q.18. Factorise: 4a2 – 4b2 + 4a + 1
Ans. 4a2−4b2+4a+1
=(4a2+4a+1)−4b2
=[(2a)2+2×2a×1+12]−4b2
=(2a+1)2−(2b)2 [a2+2ab+b2=(a+b)2]
=[(2a+1)+2b] [(2a+1)−2b] [a2−b2=(a+b)(a−b)]
=(2a+1+2b)(2a+1−2b)
=(2a+2b+1)(2a−2b+1)
Q.19. Factorize: a2 + 2ab + b2 − 9c2
Ans. a2+2ab+b2−9c2=(a+b)2−(3c)2
=(a+b−3c)(a+b+3c)
Q.20. Factorize: 108a2 − 3(b − c)2
Ans. 108a2−3(b−c)2=3[36a2−(b−c)2]
=3[(6a)2−(b−c)2]
=3(6a−b+c)(6a+b−c)
Q.21. Factorize: (a + b)3 − a − b
Ans. (a+b)3−a−b=(a+b)3−(a+b)
=(a+b)[(a+b)2−1]
=(a+b)[(a+b)2−12]
=(a+b)(a+b−1)(a+b+1)
Q.22. Factorise: x2 + y2 – z2 – 2xy
Ans. x2+y2−z2−2xy
=(x2+y2−2xy)−z2
=(x−y)2−z2 [a2−2ab+b2=(a−b)2]
=(x−y+z)(x−y−z) [a2−b2=(a+b)(a−b)]
Q.23. Factorise: x2 + 2xy + y2 – a2 + 2ab – b2
Ans. x2+2xy+y2−a2+2ab−b2
=(x2+2xy+y2)−(a2−2ab+b2)
=(x+y)2−(a−b)2 [a2+2ab+b2=(a+b)2 and a2−2ab+b2=(a−b)2]
=[(x+y)+(a−b)][(x+y)−(a−b)] [a2−b2=(a+b)(a−b)]
=(x+y+a−b)(x+y−a+b)
Q.24. Factorise: 25x2 – 10x + 1 – 36y2
Ans. 25x2−10x +1−36y2
=[(5x)2−2×5x×1+12]−(6y)2
=(5x−1)2−(6y)2 [a2−2ab+b2=(a−b)2]
=[(5x−1+6y)][(5x−1−6y)] [a2−b2=(a+b)(a−b)]
=(5x+6y−1)(5x−6y−1)
Q.25. Factorize: a − b − a2 + b2
Ans. a−b−a2+b2=(a−b)−(a2−b2)
=(a−b)−(a−b)(a+b)
=(a−b)[1−(a+b)]
=(a−b)(1−a−b)
Q.26. Factorize: a2 − b2 − 4ac + 4c2
Ans. a2−b2−4ac+4c2
=(a2−4ac+4c2)−b2
=a2−2×2a×c +(2c)2−b2
=(a−2c)2−b2
=(a−2c+b)(a−2c−b)
Q.27. Factorize: 9 − a2 + 2ab − b2
Ans. 9−a2+2ab−b2=9−(a2−2ab+b2)
=32−(a−b)2
=[3−(a−b)][3+(a−b)]
=(3−a+b)(3+a−b)
Q.28. Factorize: x3 − 5x2 − x + 5
Ans. x3−5x2−x+5
=x2(x−5)−1(x−5)
=(x−5)(x2−1)
=(x−5)(x2−12)
=(x−5)(x−1)(x+1)
Q.29. Factorise: 1 + 2ab – (a2 + b2)
Ans. 1+2ab−(a2+b2)
=1+2ab−a2−b2
=1−a2+2ab−b2
=12−(a2−2ab+b2)
=12−(a−b)2 [a2−2ab+b2=(a−b)2]
=[1+(a−b)][1−(a−b)] [a2−b2=(a+b)(a−b)]
=(1+a−b)(1−a+b)
Q.30. Factorise: 9a2 + 6a + 1 – 36b2
Ans. 9a2+6a+1−36b2
=[(3a)2+2×3a×1+12]−(6b)2
=(3a+1)2−(6b)2 [a2+2ab+b2=(a+b)2]
=(3a+1−6b)(3a+1+6b) [a2−b2=(a−b)(a+b)]
=(3a−6b+1)(3a+6b+1)
Q.31. Factorize: x2 − y2 + 6y − 9
Ans. x2−y2+6y−9
=x2−(y2−6y+9)
=x2−(y2−2×y×3 +32)
=x2−(y−3)2
=[x+(y−3)][x−(y−3)]
=(x+y−3)(x−y+3)
Q.32. Factorize: 4x2 − 9y2 − 2x − 3y
Ans. 4x2−9y2−2x−3y
=(4x2−9y2)−(2x+3y)
=[(2x)2−(3y)2]−(2x+3y)
=(2x−3y)(2x+3y)−1(2x+3y)
=(2x+3y)(2x−3y−1)
Q.33. Factorize: 9a2 + 3a − 8b − 64b2
Ans. 9a2+3a−8b−64b2
=9a2−64b2+3a−8b
=(3a)2−(8b)2+(3a−8b)
=(3a−8b)(3a+8b)+1(3a−8b)
=(3a−8b)(3a+8b+1)
Q.34. Factorise: x2+1/x2−3
Ans. x2+1/x2−3
=x2+1/x2−2−1
=[x2+(1/x)2−2×x×1/x]−1
=(x−1/x)2−12 [a2−2ab+b2=(a−b)2]
=(x−1/x+1)(x−1/x−1) [a2−b2=(a−b)(a+b)]
Q.35. Factorise: x2−2+1/x2 y2
Ans. x2−2+1/x2−y2
=[x2−2×x×1/x+(1/x)2]−y2
=(x−1/x)2−y2 [a2−2ab+b2=(a−b)2]
=(x−1/x+y)(x−1/x−y) [a2−b2=(a−b)(a+b)]
Disclaimer: The expression of the question should be x2−2+1/x2−y2. The same has been done before solving the question.
Q.36. Factorise: x4+4/x4
Ans. x4+4/x4
=x4+4/x4+4−4
=[(x2)2+(2/x2)2+2×(x2)×(2/x2)]−22
=(x2+2/x2)2−22 [a2+2ab+b2=(a+b)2]
=(x2+2/x2+2)(x2+2/x2−2) [a2−b2=(a+b)(a−b)]
Q.37. Factorise: x8 – 1
Ans. x8−1=(x4)2−12
=(x4+1)(x4−1) [a2−b2=(a+b)(a−b)]
=(x4+1)[(x2)2−12]
=(x4+1)(x2+1)(x2−1) [a2−b2=(a+b)(a−b)]
=(x4+1)(x2+1)(x2−1)2
=(x4+1)(x2+1)(x+1)(x−1) [a2−b2=(a+b)(a−b)]
Q.38. Factorise: 16x4 – 1
Ans. 16x4−1
=(4x2)2−12
=(4x2+1)(4x2−1) [a2−b2=(a+b)(a−b)]
=(4x2+1)[(2x)2−12]
=(4x2+1)(2x+1)(2x−1) [a2−b2=(a+b)(a−b)]
Q.39. 81x4 – y4
Ans. 81x4−y4
=(9x2)2−(y2)2
=(9x2+y2)(9x2−y2) [a2−b2=(a+b)(a−b)]
=(9x2+y2)[(3x)2−y2]
=(9x2+y2)(3x+y)(3x−y) [a2−b2=(a+b)(a−b)]
Q.40. x4 – 625
Ans. x4−625
=(x2)2−252
=(x2+25)(x2−25) [a2−b2=(a+b)(a−b)]
RS Aggarwal Solutions: Exercise 3C - Factorisation of Polynomials
Q.1. Factorize: x2 + 11x + 30
Ans. We have:
x2+11x+30
We have to split 11 into two numbers such that their sum of is 11 and their product is 30.
Clearly, 5+6=11 and 5×6=30.
∴ x2+11x+30
= x2+5x+6x+30
= x(x+5)+6(x+5)
=(x+5)(x+6)
Q.2. Factorize: x2 + 18x + 32
Ans. We have:
x2+18x+32
We have to split 18 into two numbers such that their sum is 18 and their product is 32.
Clearly, 16+2=18 and 16×2=32.
∴x2+18x+32
=x2+16x+2x+32
=x(x+16)+2(x+16)
=(x+16)(x+2)
Q.3. Factorise: x2 + 20x – 69
Ans. x2+20x-69
=x2+23x-3x-69
=x(x+23)-3(x+23)
=(x+23)(x-3)
Q.4. x2 + 19x – 150
Ans. x2+19x-150
=x2+25x-6x-150
=x(x+25)-6(x+25)
=(x+25)(x-6)
Q.5. Factorise: x2 + 7x – 98
Ans. x2+7x-98
=x2+14x-7x-98
=x(x+14)-7(x+14)
=(x+14)(x-7)
Q.6. Factorise: x2+2√3x–24
Ans. x2+2√3x–24
= x2+4√3x-2√3x-24
= x(x+4√3)-2√3(x+4√3)
=(x+4√3)(x-2√3)
Q.7. Factorise: x2 – 21x + 90
Ans. x2-21x+90
=x2-15x-6x+90
=x(x-15)-6(x-15)
=(x-6)(x-15)
Q.8. Factorise: x2 – 22x + 120
Ans. x2-22x+120
=x2-12x-10x+120
=x(x-12)-10(x-12)
=(x-10)(x-12)
Q.9. Factorise: x2 – 4x + 3
Ans. x2-4x+3
=x2-3x-x+3
=x(x-3)-1(x-3)
=(x-1)(x-3)
Q.10. Factorise: x2+7√6x+60
Ans. x2+7√6x+60
=x2+5√6x+2√6x+60
=x(x+5√6)+2√6(x+5√6)=(x+5√6)(x+2√6)
Q.11. Factorise: x2+3√3x+6
Ans. x2+3√3x+6
=x2+2√3x+√3x+6
=x(x+2√3)+√3(x+2√3)
=(x+2√3)(x+√3)
Q.12. Factorise: x2+6√6x+48
Ans. x2+6√6x+48
=x2+4√6x+2√6x+48
=x(x+4√6)+2√6(x+4√6)
=(x+4√6)(x+2√6)
Q.13. Factorise: x2+5√5x+30
Ans. x2+5√5x+30
=x2+3√5x+2√5x+30
=x(x+3√5)+2√5(x+3√5)=(x+3√5)(x+2√5)
Q.14. Factorise: x2-24x-180
Ans. x2-24x-180
=x2-30x+6x-180
=x(x-30)+6(x-30)
=(x-30)(x+6)
Q.15. Factorise: x2 – 32x – 105
Ans. x2-32x-105
=x2-35x+3x-105
=x(x-35)+3(x-35)
=(x-35)(x+3)
Q.16. Factorise: x2 – 11x – 80
Ans. x2-11x-80
=x2-16x+5x-80
=x(x-16)+5(x-16)
=(x-16)(x+5)
Q.17. Factorise: 6 – x – x2
Ans. -x2-x+6
=-x2-3x+2x+6
=-x(x+3)+2(x+3)
=(x+3)(-x+2)
=(x+3)(2-x)
Q.18. Factorise: x2-√3x-6
Ans. x2-√3x-6
=x2-2√3x+√3x-6
=x(x-2√3)+√3(x-2√3)
=(x-2√3)(x+√3)
Q.19. Factorise: 40 + 3x – x2
Ans. -x2+3x+40
=-x2+8x-5x+40
=-x(x-8)-5(x-8)
=(x-8)(-x-5)
=(8-x)(x+5)
Q.20. Factorise: x2 – 26x + 133
Ans. x2-26x+133
=x2-19x-7x+133
=x(x-19)-7(x-19)
=(x-19)(x-7)
Q.21. Factorise: x2-2√3x-24
Ans. x2-2√3x-24
=x2-4√3x+2√3x-24
=x(x-4√3)+2√3(x-4√3)
=(x-4√3)(x+2√3)
Q.22. Factorise: x2-3√5x-20
Ans. x2-3√5x-20
=x2-4√5x+√5x-20
=x(x-4√5)+√5(x-4√5)
=(x-4√5)(x+√5)
Q.23. Factorise: x2+√2x-24
Ans. x2+√2x-24
=x2+4√2x-√2x-24
=x(x+4√2)-3√2(x+4√2)
=(x+4√2)(x-3√2)
Q.24. Factorise: x2-2√2x-30
Ans. x2-2√2x-30
=x2-5√2x+3√2x-30
=x(x-5√2)+3√2(x-5√2)
=(x-5√2)(x+3√2)
Q.25. Factorize: x2 − x − 156
Ans. We have: x2-x-156
We have to split (-1) into two numbers such that their sum is (-1) and their product is (-156).
Clearly, -13+12=-1 and -13×12=-156.
∴x2-x-156
=x2-13x+12x-156
=x(x-13)+12(x-13)
=(x-13)(x+12)
Q.26. Factorise: x2 – 32x – 105
Ans. x2-32x-105
=x2-35x+3x-105
=x(x-35)+3(x-35)
=(x-35)(x+3)
Q.27. Factorise: 9x2 + 18x + 8
Ans. 9x2+18x+8
=9x2+12x+6x+8
=3x(3x+4)+2(3x+4)
=(3x+4)(3x+2)
Q.28. Factorise: 6x2 + 17x + 12
Ans. 6x2+17x+12
=6x2+9x+8x+12
=3x(2x+3)+4(2x+3)
=(2x+3)(3x+4)
Q.29. Factorize: 18x2 + 3x − 10
Ans. We have: 18x2+3x-10
We have to split 3 into two numbers such that their sum is 3 and their product is (-180), i.e., 18×(-10).
Clearly, 15+(-12)=3 and 15×(-12)=-180.
∴18x2+3x-10
=18x2+15x-12x-10
=3x(6x+5)-2(6x+5)
=(6x+5)(3x-2)
Q.30. Factorize: 2x2 + 11x − 21
Ans. We have: 2x2+11x-21
We have to split 11 into two numbers such that their sum is 11 and their product is (-42),
i.e., 2×(-21).
Clearly, 14+(-3)
=11 and 14×(-3)
=-42.
∴2x2+11x-21
=2x2+14x-3x-21
=2x(x+7)-3(x+7)
=(x+7)(2x-3)
Q.31. Factorize: 15x2 + 2x − 8
Ans. We have: 15x2+2x-8
We have to split 2 into two numbers such that their sum is 2 and their product is (-120), i.e., 15×(-8).
Clearly, 12+(-10)=2
and 12×(-10)=-120.
∴15x2+2x-8
=15x2+12x-10x-8
=3x(5x+4)-2(5x+4)
=(5x+4)(3x-2)
Q.32. Factorise: 21x2 + 5x – 6
Ans. 21x2+5x-6
=21x2+14x-9x-6
=7x(3x+2)-3(3x+2)
=(3x+2)(7x-3)
Q.33. Factorize: 24x2 − 41x + 12
Ans. We have: 24x2-41x+12
We have to split (-41) into two numbers such that their sum is (-41) and their product is 288, i.e., 24×12.
Clearly, (-32)+(-9)=-41 and (-32)×(-9)=288.
∴24x2-41x+12
=24x2-32x-9x+12
=8x(3x-4)-3(3x-4)
=(3x-4)(8x-3)
Q.34. Factorise: 3x2 – 14x + 8
Ans. 3x2-14x+8
=3x2-12x-2x+8
=3x(x-4)-2(x-4)
=(x-4)(3x-2)
Hence, factorisation of 3x2 – 14x + 8 is (x-4)(3x-2).
Q.35. Factorize: 2x2 + 3x − 90
Ans. We have: 2x2+3x-90
We have to split 3 into two numbers such that their sum is 3 and their product is (-180), i.e., 2×(-90).
Clearly, -12 + 15 = 3 and -12×15 = -180.
∴2x2+3x-90
=2x2-12x+15x-90
=2x(x-6)+15(x-6)
=(x-6)(2x+15)
Q.36. Factorize: √5x2+2x-3√5
Ans. We have:√5x2+2x-3√5
We have to split 2 into two numbers such that their sum is 2 and product is (-15), i.e.,√5×(-3√5).
Clearly, 5+(-3)=2 and 5×(-3)=-15.
∴√5x2+2x-3√5
=√5x2+5x-3x-3√5
=√5x(x+√5)-3(x+√5)
=(x+√5)(√5x-3)
Q.37. Factorize: 2√3x2+x-5√3
Ans. We have: 2√3x2+x-5√3
We have to split 1 into two numbers such that their sum is 1 and product is 30, i.e.,2√3×(-5√3).
Clearly, 6+(-5)=1 and 6×(-5)=-30.
∴2√3x2+x-5√3
=2√3x2+6x-5x-5√3
=2√3x(x+√3)-5(x+√3)
=(x+√3)(2√3x-5)
Q.38. Factorize: 7x2+2√14x+2
Ans. We have: 7x2+2√14x+2
We have to split 2√14 into two numbers such that their sum is 2√14 and product is 14.
Clearly, √14+√14=2
√14 and √14×√14=14.
∴7x2+2√14x+2
=7x2+√14x+√14x+2
=√7x(√7x+√2)+√2(√7x+√2)
=(√7x+√2)(√7x+√2)
=(√7x+√2)2
Q.39. Factorize: 6√3x2-47x+5√3
Ans. We have: 6√3x2-47x+5√3
Now, we have to split (-47) into two numbers such that their sum is (-47) and their product is 90.
Clearly, (-45)+(-2)=-47 and (-45)×(-2)=90.
∴6√3x2-47x+5√3
=6√3x2-2x-45x+5√3
=2x(3√3x-1)-5√3(3√3x-1)
=(3√3x-1)(2x-5√3)
Q.40. Factorize: 5√5x2+20x+3√5
Ans. We have: 5√5x2+20x+3√5
We have to split 20 into two numbers such that their sum is 20 and their product is 75.
Clearly, 15+5=20 and 15×5=75
∴5√5x2+20x+3√5
=5√5x2+15x+5x+3√5
=5x(√5x+3)+√5(√5x+3)
=(√5x+3)(5x+√5)
Q.41. Factorise: √3x2+10x+8√3
Ans. √3x2+10x+8√3
=√3x2+6x+4x+8√3
=√3x(x+2√3)+4(x+2√3)
=(x+2√3)(√3x+4)
Hence, factorisation of √3x2+10x+8√3 is (x+2√3)(√3x+4).
Q.42. Factorize: √2x2+3x+√2
Ans. We have: √2x2+3x+√2
We have to split 3 into two numbers such that their sum is 3 and their product is 2, i.e.,
√2×√2.
Clearly, 2+1=3 and 2×1=2.
∴√2x2+3x+√2
=√2x2+2x+x+√2
=√2x(x+√2)+1(x+√2)
=(x+√2)(√2x+1)
Q.43. Factorize: 2x2+3√3x+3
Ans. We have: 2x2+3√3x+3
We have to split 3√3 into two numbers such that their sum is 3√3 and their product is 6, i.e.,2×3.
Clearly, 2√3+√3=3√3 and 2√3×√3=6.
∴2x2+3√3x+3=2x2+2√3x+√3x+3
=2x(x+√3)+√3(x+√3)
=(x+√3)(2x+√3)
Q.44. Factorize: 15x2 − x − 128
Ans. We have: 15x2-x-28
We have to split (-1) into two numbers such that their sum is (-1) and their product is (-420), i.e., 15×(-28).
Clearly, (-21)+20=-1 and (-21)×20=-420.
∴15x2-x-28
=15x2-21x+20x-28
=3x(5x-7)+4(5x-7)
=(5x-7)(3x+4)
Q.45. Factorize: 6x2 − 5x − 21
Ans. We have: 6x2-5x-21
We have to split (-5) into two numbers such that their sum is (-5) and their product is (-126), i.e., 6×(-21).
Clearly, 9+(-14)=-5 and 9×(-14)=-126.
∴6x2-5x-21
=6x2+9x-14x-21
=3x(2x+3)-7(2x+3)
=(2x+3)(3x-7)
Q.46. Factorize: 2x2 − 7x − 15
Ans. We have: 2x2-7x-15
We have to split (-7) into two numbers such that their sum is (-7) and their product is (-30), i.e., 2×(-15).
Clearly, (-10)+3=-7 and (-10)×3=-30.
∴2x2-7x-15
=2x2-10x+3x-15
=2x(x-5)+3(x-5)
=(x-5)(2x+3)
Q.47. Factorize: 5x2 − 16x − 21
Ans. We have: 5x2-16x-21
We have to split (-16) into two numbers such that their sum is (-16) and their product is (-105), i.e., 5×(-21).
Clearly, (-21)+5=-16 and (-21)×5=-105.
∴ 5x2-16x-21
=5x2+5x-21x-21
=5x(x+1)-21(x+1)
=(x+1)(5x-21)
Q.48. Factorise: 6x2 – 11x – 35
Ans. 6x2-11x-35
=6x2-21x+10x-35
=3x(2x-7)+5(2x-7)
=(2x-7)(3x+5)
Hence, factorisation of 6x2 – 11x – 35 is (2x-7)(3x+5).
Q.49. Factorise: 9x2 – 3x – 20
Ans. 9x2-3x-20
=9x2-15x+12x-20
=3x(3x-5)+4(3x-5)
=(3x-5)(3x+4)
Hence, factorisation of 9x2 – 3x – 20 is (3x-5)(3x+4).
Q.50. Factorize: 10x2 − 9x − 7
Ans. We have: 10x2-9x-7
We have to split (-9) into two numbers such that their sum is (-9) and their product is (-70), i.e., 10×(-7).
Clearly, (-14)+5=-9 and (-14)×5=-70.
∴10x2-9x-7
=10x2+5x-14x-7
=5x(2x+1)-7(2x+1)
=(2x+1)(5x-7)
Q.51. Factorize: x2-2x+7/16
Ans. We have:x2-2x+716
= (16x2-32x+7)/16
= 1/16 (16x2-32x+7)
Now, we have to split (-32) into two numbers such that their sum is (-32) and their product is 112, i.e., 16×7.
Clearly, (-4)+(-28)=-32 and (-4)×(-28)=112.
∴x2 - 2x + 7/16 = 1/16 (16x2-32x+7)
= 1/16 (16x2-4x-28x+7)
= 1/16 [4x(4x-1)-7(4x-1)]
= 1/16 (4x-1)(4x-7)
Q.52. Factorise: (1/3)x2-2x-9
Ans. (1/3)x2-2x-9 = (x2-6x-27)/3
= (x2-9x+3x-27)/3
= (x(x-9)+3(x-9))/3
= ((x-9)(x+3))/3
= (x-9)/3×(x+3)/1
=(1/3x-3)(x+3)
Hence, factorisation of (1/3) x2-2x-9 is (1/3x-3)(x+3).
Q.53. Factorise: x2+ 12/35 x+1/35
Ans. x2+ 12/35x+ 1/35
= (35x2+12x+1)/35
= (35x2+7x+5x+1)/35
= (7x(5x+1)+1(5x+1))/35= ((5x+1)(7x+1))/35
= (5x+1)/5 x (7x+1)/7
= (x+1/5) × (x+1/7)
Hence, factorisation of x2+12/35x+1/35is (x+1/5)(x+1/7).
Q.54. Factorise: 21x2-2x+ 1/21
Ans. 21x2-2x+1/21
=21x2-x-x+1/21
=21x(x-1/21)-1(x-1/21)
=(x-1/21)(21x-1)
Hence, factorisation of 21x2-2x+1/21 is (x-1/21)(21x-1).
Q.55. Factorise: 3/2 x2+16x+10
Ans. 3/2 x2+16x+10
Hence, factorisation of 3/2 x2+16x+10 is (x+10)(3/2x+1).
Q.56. Factorise: 2/3x2 - 17/3x-28
Ans. 2/3x2-17/3 x-28
Hence, factorisation of 2/3 x2- 17/3 x-28 is (1/3x-4)(2x+7).
Q.57. Factorise: 3/5 x2-19/5x+4
Ans. 3/5 x2-19/5 x+4
Hence, factorisation of 3/5 x2- 19/5 x+4 is (1/5 x-1)(3x-4).
Q.58. Factorise: 2x2-x+1/8
Ans. 2x2-x+1/8
Hence, factorisation of 2x2-x+1/8 is (x-1/4)(2x-1/2).
Q.59. Factorize: 2(x + y)2 − 9(x + y) − 5
Ans. We have: 2(x+y)2-9(x+y)-5
Let:(x+y)=u
Thus, the given expression becomes
2u2-9u-5
Now, we have to split (-9) into two numbers such that their sum is (-9) and their product is (-10).
Clearly, -10+1=-9 and -10×1=-10.
∴2u2-9u-5
=2u2-10u+u-5
=2u(u-5)+1(u-5)
=(u-5)(2u+1)
Putting u=(x+y), we get:
2(x+y)2 - 9(x+y) - 5
= (x+y-5)[2(x+y)+1]
= (x+y-5)(2x+2y+1)
Q.60. Factorize: 9(2a − b)2 − 4(2a − b) − 13
Ans. We have: 9(2a-b)2-4(2a-b)-13
Let:(2a-b)=p
Thus, the given expression becomes
9p2-4p-13
Now, we must split (-4) into two numbers such that their sum is (-4) and their product is (-117).
Clearly, -13+9=-4 and -13×9=-117.
∴ 9p2-4p-13
=9p2+9p-13p-13
=9p(p+1)-13(p+1)
=(p+1)(9p-13)
Putting p=(2a-b), we get: 9(2a-b)2-4(2a-b)-13
=[(2a-b)+1][9(2a-b)-13]
=(2a-b+1)[18a-9b-13]
Q. 61. Factorise: 7(x−2y)2−25(x−2y)+12
Ans. 7(x−2y)2−25(x−2y)+12
=7(x−2y)2−21(x−2y)−4(x−2y)+12
=[7(x−2y)](x−2y−3)−4(x−2y−3)
=[7(x−2y)−4](x−2y−3)
=(7x−14y−4)(x−2y−3)7x-2y2-25x-2y+12
=7x-2y2-21x-2y-4x-2y+12
=7x-2yx-2y-3-4x-2y-3
=7x-2y-4x-2y-3
=7x-14y-4x-2y-3
Hence, factorisation of 7(x−2y)2−25(x−2y)+12 is (7x−14y−4)(x−2y−3)
Q.62. Factorise: 10(3x+1/x)2−(3x+1/x)−3
Ans. 10(3x+1/x)2−(3x+1/x)−3
=10(3x+1/x)2−6(3x+1/x)+5(3x+1/x)−3
=[2(3x+1/x)][5(3x+1/x)−3]+1[5(3x+1/x)−3]
=[5(3x+1/x)−3][2(3x+1/x)+1]
=(15x+5/x−3)(6x+2/x+1)
Hence, factorisation of 10(3x+1/x)2−(3x+1/x)−3 is (15x+5/x−3)(6x+2/x+1)
Q.63. Factorise: 6(2x−3/x)2+7(2x−3/x)−20
Ans. 6(2x−3/x)2+7(2x−3/x)−20
=6(2x−3/x)2+15(2x−3x)−8(2x−3x)−20
=[3(2x−3/x)][2(2x−3/x)+5]−4[2(2x−3/x)+5]
=[2(2x−3/x)+5][3(2x−3/x)−4]
=(4x−6/x+5)(6x−9/x−4)
Hence, factorisation of 6(2x−3/x)2+7(2x−3/x)−20 is (4x−6/x+5)(6x−9/x−4)
Q.64. Factorise: (a+2b)2+101(a+2b)+100
Ans. (a+2b)2+101(a+2b)+100
=(a+2b)2+100(a+2b)+1(a+2b)+100
=(a+2b)[(a+2b)+100]+1[(a+2b)+100]
=[(a+2b)+1][(a+2b)+100]
=(a+2b+1)(a+2b+100)
Hence, factorisation of (a+2b)2+101(a+2b)+100 is (a+2b+1)(a+2b+100)
Q.65. Factorise: 4x4 + 7x2 – 2
Ans. 4x4+7x2−2
=4x4+8x2−x2−2
=4x2(x2+2)−1(x2+2)
=(4x2−1)(x2+2)
Hence, factorisation of 4x4 + 7x2 – 2 is (4x2−1)(x2+2)
Q.66. Evaluate {(999)2 – 1}.
Ans. {(999)2−1}
={(999)2−12}
=(999−1)(999+1)
=(998)(1000)
=998000
Hence, {(999)2 – 1} = 998000.
RS Aggarwal Solutions: Exercise 3D - Factorisation of Polynomials
Q.1. Expand:
(i) (a + 2b + 5c)2
(ii) (2b − b + c)2
(iii) (a − 2b − 3c)2
Ans. (i) (a+2b+5c)2
=(a)2 + (2b)2 +(5c)2+2(a)(2b)+2(2b)(5c)+2(5c)(a) =a2+4b2+25c2+4ab+20bc+10ac
(ii) (2a−b+c)2=[(2a)+(−b)+(c)]2
=(2a)2+(−b)2+(c)2+2(2a)(−b)+2(−b)(c)+4(a)(c)
=4a2+b2+c2−4ab−2bc+4ac
(iii) (a−2b−3c)2=[a+(−2b)+(−3c)]2
=(a)2+(−2b)2+(−3c)2+2(a)(−2b)+2(−2b)(−3c)+2(a)(−3c)
=a2+4b2+9c2−4ab+12bc−6ac
Q.2. Expand:
(i) (2a − 5b − 7c)2
(ii) (−3a + 4b − 5c)2
(iii) (12a−14a+2)2
Ans. (i) (2a−5b−7c)2
=[(2a)+(−5b)+(−7c)]2
=(2a)2+(−5b)2+(−7c)2+2(2a)(−5b)+2(−5b)(−7c)+2(2a)(−7c)
=4a2+25b2+49c2−20ab+70bc−28ac
(ii) (−3a+4b−5c)2=[(−3a)+(4b)+(−5c)]2
=(−3a)2+(4b)2+(−5c)2+2(−3a)(4b)+2(4b)(−5c)+2(−3a)(−5c)
=9a2+16b2+25c2−24ab−40bc+30ac
(iii) (1/2a−1/4b+2)2=[(a/2)+(−b/4)+(2)]2
=(a2)2+(−b4)2+(2)2+2(a/2)(−b/4)+2(−b/4)(2)+2(a/2)(2)
=a2/4+b2/16+4−ab/4−b+2a
Q.3. Factorize: 4x2 + 9y2 + 16z2 + 12xy − 24yz − 16xz.
Ans. We have: 4x2+9y2+16z2+12xy−24yz−16xz
=(2x)2+(3y)2+(−4z)2+2(2x)(3y)+2(3y)(−4z)+2(−4z)(2x)
=[(2x)+(3y)+(−4z)]2
=(2x+3y−4z)2
Q. 4. Factorize: 9x2 + 16y2 + 4z2 − 24xy + 16yz − 12xz
Ans. We have: 9x2+16y2+4z2−24xy+16yz−12xz
=(−3x)2+(4y)2+(2z)2+2(−3x)(4y)+2(4y)(2z)+2(2z)(−3x)
=[(−3x)+(4y)+(2z)]2
=(−3x+4y+2z)2
Q.5. Factorize: 25x2 + 4y2 + 9z2 − 20xy − 12yz + 30xz.
Ans. We have: 25x2+4y2+9z2−20xy−12yz+30xz
=(5x)2+(−2y)2+(3z)2+2(5x)(−2y)+2(−2y)(3z)+2(3z)(5x)
=[(5x)+(−2y)+(3z)]2
=(5x−2y+3z)2
Q.6. 16x2 + 4y2 + 9z2 – 16xy – 12yz + 24xz
Ans. 16x2+4y2+9z2−16xy−12yz+24xz
=(4x)2+(−2y)2+(3z)2+2(4x)(−2y)+2(−2y)(3z)+2(3z)(4x)
=(4x−2y+3z)2 [using a2+b2+c2+2ab+2bc+2ca=(a+b+c)2]
Hence, 16x2 + 4y2 + 9z2 – 16xy – 12yz + 24xz = (4x−2y+3z)2
Q.7. Evaluate
(i) (99)2
(ii) (995)2
(iii) (107)2
Ans. (i) (99)2=(100−1)2
=[(100)+(−1)]2
= (100)2+2×(100)×(−1)+(−1)2
=10000−200+1
=9801
(ii) (995)2=(1000−5)2
=[(1000)+(−5)]2
=(1000)2+2×(1000)×(−5)+(−5)2
=1000000−10000+25
=990025
(iii) (107)2=(100+7)2
=(100)2+2×(100)×(7)+(7)2
=10000+1400+49
=11449
RS Aggarwal Solutions: Exercise 3E - Factorisation of Polynomials
Q.1. Expand
(i) (3x + 2)3
(ii) (3a+1/4b)3
(iii) (1+2/3 a)3
Ans. (i) (3x+2)3=(3x)3+3×(3x)2x2+3×3x×(2)2+(2)3
=27x3+54x2+36x+8
(ii) (3a+1/4b)3=(3a)3+(1/4b)3+3(3a)2(1/4b)+3(3a)(14b)2 =27a3+1/64b3+27a2/4b+9a/16b2
(iii) (1+2/3a)3=(2/3a)3+3×(2/3a)2×1+3a2/3a×(1)2+(1)3 =827a3+43a2+2a+1iii 1+23a3=23a3+3×23a2×1+3a23a×12+13 =8/27a3+43a2+2a+1
Q.2. Expand
(i) (5a – 3b)3
(ii) (3x−5/x)3
(iii) (4/5a−2)3
Ans. (i) (5a−3b)3=(5a)3−(3b)3−3(5a)2(3b)+3(5a)(3b)2 =125a3−27b3−225a2b+135ab2
(ii) (3x−5/x)3=(3x)3−(5/x)3−3(3x)2(5/x)+3(3x)(5/x)2
=27x3−125/x3−135x+225/x
(iii) (4/5a−2)3=(4/5a)3−(2)3−3(4/5a)2(2)+3(4/5a)(2)2
=64/125a3−8−96/25a2+48/5a
Q.3. Factorise 8a3+27b3+36a2b+54ab2
Ans. 8a3+27b3+36a2b+54ab2
=(2a)3+(3b)3+3(2a)2(3b)+3(2a)(3b)2
=(2a+3b)3
Hence, factorisation of 8a3+27b3+36a2b+54ab2
Q.4. Factorise 64a3−27b3−144a2b+108ab2
Ans. 64a3−27b3−144a2b+108ab2
=(4a)3−(3b)3−3(4a)2(3b)+3(4a)(3b)2
=(4a-3b)3
Hence, factorisation of 64a3−27b3−144a2b+108ab2
Q.5. Factorise 1+27/125 a3+9a/5+27a2/24
Ans. 1+27/125 a3+9a/5+27a2/25
=(1)3+(3/5a)3+3(1)2(3/5 a)+3(1)(3/5a)2
Hence, factorisation of 1+27/125 a3+9a/5+27a2/25 is (1+3/5a)3
Q.6. Factorise 125x3−27y3−225x2y+135xy2
Ans. 125x3−27y3−225x2y+135xy2
=(5x)3−(3y)3−3(5x)2(3y)+3(5x)(3y)2
=(5x-3y)3
Hence, factorisation of 125x3−27y3−225x2y+135xy2 is (5x−3y)3
Q.7. Factorise: a3x3−3a2bx2+3ab2x−b3
Ans. a3x3−3a2bx2+3ab2x−b3
=(ax)3−(b)3−3(ax)2(b)+3(ax)(b)2
= (ax-b)3
Hence, factorisation of a3x3−3a2bx2+3ab2x−b3 is (ax−b)3.
Q.8. Factorise: 64/125a3−96/25a2+48/5a−8
Ans. 64/125 a3−96/25 a2+48/5 a−8
=(4/5 a)3−(2)3−3(4/5 a)2(2)+3(4/5 a)(2)2
=(4/5 a-2)3
Hence, factorisation of 64/125 a3−96/25 a2+48/5 a is (4/5a−2)3 is (4/5a-2)3.
Q.9. Factorise a3 – 12a(a – 4) – 64
Ans. a3−12a(a−4)−64
=a3−12a2+48a−64
=(a)3−(4)3−3(a)2(4)+3(a)(4)2
= (a-4)3
Hence, factorisation of a3 – 12a(a – 4) – 64 is (a−4)3.
Q.10. Evaluate
(i) (103)3
(ii) (99)3
Ans. (i) (103)3=(100+3)3
=(100)3+(3)3+3(100)2(3)+3(100)(3)2
=1000000+27+90000+2700
=1092727
(ii) (99)3=(100−1)3
=(100)3−(1)3−3(100)2(1)+3(100)(1)2
=1000000−1−30000+300
=1000300−30001
=970299
RS Aggarwal Solutions: Exercise 3F - Factorisation of Polynomials
Q.1. Factorize: x3 + 27
Ans. x3+27=(x)3+(3)3
=(x+3)(x2−3x+32)
=(x+3)(x2−3x+9)
Q.2. Factorise: 27a3 + 64b3
Ans. We know that x3+y3
=(x+y)(x2+y2−xy)x3+y3
Given: 27a3 + 64b3
x = 3a, y = 4b
27a3 + 64b3=(3a+4b)(9a2+16b2−12ab)
Q.3. Factorize: 125a3+1/8
Ans. 125a3+1/8=(5a)3+(1/2)3
=(5a+1/2)[(5a)2−5a×1/2+(1/2)2]
=(5a+1/2)(25a2−5a/2+1/4)
Q.4. Factorize: 216x3+1/125
Ans. 216x3+1/125=(6x)3+(1/5)3
=(6x+1/5)[(6x)2−6x×1/5+(1/5)2]
=(6x+1/5)(36x2−6x/5+1/25)
Q.5. Factorize: 16x4 + 54x
Ans. 16x4+54x
=2x(8x3+27)
=2x[(2x)3+(3)3]
=2x(2x+3)[(2x)2−2x×3+32]
=2x(2x+3)(4x2−6x+9)
Q.6. Factorize: 7a3 + 56b3
Ans. 7a3+56b3=7(a3+8b3)
=7[(a)3+(2b)3]
=7(a+2b)[a2−a×2b+(2b)2]
=7(a+2b)(a2−2ab+4b2)
Q.7. Factorize: x5 + x2
Ans. x5+x2=x2(x3+1)
=x2(x3+13)
=x2(x+1)(x2−x×1+12)
=x2(x+1)(x2−x+1)
Q.8. Factorize: a3 + 0.008
Ans. a3+0.008=a3+(0.2)3
=(a+0.2)[a2−a×(0.2)+(0.2)2]
=(a+0.2)(a2−0.2a+0.04)
Q.9. Factorise: 1 – 27a3
Ans. 1−27a3=13−(3a)3
=(1−3a)[12+1×3x+(3a)2]
=(1−3a)(1+3a+9a2)
Q.10. Factorize: 64a3 − 343
Ans. 64a3−343=(4a)3−(7)3
=(4a−7)(16a2+4a×7+72)
=(4a−7)(16a2+28a+49)
Q.11. Factorize: x3 − 512
Ans. x3−512 =x3−83
=(x−8)(x2+8x+82)
=(x−8)(x2+8x+64)
Q.12. Factorize: a3 − 0.064
Ans. a3−0.064=(a)3−(0.4)3
=(a−0.4)[a2+a×(0.4)+(0.4)2]
=(a−0.4)(a2+0.4a+0.16)
Q.13. Factorize: 8x3−1/27y3
Ans. 8x3−127y3=(2x)3−(1/3y)3
=(2x−1/3y)[(2x)2+2x×1/3y+(1/3y)2]
=(2x−1/3y)(4x2+2x/3y+1/9y2)
Q.14. Factorise: x3/216−8y3
Ans. We know a3−b3=(a−b)(a2+b2+ab)
We have,
x3/216−8y3=(x/6)3−(2y)3
So, a=x/6,b=2y
x3/216−8y3=(x/6−2y)((x/6)2+x/6×2y+(2y)2)
=(x/6−2y)(x2/36+xy/3+4y2)
Q.15. Factorize: x − 8xy3
Ans. x−8xy3=x(1−8y3)
=x[13−(2y)3]
=x(1−2y)(12+1×2y+(2y)2)
=x(1−2y)(1+2y+4y2)
Q.16. Factorise: 32x4 – 500x
Ans. 32x4 – 500x=4x(8x3−125)=4x((2x)3−53)
we know
a3−b3=(a−b)(a2+b2+ab)
a=2x,b=5
32x4 – 500x=4x((2x)3−53)
=4x(2x−5)(4x2+25+10x)
Q.17. Factorize: 3a7b − 81a4b4
Ans. 3a7b−81a4b4=3a4b(a3−27b3)
=3a4b[a3−(3b)3]
=3a4b(a−3b)[a2+a×3b+(3b)2]
=3a4b(a−3b)(a2+3ab+9b2)
Q.18. Factorise: x4 y4 – xy
Ans. Using the identity
a3−b3=(a−b)(a2+b2+ab)
x4 y4–xy=xy(x3y3−1)
=xy(xy−1)(x2y2+1+xy)
Q.19. Factorise: 8x2 y3 – x5
Ans. 8x2y3–x5=x2(8y3−x3)
=x2(2y−x)(4y2+x2+2xy)
Q.20. Factorise:1029 – 3x3
Ans. 1029–3x3
=3(343−x3)
=3(73−x3)
=3(7−x)(49+x2+7x)
Q.21. Factorize: x6 − 729
Ans. x6−729=(x2)3−(9)3
=[x2−9][(x2)2+x2×9+92]
=[x2−32](x4+9x2+81)
=(x+3)(x−3)(x4+18x2+81−9x2)
=(x+3)(x−3)[(x2)2+2×x2×9+92−9x2]
=(x+3)(x−3)[(x2+9)2−(3x)2]
=(x+3)(x−3)(x2+9+3x)(x2+9−3x)
=(x+3)(x−3)(x2+3x+9)(x2−3x+9)
Q.22. Factorise: x9 – y9
Ans. x9–y9=(x3)3−(y3)3
we know
a3−b3=(a−b)(a2+b2+ab)
a=x3,b=y3
So,x9–y9=(x3)3−(y3)3
=(x3−y3)(x6+y6+x3y3)
=(x−y)(x2+y2+xy)(x6+y6+x3y3)
Q.23. Factorize: (a + b)3 − (a − b)3
Ans. (a + b)3−(a−b)3=[(a+b)−(a−b)][(a+b)2+(a+b)(a−b)+(a−b)2]
=(a+b−a+b)[a2+2ab+b2+a2−b2+a2−2ab+b2]
=2b(3a2+b2)
Q.24. Factorize: 8a3 − b3 − 4ax + 2bx
Ans. 8a3−b3−4ax+2bx=[(2a)3−(b)3]−2x(2a−b)
=(2a−b)[(2a)2+2ab+b2]−2x(2a−b)
=(2a−b)(4a2+2ab+b2)−2x(2a−b)
=(2a−b)(4a2+2ab+b2−2x)
Q.25. Factorize: a3 + 3a2b + 3ab2 + b3 − 8
Ans. a3+3a2b+3ab2+b3−8=(a3+b3+3a2b+3ab2)−8
=[a3+b3+3ab(a+b)]−8
=(a+b)3−23
=(a+b−2)[(a+b)2+2(a+b)+22]
=(a+b−2)[(a+b)2+2(a+b)+4]
Q.26. Factorize: a3−1/a3−2a+2/a
Ans. a3−1/a3−2a+2/a=(a3−1/a3)−2(a−1/a)
=[(a)3−(1/a)3]−2(a−1/a)
=(a−1/a)[a2+a×1/a+(1/a)2]−2(a−1/a)
=(a−1/a)(a2+1+1/a2)−2(a−1/a)
=(a−1/a)(a2+1+1/a2−2)
=(a−1/a)(a2−1+1/a2)
Q.27. Factorize: 2a3 + 16b3 − 5a − 10b
Ans. 2a3+16b3−5a−10b=2[a3+8b3]−5(a+2b)
=2[a3+(2b)3]−5(a+2b)
=2(a+2b)[a2−a×2b+(2b)2]−5(a+2b)
=2(a+2b)(a2−2ab+4b2)−5(a+2b)
=(a+2b)[2(a2−2ab+4b2)−5]
Q.28. Factorise: a6 + b6
Ans. a6+b6=(a2)3+(b2)3
=(a2+b2)[(a2)2−a2b2+(b2)2]
=(a2+b2)(a4−a2b2+b4)
Q.29. Factorise: a12 – b12
Ans. a12 – b12
=(a6+b6)(a6−b6)
=[(a2)3+(b2)3][(a3)2−(b3)2]
=[(a2+b2)(a4+b4−a2b2)][(a3−b3)(a3+b3)]
=[(a2+b2)(a4+b4−a2b2)][(a−b)(a2+b2+ab)(a+b)(a2+b2−ab)]
=(a−b)(a2+b2+ab)(a+b)(a2+b2−ab)(a2+b2)(a4+b4−a2b2)
Q.30. Factorise: x6 – 7x3 – 8
Ans. Let x3=y
So, the equation becomes
y2−7y−8=y2−8y+y−8
=y(y−8)+(y−8)
=(y−8)(y+1)
=(x3−8)(x3+1)
=(x−2)(x2+4+2x)(x+1)(x2+1−x)
Q.31. Factorise: x3 – 3x2 + 3x + 7
Ans. x3 – 3x2 + 3x + 7
=x3–3x2+3x+7
=x3–3x2+3x+8−1
=x3–3x2+3x−1+8
=(x3–3x2+3x−1)+8
=(x−1)3+23
=(x−1+2)[(x−1)2+4−2(x−1)]
=(x+1)[x2+1−2x+4−2x+2]
=(x+1)(x2−4x+7)
Q.32. Factorise: (x +1)3 + (x – 1)3
Ans. (x +1)3 + (x – 1)3
=(x+1+x−1)[(x+1)2+(x−1)2−(x−1)(x+1)]
=(2x)[(x+1)2+(x−1)2−(x2−1)]
=2x(x2+1+2x+x2+1−2x−x2+1)
=2x(x2+3)
Q.33. Factorise: (2a +1)3 + (a – 1)3
Ans. (2a +1)3 + (a – 1)3
=(2a+1+a−1)[(2a+1)2+(a−1)2−(2a+1)(a−1)]
=(3a)[4a2+1+4a+a2+1−2a−2a2+2a−a+1]
=3a[3a2+3a+3]
=9a(a2+a+1)
Q.34. Factorise: 8(x +y)3 – 27(x – y)3
Ans. 8(x +y)3 – 27(x – y)3
=[2(x+y)]3−[3(x−y)]3
=(2x+2y−3x+3y)[4(x+y)2+9(x−y)2+6(x2−y2)]
=(−x+5y)[4(x2+y2+2xy)+9(x2+y2−2xy)+6(x2−y2)]
=(−x+5y)[4x2+4y2+8xy+9x2+9y2−18xy+6x2−6y2]
=(−x+5y)(19x2+7y2−10xy)
Q.35. Factorise: (x +2)3 + (x – 2)3
Ans. (x +2)3 + (x – 2)3
=(x+2+x−2)[(x+2)2+(x−2)2−(x2−4)]
=2x(x2+4+4x+x2+4−4x−x2+4)
=2x(x2+12)
Q.36. Factorise: (x + 2)3 – (x – 2)3
Ans. (x + 2)3 – (x – 2)3
=(x+2−x+2)[(x+2)2+(x−2)2+(x2−4)]
=4[x2+4+4x+x2+4−4x+x2−4]
=4(3x2+4)
Q.37. Prove that (0.85×0.85×0.85+0.15×0.15×0.15)/(0.85×0.85−0.85×0.15+0.15×0.15)=1.
Ans. LHS: (0.85×0.85×0.85+0.15×0.15×0.15)/(0.85×0.85−0.85×0.15+0.15×0.15)
=(0.85)3+(0.15)3/(0.85)2−0.85×0.15+(0.15)2
We know a3+b3=(a+b)(a2+b2−ab)
Here a=0.85,b=0.15
(0.85)3+(0.15)3/(0.85)2−0.85×0.15+(0.15)2
=(0.85+0.15)((0.85)2−0.85×0.15+(0.15)2)(0.85)2−0.85×0.15+(0.15)2=0.85+0.15=1:RHS
Thus, LHS = RHS
Q.38. Prove that (59×59×59−9×9×9)/(59×59+59×9+9×9)=50.
Ans. (59×59×59−9×9×9)/(59×59+59×9+9×9)
=(59)3−93/592+59×9+92
We know a3+b3=(a+b)(a2+b2−ab)
Here a=59,b=9
So, ((59−9)(592+92+59×9))/(592+92+59×9)=59−9=50:RHS
Thus, LHS=RHS
RS Aggarwal Solutions: Exercise 3G - Factorisation of Polynomials
Q.1. Find the product: (x + y − z) (x2 + y2 + z2 − xy + yz + zx)
Ans. (x+y−z)(x2+y2+z2−xy+yz+zx)
=[x+y+(−z)][x2+y2+(−z)2−xy−y×(−z)−[−z]×x]
=x3+y3+(−z)3−3x×y×(−z)
=x3+y3−z3+3xyz
Q.2. Find the product: (x – y − z) (x2 + y2 + z2 + xy – yz + xz)
Ans. (x – y − z) (x2 + y2 + z2 + xy – yz + xz)
=(x+(−y)+(−z)) (x2+y2+z2+xy–yz+xz)
We know
(a+b+c)(a2+b2+c2−ab−bc−ca)
=a3+b3+c3−3abc
Here, a=x,b=−y,c=−z
(x+(−y)+(−z)) (x2+y2+z2+xy–yz+xz)
=x3−y3−z3−3xyz
Q.3. Find the product: (x − 2y + 3) (x2 + 4y2 + 2xy − 3x + 6y + 9)
Ans. (x − 2y + 3)(x2+4y2+2xy−3x+6y+9)
=(x − 2y + 3)(x2+4y2+9+2xy+6y−3x)
=[x+(−2y)+3][x2+(−2y)2+(3)2−x×(−2y)−(−2y)×3−3×x]
=(x)3+(−2y)3+(3)3−3(x)(−2y)(3)
=x3−8y3+27+18xy
Q.4. Find the product: (3x – 5y + 4) (9x2 + 25y2 + 15xy − 20y + 12x + 16)
Ans. (3x−5y+4)(9x2+25y2+15xy−20y+12x+16)
=(3x+(−5y)+4)(9x2+25y2+16+15xy−20y+12x)
(a+b+c)(a2+b2+c2−ab−bc−ca)
=a3+b3+c3−3abc
Here, a=3x,b=−5y,c=4
(3x+(−5y)+4)(9x2+25y2+16+15xy−20y+12x)
=(3x)3+(−5y)3+43−3×3x(−5y)(4)
=27x3−125y3+64+180xy
Q.5. Factorize: 125a3 + b3 + 64c3 − 60abc
Ans. 125a3+b3+64c3−60abc=(5a)3+(b)3+(4c)3−3×5a×b×4c
=(5a+b+4c)[(5a)2+(b)2+(4c)2−5a×b−b×4c−5a×4c]
=(5a+b+4c)(25a2+b2+16c2−5ab−4bc−20ac)
Q.6. Factorize: a3 + 8b3 + 64c3 − 24abc
Ans. a3+8b3+64c3−24abc=a3+(2b)3+(4c)3−3×a×2b×4c
=(a+2b+4c)[a2+(2b)2+(4c)2−a×2b−2b×4c−4c×a]
=(a+2b+4c) (a2+4b2+16c2-2ab-8bc-4ca)
Q.7. Factorize: 1 + b3 + 8c3 − 6bc
Ans. 1+b3+8c3−6bc=(1)3+(b)3+(2c)3−3×1×b×2c
=(1+b+2c)[12+b2+(2c)2−1×b−b×2c−1×2c]
=(1+b+2c)(1+b2+4c2−b−2bc−2c)
Q.8. Factorize: 216 + 27b3 + 8c3 − 108abc
Ans. 216+27b3+8c3−108abc
=(6)3+(3b)3+(2c)3−3×6×3b×2c
=(6+3b+2c)[62+(3b)2+(2c)2−6×3b−3b×2c−2c×6]
=(6+3b+2c)(36+9b2+4c2−18b−6bc−12c)
Q.9. Factorize: 27a3 − b3 + 8c3 + 18abc
Ans. 27a3−b3+8c3+18abc=(3a)3+(−b)3+(2c)3−3×(3a)×(−b)×(2c)
=[3a+(−b)+2c][(3a)2+(−b)2+(2c)2−3a(−b)−(−b)2c−3a×2c]
=(3a−b+2c)(9a2+b2+4c2+3ab+2bc−6ac)
Q.10. Factorize: 8a3 + 125b3 − 64c3 + 120abc
Ans. 8a3+125b3−64c3+120abc=(2a)3+(5b)3+(−4c)3−3×(2a)×(5b)×(−4c)
=(2a+5b−4c)[(2a)2+(5b)2+(−4c)2−(2a)(5b)−(5b)(−4c)−(2a)×(−4c)]
=(2a+5b−4c)(4a2+25b2+16c2−10ab+20bc+8ac)
Q.11. Factorize: 8 − 27b3 − 343c3 − 126bc
Ans. 8−27b3−343c3−126bc
=(2)3+(−3b)3+(−7c)3−3×(2)×(−3b)×(−7c)
=[2+(−3b)+(−7c)][(2)2+(−3b)2+(−7c)2−(2)(−3b)−(−3b)(−7c)−(2)(−7c)]
=(2−3b−7c)(4+9b2+49c2+6b−21bc+14c)
Q.12. Factorize: 125 − 8x3 − 27y3 − 90xy
Ans. 125−8x3−27y3−90xy=53+(−2x)3+(−3y)3−3×5×(−2x)×(−3y)
=[5+(−2x) +(−3y)][52+(−2x)2+(−3y)2−5×(−2x)−(−2x)(−3y)−5×(−3y)] =(5−2x−3y)(25+4x2+9y2+10x−6xy+15y)
Q.13. Factorize: 2√2a3 + 16√2b3+c3−12abc
Ans. 2√2a3+16√2b3+c3−12abc
=(√2a)3+(2√2b)3+c3−3×(√2a)×(2√2b)×(c)
=(√2a+2√2b+c)[(√2a)2+(2√2b)2+c2−(√2a)×(2√2b)−(2√2b)×(c)−(2√a)×(c)]
=(√2a+2√2b+c)(2a2+8b2+c2−4ab−2√2bc−√2ac)
Q.14. Factorise: 27x3 – y3 – z3 – 9xyz
Ans. 27x3−y3–z3–9xyz
=(3x)3−y3−z3−3×(3x)×(−y)×(−z)
We know,
a3+b3+c3−3abc
=(a+b+c)(a2+b2+c2−ab−bc−ca)
a=3x,b=−y,c=−z
(3x)3−y3−z3−3×(3x)×(−y)×(−z)
=(3x−y−z)(9x2+y2+z2+3xy−yz+3xz)
Q.15. Factorise: 2√2a3+3√3b3+c3−3√6abc
Ans. 2√2a3+3√3b3+c3−3√6abc
=(√2a)3+(√3b)3+c3−3(√2a)(√3b)c
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x=√2a,y=√3b,z=c
(√2a)3+(√3b)3+c3−3(√2a)(√3b)c
=(√2a+√3b+c)(2a2+3b2+c2−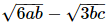
- √2ac)
Q.16. Factorise: 3√3a3−b3−5√5c3−3√15abc
Ans. 3√3a3−b3−5√5c3−3√15abc
=(√3a)3+(−b)3+(−√5c)3−3(√3a)(−b)(−√5c)
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
Here, x=(√3a),y=(−b),z=(−√5c)
3√3a3−b3−5√5c3−3√15abc
=(√3a)3+(−b)3+(−√5c)3−3(√3a)(−b)(−√5c)
=(√3a−b−√5c)(3a2+b2+5c2+√3ab−√5bc+√15c)
Q.17. Factorize: (a − b)3 + (b − c)3 + (c − a)3
Ans. (a−b)3+(b−c)3+(c−a)3
Putting (a−b)=x, (b−c)=y and (c−a)=z, we get:
(a−b)3+(b−c)3+(c−a)3
=x3+y3+z3[Where (x+y+z)=(a−b)+(b−c)+(c−a)=0]
=3xyz [(x+y+z)=0 ⇒x3+y3+z3=3xyz]
=3(a−b)(b−c)(c−a)
Q.18. Factorise: (a−3b)3+(3b−c)3+(c−a)3
Ans. We know x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x3+y3+z3=(x+y+z)(x2+y2+z2−xy−yz−zx)+3xyz
Here, x=(a−3b),y=(3b−c),z=(c−a)
(a−3b)3+(3b−c)3+(c−a)3
=(a−3b+3b−c+c−a)[(a−3b)2+(3b−c)2+(c−a)2−(a−3b)(3b−c)−(3b−c)(c−a)−(c−a)(a−3b)]+3(a−3b)(3b−c)(c−a)
=0+3(a−3b)(3b−c)(c−a)
=3(a−3b)(3b−c)(c−a)
Q.19. Factorize: (3a − 2b)3 + (2b − 5c)3 + (5c − 3a)3
Ans. Put (3a−2b)=x, (2b−5c)=y and (5c−3a)=z.
We have:
x+y+z = 3a−2b+2b−5c+5c−3a=0
Now,(3a−2b)3+(2b−5c)3+(5c−3a)3=x3+y3+z3
=3xyz [Here, x+y+z=0. So, x3 + y3 +z3 = 3xyz]
=3(3a−2b)(2b−5c)(5c−3a)
Q.20. Factorize: (5a − 7b)3 + (9c − 5a)3 + (7b − 9c)3
Ans. Put (5a−7b)=x, (9c−5a)=z and (7b−9c)=y.
Here, x+y+z = 5a − 7b + 9c−5a+7b−9c=0
Thus, we have:
(5a−7b)3+(9c−5a)3+(7b−9c)3=x3+z3+y3
=3xzy [When x+y+z=0, x3+y3+z3 = 3xyz.]
=3 (5a−7b)(9c−5a)(7b−9c)
Q.21. Factorize: a3(b − c)3 + b3(c − a)3 + c3(a − b)3
Ans. We have: a3(b−c)3+b3(c−a)3+c3(a−b)3 = [a(b−c)]3+[b(c−a)]3+[c(a−b)]3
Put a(b−c) = x
b(c−a) = y
c(a−b) = z
Here, x+y+z = a(b−c)+b(c−a)+c(a−b)
=ab − ac + bc − ab + ac − bc
=0
Thus, we have:
a3(b−c)3+b3(c−a)3+c3(a−b)3 =x3 + y3+ z3
=3xyz [When x+y+z =0, x3 + y3+ z3 =3xyz.]
=3 a(b−c)b(c−a)c(a−b)
=3abc(a−b)(b−c)(c−a)
Q.22. Evaluate
(i) (–12)3 + 73 + 53
(ii) (28)3 + (–15)3 + (–13)3
Ans. (i) (–12)3 + 73 + 53
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x3+y3+z3=(x+y+z)(x2+y2+z2−xy−yz−zx)+3xyz
Here, x=(−12),y=7,z=5
(−12)3+73+53
=(−12+7+5)[(−12)2+72+52−7(−12)−35+60]+3(−12)×35
=0−1260
= -1260
(ii) (28)3 + (–15)3 + (–13)3
We know
x3+y3+z3−3xyz=(x+y+z)(x2+y2+z2−xy−yz−zx)
x3+y3+z3=(x+y+z)(x2+y2+z2−xy−yz−zx)+3xyz
Here, x=(−28),y=−15,z=−13
(28)3+(−15)3+(−13)3
=(28−15−13)[(28)2+(−15)2+(−13)2−28(−15)−(−15)(−13)−28(−13)]+3×28(−15)(−13)
=0+16380=16380
Q.23. Prove that (a+b+c)3−a3−b3−c3=3(a+b) (b+c) (c+a)
Ans. (a+b+c)3=[(a+b)+c]3
= (a+b)3+c3+3(a+b)c(a+b+c)
⇒(a+b+c)3=a3+b3+3ab(a+b)+c3+3(a+b)c(a+b+c)
⇒(a+b+c)3−a3+b3−c3=3ab(a+b)+3(a+b)c(a+b+c)
⇒(a+b+c)3−a3+b3−c3=3(a+b)[ab+ca+cb+c2]
⇒(a+b+c)3−a3+b3−c3=3(a+b)[a(b+c)+c(b+c)]
⇒(a+b+c)3−a3+b3−c3=3(a+b)(b+c)(a+c)
Q.24. If a, b, c are all nonzero and a + b + c = 0, prove that a2/bc+b2/ca+c2/ab=3.
Ans. a+b+c=0
⇒a3+b3+c3=3abc
Thus, we have:
(a2/bc+b2/ca+c2/ab)=(a3+b3+c3)/abc
=3abc/abc
=3
Q.25. If a + b + c = 9 and a2 + b2 + c2 = 35, find the value of (a3 + b3 + c3 – 3abc).
Ans. a + b + c = 9
⇒(a+b+c)2=92=81
⇒a2+b2+c2+2(ab+bc+ca)=81
⇒35+2(ab+bc+ca)=81
⇒(ab+bc+ca)=23
We know,
(a3 + b3 + c3 – 3abc)
= (a+b+c)(a2+b2+c2−ab−bc−ca)
=(9)(35−23)
=108
|
44 videos|412 docs|54 tests
|
FAQs on RS Aggarwal Solutions: Factorisation of Polynomials- 2 - Mathematics (Maths) Class 9
| 1. What is the importance of factorisation of polynomials? |  |
| 2. How can I factorise a polynomial expression? | |
| 3. Can all polynomials be factorised? | |
| 4. What is the role of factorisation in solving quadratic equations? | |
| 5. Can factorisation be used to simplify fractions with polynomial expressions? | |
|
4.85/5 Rating |
|
Dec 27, 2024 Last updated |
|
Explore Courses for Class 9 exam
|
|
Objective type Questions
,Free
,RS Aggarwal Solutions: Factorisation of Polynomials- 2 | Mathematics (Maths) Class 9
,Semester Notes
,RS Aggarwal Solutions: Factorisation of Polynomials- 2 | Mathematics (Maths) Class 9
,Previous Year Questions with Solutions
,Summary
,Exam
,MCQs
,practice quizzes
,Viva Questions
,Extra Questions
,Sample Paper
,video lectures
,study material
,mock tests for examination
,shortcuts and tricks
,ppt
,RS Aggarwal Solutions: Factorisation of Polynomials- 2 | Mathematics (Maths) Class 9
,Important questions
,past year papers
,
RS Aggarwal Solutions: Factorisation of Polynomials- 2 Free PDF Download
Importance of RS Aggarwal Solutions: Factorisation of Polynomials- 2
RS Aggarwal Solutions: Factorisation of Polynomials- 2 Notes
RS Aggarwal Solutions: Factorisation of Polynomials- 2 Class 9 Questions
Study RS Aggarwal Solutions: Factorisation of Polynomials- 2 on the App
|
© EduRev
|
Education Revolution
|
|
