RS Aggarwal Exercise 1.1 Number System
Q.1. Is zero a rational number? Justify.
Ans. Yes, 0 is a rational number.
0 can be expressed in the form of the fraction p/q,where p = 0 and q c an be any integer except 0.
Q.2. Represent each of the following rational number line:
(i) 5/7
(ii) 8/3
(iii)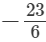
(iv) 1.3
(v) - 2.4
Ans.
(i) 5/7
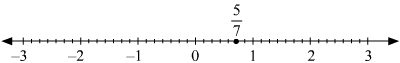
(ii) 8/3
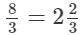
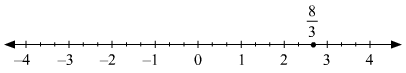
(iii)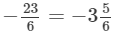
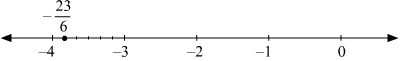
(iv) 1.3
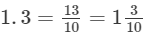
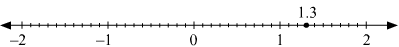
(v) – 2.4
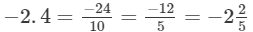
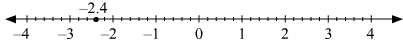
Q.3. Find a rational number between
(i) 3/8 and 2/5
(ii) 1.3 and 1.4
(iii) −1 and 1/2
(iv) 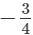 and
and 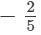
(v) 1/9 and 2/9
Ans. (i) 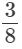 and
and 
Let:
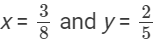
Rational number lying between x and y:
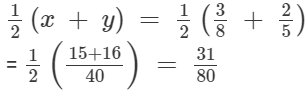
(ii) 1.3 and 1.4
Let:
x = 1.3 and y = 1.4
Rational number lying between x and y:
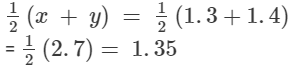
(iii) −1 and 1/2
Let:
x = -1 and y = 1/2
Rational number lying between x and y:
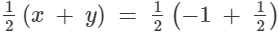

(iv) 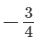 and
and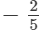
Let:
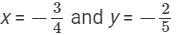
Rational number lying between x and y:
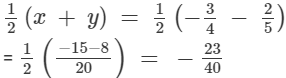
(v) 1/9 and 2/9
A rational number lying between 1/9 and 2/9 will be
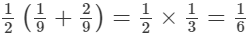
Q.4. Find three rational numbers lying between 3/5 and 7/8. How many rational numbers can be determined between these two numbers?
Ans.
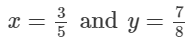
n = 3
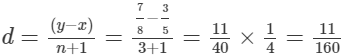
Rational numbers between 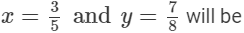
(x + d),(x + 2d),...,(x + nd)
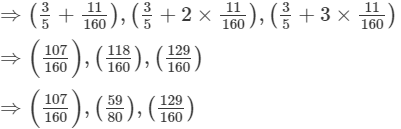
There are infinitely many rational numbers between two given rational numbers.
Q.5.
Find four rational numbers between 3/7 and 5/7.
Ans.
n = 4
n + 1 = 4 + 1 = 5
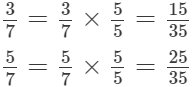
Thus, rational numbers between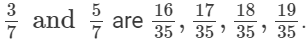
Q.6.
Find six rational numbers between 2 and 3.
Ans. x = 2, y = 3 and n = 6
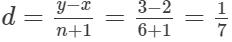
Thus, the required numbers are
(x + d),(x + 2d),(x + 3d),...,(x + nd)
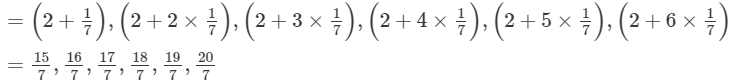
Q.7.
Find five rational numbers between 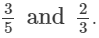
Ans.
n = 5
n + 1 = 6
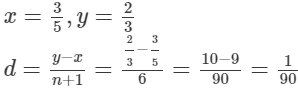
Thus, rational numbers between will  be
be
(x + d),(x + 2d),(x + 3d),(x + 4d),(x + 5d)
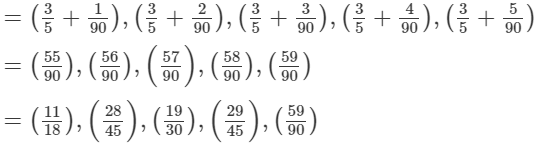
Q.8.
Insert 16 rational numbers between 2.1 and 2.2.
Ans.
Let:
x = 2.1, y = 2.2 and n = 16
We know:
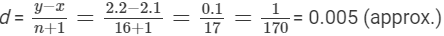
So, 16 rational numbers between 2.1 and 2.2 are:
(x + d), (x + 2d), ...(x + 16d)
= [2.1 + 0.005], [2.1 + 2(0.005)],...[2.1 + 16(0.005)]
= 2.105, 2.11, 2.115, 2.12, 2.125, 2.13, 2.135, 2.14, 2.145, 2.15, 2.155, 2.16, 2.165, 2.17,
2.175 and 2.18
Q.9. State whether the following statements are true or false. Give reasons for your answer.
(i) Every natural number is a whole number.
(ii) Every whole number is a natural number.
(iii) Every integer is a whole number.
(iv) Every integer is a rational number.
(v) Every rational number is an integer.
(vi) Every rational number is a whole number.
Ans.
(i) Every natural number is a whole number.
True, since natural numbers are counting numbers i.e N = 1, 2,...
Whole numbers are natural numbers together with 0. i.e W = 0, 1, 2,...
So, every natural number is a whole number
(ii) Every whole number is a natural number.
False, as whole numbers contain natural numbers and 0 whereas natural numbers only contain the counting numbers except 0.
(iii) Every integer is a whole number.
False, whole numbers are natural numbers together with a zero whereas integers include negative numbers also.
(iv) Every integer is a rational number.
True, as rational numbers are of the form 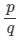 where q ≠ 0. All integers can be represented in the form p/q where q ≠ 0.
where q ≠ 0. All integers can be represented in the form p/q where q ≠ 0.
(v) Every rational number is an integer.
False, as rational numbers are of the form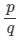 where q ≠ 0. Integers are negative and positive numbers which are not in p/q form. For example, 1/2 is a rational number but not an integer.
where q ≠ 0. Integers are negative and positive numbers which are not in p/q form. For example, 1/2 is a rational number but not an integer.
(vi) Every rational number is a whole number.
False, as rational numbers are of the form p/q where q ≠ 0. Whole numbers are natural numbers together with a zero.
For example, 5/7 is a rational number but not a whole number.
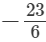
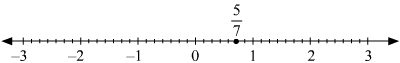
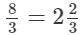
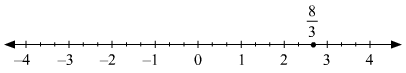
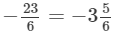
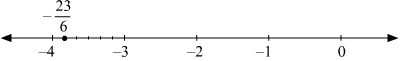
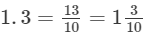
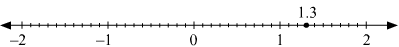
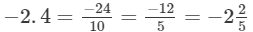
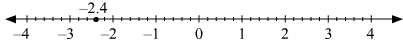
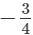 and
and 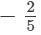
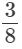 and
and 
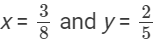
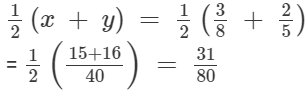
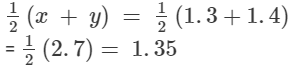
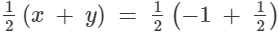

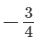 and
and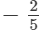
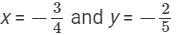
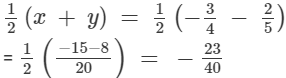
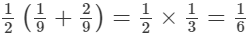
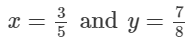
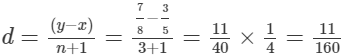
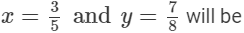
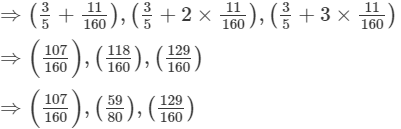
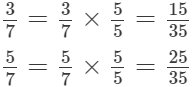
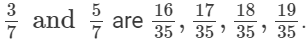
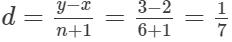
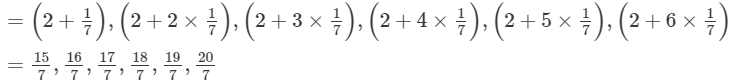
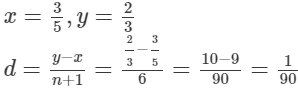
 be
be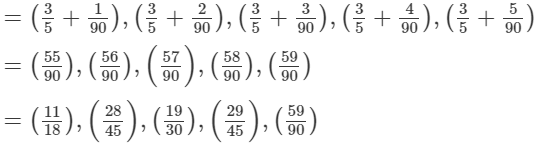
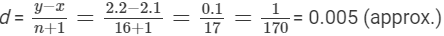
 where q ≠ 0. All integers can be represented in the form p/q where q ≠ 0.
where q ≠ 0. All integers can be represented in the form p/q where q ≠ 0. where q ≠ 0. Integers are negative and positive numbers which are not in p/q form. For example, 1/2 is a rational number but not an integer.
where q ≠ 0. Integers are negative and positive numbers which are not in p/q form. For example, 1/2 is a rational number but not an integer.


























