RS Aggarwal Solutions: Number System- 2 | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| RS Aggarwal Exercise 1.2 Number System |

|
| RS Aggarwal Exercise 1.3 Number System |

|
| RS Aggarwal Exercise 1.4 Number System |

|
| RS Aggarwal Exercise 1.5 Number System |

|
RS Aggarwal Exercise 1.2 Number System
Q.1. Write actual division, find which of the following rational numbers are terminating decimals.
(i) 13/80
(ii) 7/24
(iii) 5/12
(iv) 31/375
(v) 16/125
Ans.
(i) 13/80
Denominator of 13/80 is 80.
And,
80 = 24×5
Therefore, 80 has no other factors than 2 and 5.
Thus, 13/80 is a terminating decimal.
(ii) 7/24
Denominator of 7/24 is 24.
And,
24 = 23×3
So, 24 has a prime factor 3, which is other than 2 and 5.
Thus, 7/24 is not a terminating decimal.
(iii) 5/12
Denominator of 5/12 is 12.
And,
12 = 22×3
So, 12 has a prime factor 3, which is other than 2 and 5.
Thus, 5/12 is not a terminating decimal.
(iv) 31/375
Denominator of 31/375 is 375.
375 = 53×3
So, the prime factors of 375 are 5 and 3.
Thus, 31/375 is not a terminating decimal.
(v) 16/125
Denominator of 16/125 is 125.
And,
125 = 53
Therefore, 125 has no other factors than 2 and 5.
Thus, 16/125 is a terminating decimal.
Question 2:
Write each of the following in decimal form and say what kind of decimal expansion each has.
(i) 5/8
(ii) 7/25
(iii) 3/11
(iv) 5/13
(v) 11/24
(vi) 261/400
(vii) 231/625
(viii) 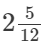
Ans. (i) 5/8 = 0.625
By actual division, we have: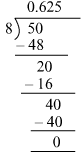
It is a terminating decimal expansion.
(ii) 7/25
7/25 = 0.28
By actual division, we have: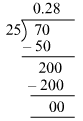
It is a terminating decimal expansion.
(iii) 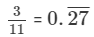
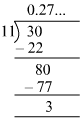
It is a non-terminating recurring decimal.
(iv) 
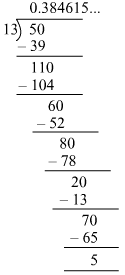
It is a non-terminating recurring decimal.
(v) 11/24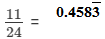
By actual division, we have: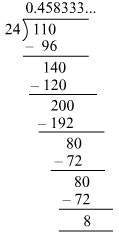
It is nonterminating recurring decimal expansion.
(vi) 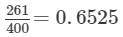
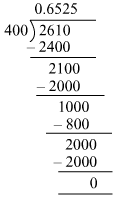
It is a terminating decimal expansion.
(vii) 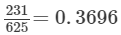
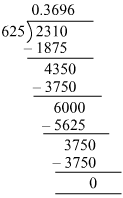
It is a terminating decimal expansion.
(viii)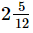
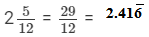
By actual division, we have: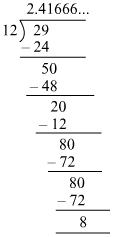
It is non-terminating decimal expansion.
Q.3.
Express each of the following decimals in the form p/q, where p, q are integers and q ≠ 0.
(i)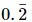
(ii)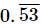
(iii)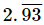
(iv)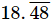
(v)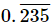
(vi)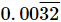
(vii)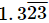
(viii)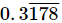
(ix)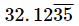
(x)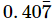
Ans.
(i) 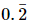
Let x = 0.222... .....(i)
Only one digit is repeated so, we multiply x by 10.
10x = 2.222... .....(ii)
Subtracting (i) from (ii) we get
9x = 2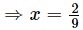
(ii)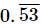
Let x = 0.5353... .....(i)
Two digits are repeated so, we multiply x by 100.
100x = 53.5353... .....(ii)
Subtracting (i) from (ii) we get
99x = 53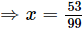
(iii)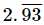
Let x = 2.9393... .....(i)
Two digits are repeated so, we multiply x by 100.
100x = 293.9393... .....(ii)
Subtracting (i) from (ii) we get
99x = 291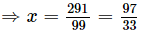
(iv)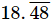
Let x = 18.4848... .....(i)
Two digits are repeated so, we multiply x by 100.
100x = 1848.4848... .....(ii)
Subtracting (i) from (ii) we get
99x = 1830
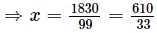
(v)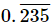
Let x = 0.235235... .....(i)
Three digits are repeated so, we multiply x by 1000.
1000x = 235.235235... .....(ii)
Subtracting (i) from (ii) we get
999x = 235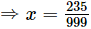
(vi)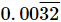
Let x = 0.003232... .....(i)
we multiply x by 100.
100x = 0.3232... .....(ii)
Again multiplying by 100 as there are 2 repeating numbers after decimals we get
10000x = 32.3232... .....(iii)
Subtracting (ii) from (iii) we get
9900x = 32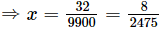
(vii)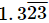
Let x = 1.32323... .....(i)
we multiply x by 10.
10x = 13.2323... .....(ii)
Again multiplying by 100 as there are 2 repeating numbers after decimals we get
1000x = 1323.2323... .....(iii)
Subtracting (ii) from (iii) we get
990x=1310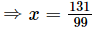
(viii)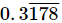
Let x = 0.3178178... .....(i)
we multiply x by 10.
10x = 3.178178... .....(ii)
Again multiplying by 1000 as there are 3 repeating numbers after decimals we get
10000x = 3178.178178... .....(iii)
Subtracting (ii) from (iii) we get
9990x = 3175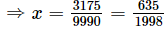
(ix)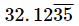
Let x = 32.123535... .....(i)
we multiply x by 100.
100x = 3212.3535... .....(ii)
Again multiplying by 100 as there are 2 repeating numbers after decimals we get
10000x = 321235.35... .....(iii)
Subtracting (ii) from (iii) we get
9900x=318023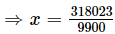
(x)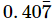
Let x = 0.40777... .....(i)
we multiply x by 100.
100x = 40.7777... .....(ii)
Again multiplying by 10 as there is 1 repeating number after decimals we get
1000x = 407.777... .....(iii)
Subtracting (ii) from (iii) we get
900x = 367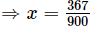
Q.4. Express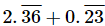 as a fraction in simplest form.
as a fraction in simplest form.
Ans.
Given: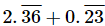
Let
First we take x and convert it into p/q
100x = 236.3636... ...(iii)
Subtracting (i) from (iii) we get
99x=234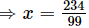
Similarly, multiply y with 100 as there are 2 decimal places which are repeating themselves.
100y = 23.2323... ...(iv)
Subtracting (ii) from (iv) we get
99y = 23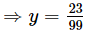
Adding x and y we get
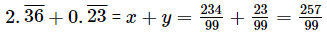
Q.5. Express in the form of p/q 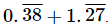
Ans.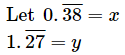
x = 0.3838... ...(i)
Multiply with 100 as there are 2 repeating digits after decimals
100x = 38.3838... ...(ii)
Subtracting (i) from (ii) we get
99x = 38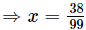
Similarly, we take
y = 1.2727... ...(iii)
Multiply y with 100 as there are 2 repeating digits after decimal.
100y = 127.2727... ...(iv)
Subtract (iii) from (iv) we get
99y = 126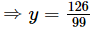
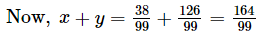
RS Aggarwal Exercise 1.3 Number System
Q.1. What are irrationl numbers? How do they differ from rational numbers? Give examples.
Ans. A number that can neither be expressed as a terminating decimal nor be expressed as a repeating decimal is called an irrational number. A rational number, on the other hand, is always a terminating decimal, and if not, it is a repeating decimal.
Examples of irrational numbers:
0.101001000...
0.232332333...
Q.2. Classify the following numbers as rational or irrational. give reasons to support your answer.
(i) 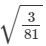
(ii)
(iii)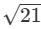
(iv)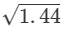
(v)
(vi) 4.1276
(vii) 22/7
(viii) 1.232332333..
(ix) 3.040040004....
(x) 2.356565656...
(xi) 6.834834...
Ans. 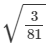
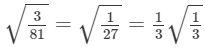
It is an irrational number.
(ii) = 19
= 19
So, it is rational.
(iii)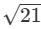
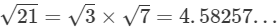
It is an irrational number.
(iv)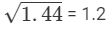
So, it is rational.
(v) 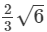
It is an irrational number
(vi) 4.1276
It is a terminating decimal. Hence, it is rational.
(vii) 22/7
22/7 is a rational number because it can be expressed in the p/q form.
(viii) 1.232332333...is an irrational number because it is a non−terminating, non−repeating decimal.
(ix) 3.040040004... is an irrational number because it is a non−terminating, non−repeating decimal.
(x) 2.356565656... is a rational number because it is repeating.
(xi) 6.834834... is a rational number because it is repeating.
Q.3. Let x be a rational number and y be an irrational number. Is x + y necessarily an irrational number? Give a example in support of your answer.
Ans.
x be a rational number and y be an irrational number then x + y necessarily will be an irrational number.
Example: 5 is a rational number but √2 is irrational.
So, 5 + √2 will be an irrational number.
Q.4. Let a be a rational number and b be an irrational number. Is ab necessarily an irrational number? Justify your answer with an example.
Ans. a be a rational number and b be an irrational number then ab necessarily will be an irrational number.
Example: 6 is a rational number but √5 is irrational. And 6√5 is also an irrational number.
Q.5. Is the product of two irrationals always irrational? Justify your answer.
Ans. Product of two irrational numbers is not always an irrational number.
Example: √5 is irrational number. And √5 × √5 = 5 is a rational number. But the product of another two irrational numbers √2 and √3 is √6 which is also an irrational numbers.
Q.6. Give an example of two irrational numbers whose
(i) difference is an irrational number.
(ii) difference is a rational number.
(iii) sum is an irrational number.
(iv) sum is a rational number.
(v) product is an irrational number.
(vi) product is a rational number.
(vii) quotient is an irrational number.
(viii) quotient is a rational number.
Ans.
(i) 2 irrational numbers with difference an irrational number will be 3−√5 and 3+√5.
(ii) 2 irrational numbers with difference is a rational number will be 5+√3 and 2+√3
(iii) 2 irrational numbers with sum an irrational number 7+√5 and √6 − 8
(iv) 2 irrational numbers with sum a rational number is 3−√2 and 3 + √2
(v) 2 irrational numbers with product an irrational number will be 6 + √3 and 7−√3
(vi) 2 irrational numbers with product a rational number will be (5 + √7) and (5 − √7)
(vii) 2 irrational numbers with quotient an irrational number will be √15 and √5
(viii) 2 irrational numbers with quotient a rational number will be √63 and √7.
Question 7: Examine whether the following numbers are rational or irrational.
(i) 3 + √3
(ii) √7 − 2
(iii)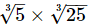
(iv) 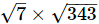
(v) 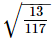
(vi) √8 × √2
Ans. (i) Let us assume, to the contrary, that 3 + √3 is rational.
Then, 3+√3 = pq, where p and q are coprime and q ≠ 0.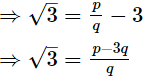
Since, p and q are are integers.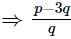 is rational.
is rational.
So, √3 is also rational.
But this contradicts the fact that √3 is irrational.
This contradiction has arisen because of our incorrect assumption that 3 + √3 is rational.
Hence, 3 + √3 is irrational.
(ii) Let us assume, to the contrary, that √7−2 is rational.
Then, √7 − 2 = p/q, where p and q are coprime and q ≠ 0.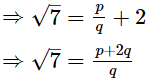
Since, p and q are are integers. is rational.
is rational.
So, √7 is also rational.
But this contradicts the fact that √7 is irrational.
This contradiction has arisen because of our incorrect assumption that √7 − 2 is rational.
Hence, √7 − 2 is irrational.
(iii) As,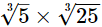
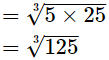
= 5, which is an integer
Hence, 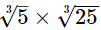 is rational.
is rational.
(iv) As, 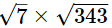
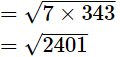
= 49, which is an integer
Hence, 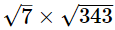 is rational.
is rational.
(v) As,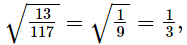 which is rational
which is rational
Hence, 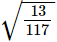 is rational.
is rational.
(vi) As, √8 × √2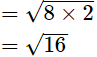
= 4, which is an integer
Hence, √8 × √2 is rational.
Q.8. Insert a rational and an irrational number between 2 and 2.5.
Ans. As, few rational numbers between 2 and 2.5 are: 2.1, 2.2, 2.3, 2.4, ...
And,
Since, 2 = √4 and 2.5= 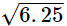
So, irrational number between 2 ans 2.5 are: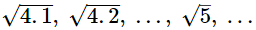
Hence, a rational and an irrational number can be 2.1 and √5, respectively.
Disclaimer: There are infinite rational and irrational numbers between any two rational numbers.
Q.9. How many irrational numbers lie between √2 and √3? Find any three irrational numbers lying between √2 and √3.
Ans. There are infinite number of irrational numbers lying between √2 and √3.
As, √2 = 1.414 and √3 = 1.732
So, the three irrational numbers lying between √2 and √3 are:
1.420420042000..., 1.505005000... and 1.616116111...
Q.10. Find two rational and two irrational number between 0.5 and 0.55.
Ans. The two rational numbers between 0.5 and 0.55 are: 0.51 and 0.52
The two irrational numbers between 0.5 and 0.55 are: 0.505005000... and
0.5101100111000...
Disclaimer: There are infinite number of rational and irrational numbers between 0.5 and 0.55.
Q.11. Find three different irrational numbers between the rational numbers 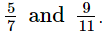
Ans. As, 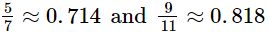
So, the three different irrational numbers are: 0.72020020002..., 0.7515511555111... and 0.808008000...
Disclaimer: There are an infinite number of irrational numbers between two rational numbers.
Q.12. Find two rational numbers of the form p/q between the numbers 0.2121121112... and 0.2020020002... .
Ans. The rational numbers between the numbers 0.2121121112... and 0.2020020002... are:
Disclaimer: There are an infinite number of rational numbers between two irrational numbers.
Q.13. Find two irrational numbers between 0.16 and 0.17.
Ans. The two irrational numbers between 0.16 and 0.17 are 0.161161116... and 0.1606006000...
Disclaimer: There are an infinite number of irrational numbers between two rational numbers.
Q.14. State in each case, whether the given statement is true of false.
(i) The sum of two rational numbers is rational.
(ii) The sum of two irrational numbers is irrational.
(iii) The product of two rational numbers is rational.
(iv) The product of two irrational number is irrational.
(v) The sum of a rational number and an irrational number is irrational.
(vi) The product of a nonzero rational number and an irrational number is a rational number.
(vii) Every real number is rational.
(viii) Every real number is either rational or irrational.
(ix) π is irrational and 22/7 is rational.
Ans.
(i) True
(ii) False
Example: (2 + √3) + (2 − √3) = 4
Here, 4 is a rational number.
(iii) True
(iv) False
Example: √ 3× √3=3
Here, 3 is a rational number.
(v) True
(vi) False
Example: (4)×√5 = 4√5
Here, 4√5 is an irrational number.
(vii) False
Real numbers can be divided into rational and irrational numbers.
(viii) True
(ix) True
RS Aggarwal Exercise 1.4 Number System
Q.1. Add:
(i) (2√3 − 5√2) and (√3+2√2)
(ii) (2√2 + 5√3 − 7√5)and(3√3 − √2 + √5)
(iii)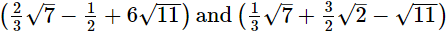
Ans.
(i) 2√3 − 5√2 + √ 3 + 2√2
= (2√3 + √3) + (2√2 − 5√2)
= 3√3− 3√2
(ii) 2√2+ 5√3 − 7√5 + 3√3 − √2 + √5
= 2√2 - √2 + 5√3 + 3√3 + √5 − 7√5
= √2 + 8√3 −6√5
(iii) 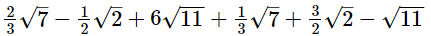
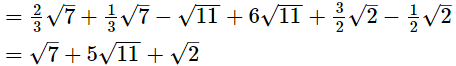
Q.2. Multiply:
(i) 3√5 by 2√5
(ii) 6√15 by 4√3
(iii) 2√6 by 3√3
(iv) 3√8 by 3√2
(v) √10 by √40
(vi) 3√28 by 2√7
Ans.
(i) 3√5 × 2√5 = 3 × 2 × √5 x √5 = 6 × 5 = 30
(ii) 6√15 × 4√3 = 6 × 4 × √5 × √3 × √3 = 24 × 3 × √5 = 72√5
(iii) 2√6 × 3√3 = 2 × 3 × √2 × √3 × √3 = 6 × 3 × √2 = 18√2
(iv) 3√8 × 3√2 = 3 × 3 × √2 × √2 × √2 × √2 = 9 × 4 = 36
(v) √10 × √40 = √2 × √5 × √2 × √2 × √2 × √5 = √2 × √2 × √2 × √2 × √5 × √5 = 2 × 2 × 5 = 20
(vi) 3√28 × 2√7 = 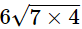 × √7 = 6 × 7 × √4 = 42 × 2 = 84
× √7 = 6 × 7 × √4 = 42 × 2 = 84
Q.3. Divide:
(i) 16√6 by 4√2
(ii) 12√5 by 4√3
(iii) 18√21 by 6√7
Ans.
(i) 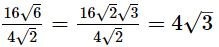
(ii)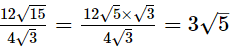
(iii)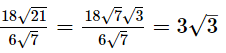
Q.4. Simplify
(i) (3 − √11) (3 + √11)
(ii) (−3 + √5) (−3 − √5)
(iii) (3 − √3)2
(iv) (√5 − √3)2
(v) (5 + √7) (2 + √5)
(vi) (√5 – √2) (√2 - √3)
Ans. (i) (3 − √11) (3 + √11)
=32 − (√11)2 [(a − b)( a + b) =a2 − b2]
=9 − 11
= −2
(ii) (−3 + √5) (−3 − √5)
=(−3)2−(√5)2 [(a + b)(a − b) = a2 − b2]
=9 − 5
=4
(iii) (3 − √3)2
=32+(√3)2 − 2 × 3 × √3 [(a−b)2=a2+b2−2ab]
=9 + 3 − 6√3
=12 − 6√3
(iv) (√5 − √3)2
=(√5)2+ (√3)2 − 2 × √5√3 [(a−b)2 = a2 + b2 − 2ab]
=5 + 3 − 2√15 = 8 − 2√15
= √5 × √2 − √5 × √3 - √2 × √2 + √2 × √3
= √10 − √15 − 2 + √6
(v) (5 + √7) (2 + √5)
(5 + √7) (2 + √5)
= 5 × 2 + 5 × √5+ √7 × 2 +√7 × √5
=10 + 5√5 + 2√7 + 3√5
(vi) (√5 − √2) (√2 − √3)
(√5 - √2)(√2 − √3)
= √5 × √2 – √5 × √3 − √2 × √2 + √2 × √3
= √10 − √15 − 2 + √6
Q.5. Simplify (3 + √3) (2 + √2)2.
Ans. (3 + √3) (2+√2)2
= (3 + √3) [22+(√2)2 + 2 × 2√2]
=(3 + √3) [4 + 2 + 4√2]
= (3 + √3) [6 + 4√2]
=3 × 6 + 3 × 4√2 + √3 × 6 + √3 × 4√2
=18 + 12√2 + 6√3 + 4√6
Q.6. Examine whether the following numbers are rational or irrational:
(i) (5 − √5) (5 + √5)
(ii) (√3 + 2)2
(iii)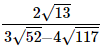
(iv) √8 + 4√32 − 6√2
Ans. (i) (5 − √5) (5 + √5)
=52 − (√5)2 [(a − b)(a + b) = a2 − b2]
= 25 − 5
= 20, which is an integer
Hence, (5 − √5) (5 + √5) is rational.
(ii) (√3 + 2)2
= (√3)2+22+2×√3×2 [(a + b)2=a2 + b2 + 2ab]
= 3 + 4 + 4√3
= 7 + 4√3
Since, the sum and product of rational numbers and an irrational number is always an irrational.
⇒7 + 4√3 is irrational.
Hence, (√3 + 2)2 is irrational.
(iii) 
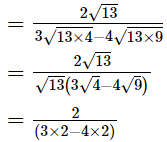
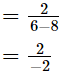
= −1, which is an integer
Hence, 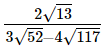 is rational.
is rational.
(iv) √8 + 4√32 −6√2
=2√2 + 4 × 4√2 − 6√2
=2√2 + 16√2 − 6√2
=12√2
Since, the product of a rational number and an irrational number is always an irrational.
Hence, √8 + 4√32 − 6√2 is rational.
Q.7. On her birthday Reema distributed chocolates in an orphanage. The total number of chocolates she distributed is given by (5+ √11) (5− √11).
(i) Find the number of chocolates distributed by her.
(ii) Write the moral values depicted here by Reema.
Ans.
(i) As, (5 + √11) (5 − √11)
=52−(√11)2 [(a+b)(a−b)=a2−b2]
=25 − 11
=14
Hence, the number of chocolates distributed by Reema is 14.
(ii) The moral values depicted here by Reema is helpfulness and caring.
Disclaimer: The moral values may vary from person to person.
Q.8. Simplify
(i) 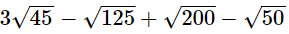
(ii) 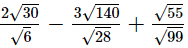
(iii) 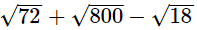
Ans.
(i) 3√45 − √125 + √200 − √50
= 3×3√5 – 5√5 + 10√2 − 5√2
= 9√5 − 5√5 + 5√2
=4√5 + 5√2
(ii) 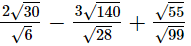
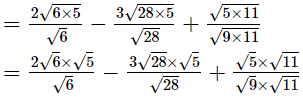
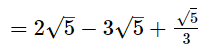

(iii) 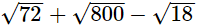
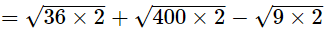
= 6√2 + 20√2 − 3√2
= 23√2
 |
Download the notes
RS Aggarwal Solutions: Number System- 2
|
Download as PDF |
RS Aggarwal Exercise 1.5 Number System
Q.1. Represent √5 on the number line.
Ans.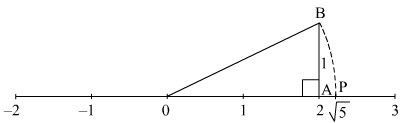
To represent √5 on the number line, follow the following steps of construction:
(i) Mark points 0 and 2 as O and P, respectively.
(ii) At point A, draw AB ⊥ OA such that AB = 1 units.
(iii) Join OB.
(iv) With O as centre and radius OB, draw an arc intersecting the number line at point P.
Thus, point represents √5 on the number line.
Justification:
In right ΔOAB,
Using Pythagoras theorem,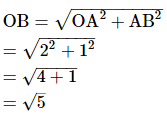
Q.2. Locate √3 on the number line
Ans.
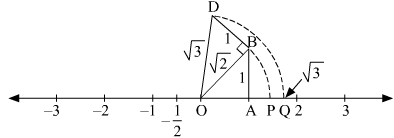
To represent √3 on the number line, follow the following steps of construction:
(i) Mark points 0 and 1 as O and A, respectively.
(ii) At point A, draw AB ⊥ OA such that AB = 1 units.
(iii) Join OB.
(iv) At point B, draw DB ⊥ OA such that DB = 1 units.
(v) Join OD.
(vi) With O as centre and radius OD, draw an arc intersecting the number line at point Q.
Thus, point Q represents √3 on the number line.
Justification:
In right Δ OAB,
Using Pythagoras theorem,
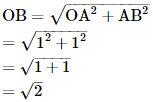
Again, in right ΔODB,
Using Pythagoras theorem,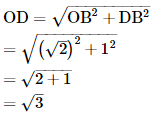
Q.3. Locate √10 on the number line.
Ans.
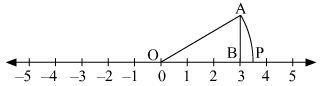
To represent √10 on the number line, follow the following steps of construction:
(i) Mark points 0 and 3 as O and B, respectively.
(ii) At point A, draw AB ⊥ OA such that AB = 1 units.
(iii) Join OA.
(iv) With O as centre and radius OA, draw an arc intersecting the number line at point P.
Thus, point P represents √10 on the number line.
Justification:
In right Δ OAB,
Using Pythagoras theorem,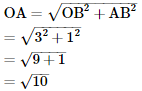
Q.4. Locate √8 on the number line.
Ans.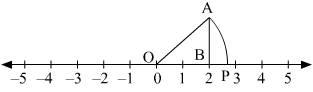
To represent √8 on the number line, follow the following steps of construction:
(i) Mark points 0 and 2 as O and B, respectively.
(ii) At point B, draw AB ⊥ OA such that AB = 2 units.
(iii) Join OA.
(iv) With O as centre and radius OA, draw an arc intersecting the number line at point P.
Thus, point P represents √8 on the number line.
Justification:
In right ΔOAB,
Using Pythagoras theorem,

Q.5. Represent 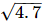 geometrically on the number line.
geometrically on the number line.
Ans.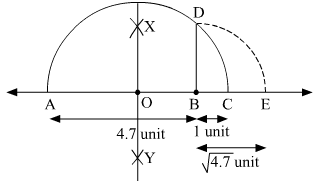
To represent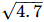 on the number line, follow the following steps of construction:
on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 4.7 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with B as 0, C as 1, and so on, then point E represents 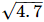 .
.
Justification:
Here, in semi-circle, radii OA = OC = OD = 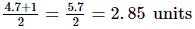
And, OB = AB − AO = 4.7 − 2.85 = 1.85 units
In a right angled triangle OBD,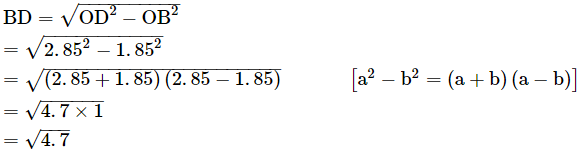
Q.6. Represent 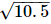 on the number line.
on the number line.
Ans.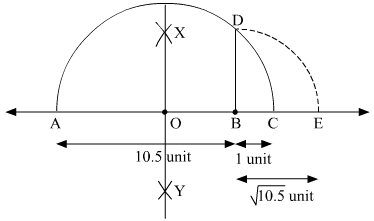
To represent 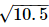 on the number line, follow the following steps of construction:
on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 10.5 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with B as 0, C as 1, and so on, then point E represents 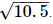
Justification:
Here, in semi-circle, radii OA = OC = OD = 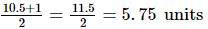
And, OB = AB − AO = 10.5 − 5.75 = 4.75 units
In a right angled triangle OBD,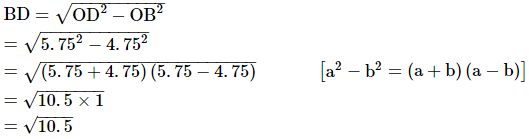
Q.7. Represent 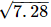 geometrically on the number line.
geometrically on the number line.
Ans.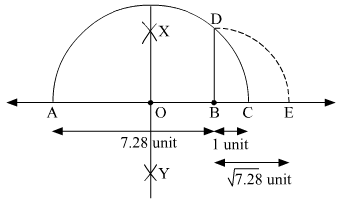
To represent 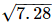 on the number line, follow the following steps of construction:
on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 7.28 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with B as 0, C as 1, and so on, then point E represents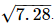
Justification:
Here, in semi-circle, radii OA = OC = OD =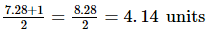
And, OB = AB − AO = 7.28 − 4.14 = 3.14 units
In a right angled triangle OBD,

Q.8. Represent (1 + 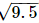 ) on the number line.
) on the number line.
Ans.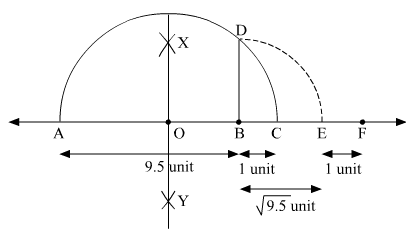
To represent (1 + 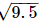 ) on the number line, follow the following steps of construction:
) on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 9.5 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
(vii) From E, mark a point F on the same given line such that EF = 1 unit.
Thus, let us treat the given line as the number line, with B as 0, C as 1, E as 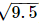 and so on, then point F represents (1+
and so on, then point F represents (1+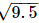 ).
).
Justification:
Here, in semi-circle, radii OA = OC = OD = 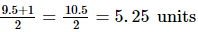
And, OB = AB − AO = 9.5 − 5.25 = 4.25 units
In a right angled triangle OBD,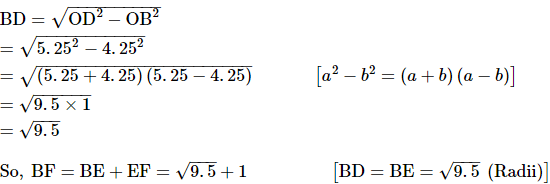
Q.9. Visualize the representation of 3.765 on the number line using successive magnification.
Ans.
3 < 3.765 < 4
Divide the gap between 3 and 4 on the number line into 10 equal parts.
Now, 3.7 < 3.765 < 3.8
In order to locate the point 3.765 on the number line, divide the gap between 3.7 and 3.8
into 10 equal parts.
Further, 3.76 < 3.765 < 3.77
So, to locate the point 3.765 on the number line, again divide the gap between 3.76 and 3.77 into 10 equal parts.
Now, the number 3.765 can be located on the number line. This can be shown as follows: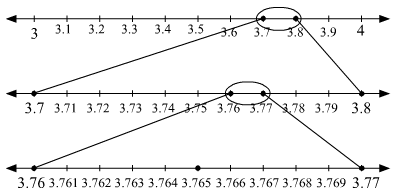
Here, the marked point represents the point 3.765 on the number line.
Q.10. Visualize the representation of 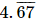 on the number line up to 4 decimal places.
on the number line up to 4 decimal places.
Ans.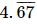 = 4.6767 (Upto 4 decimal places)
= 4.6767 (Upto 4 decimal places)
4 < 4.6767 < 5
Divide the gap between 4 and 5 on the number line into 10 equal parts.
Now, 4.6 < 4.6767 < 4.7
In order to locate the point 4.6767 on the number line, divide the gap between 4.6 and 4.7
into 10 equal parts.
Further, 4.67 < 4.6767 < 4.68
To locate the point 4.6767 on the number line, again divide the gap between 4.67 and 4.68 into 10 equal parts.
Again, 4.676 < 4.6767 < 4.677
To locate the point 4.6767 on the number line, again divide the gap between 4.676 and 4.677 into 10 equal parts.
Now, the number 4.6767 can be located on the number line. This can be shown as follows: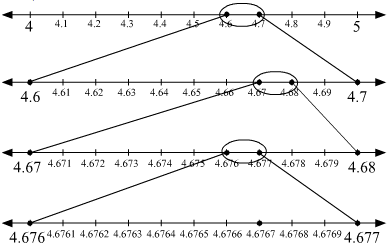
Here, the marked point represents the point 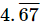 on the number line up to 4 decimal places.
on the number line up to 4 decimal places.
RS Aggarwal Exercise 1.6 Number System
Q.1. Write the rationalising factor of the denominator in 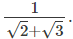
Ans.
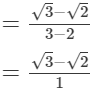
Here, the denominator i.e. 1 is a rational number. Thus, the rationalising factor of the denominator in 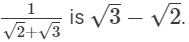 Q.2. Rationalise the denominator of each of the following.
Q.2. Rationalise the denominator of each of the following.
(i)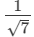
(ii)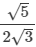
(iii)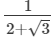
(iv)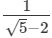
(v)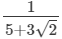
(vi)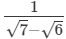
(vii)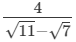
(viii)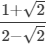
(ix)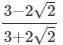
Ans.
(i)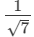 On multiplying the numerator and denominator of the given number by √7, we get:
On multiplying the numerator and denominator of the given number by √7, we get: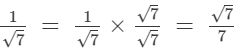 (ii)
(ii)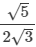
On multiplying the numerator and denominator of the given number by √3, we get: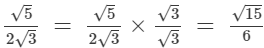 (iii)
(iii)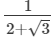
On multiplying the numerator and denominator of the given number by 2 - √3, we get: (iv)
(iv)
On multiplying the numerator and denominator of the given number by √5 +2, we get:
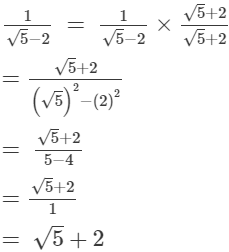 (v)
(v)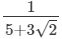
On multiplying the numerator and denominator of the given number by 5-3√2, we get: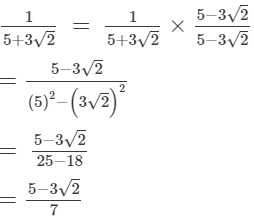 (vi)
(vi)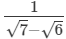
Multiplying the numerator and denominator by √7+√6, we get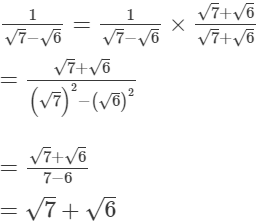 (vii)
(vii)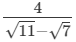
Multiplying the numerator and denominator by √11+√7, we get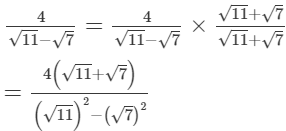
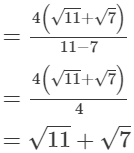 (viii)
(viii)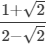
Multiplying the numerator and denominator by 2+√2, we get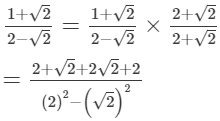
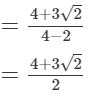 (ix)
(ix)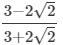
Multiplying the numerator and denominator by 3-2√2, we get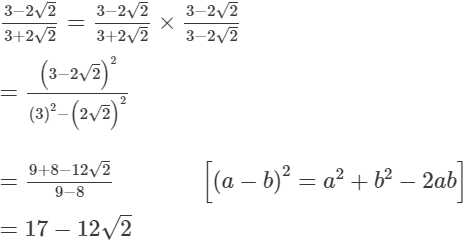
Q.3. It being given that √2 = 1.414, √3 = 1.732, √5 = 2.236 and √10 = 3.162, find the value of three places of decimals, of each of the following.
(i)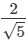
(ii)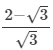
(iii)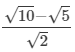
Ans.
(i)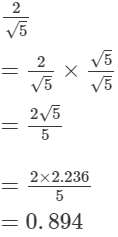
(ii)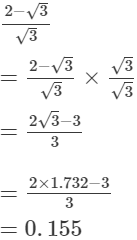
(iii)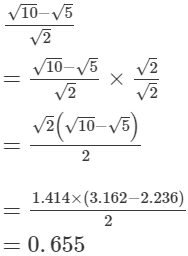
Q.4. Find rational numbers a and b such that
(i)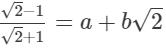
(ii)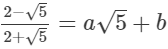
(iii)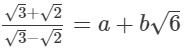
(iv)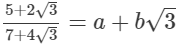
Ans.
(i)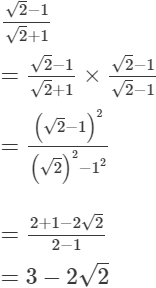

(ii)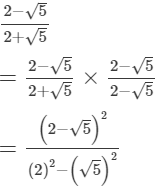
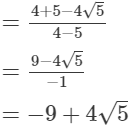
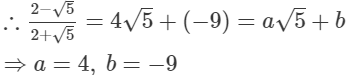 (iii)
(iii)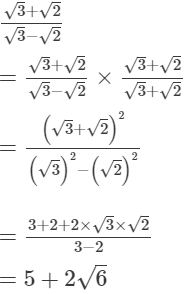
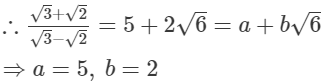
(iv)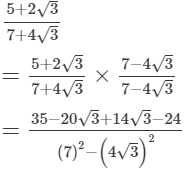
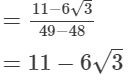
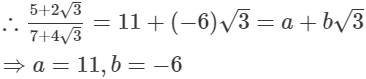
Q.5. It being given that √3 = 1.732, √5 = 2.236, √6 = 2.449 and √10 = 3.162, find to three places of decimal, the value of each of the following.
(i)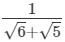
(ii)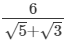
(iii)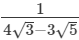
(iv)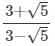
(v)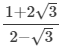
(vi)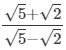
Ans.
(i)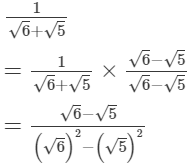
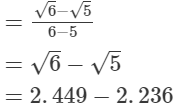
= 0.213
(ii)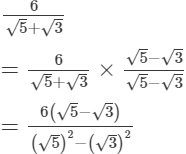
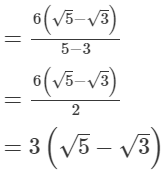
=3 × (2.236 − 1.732)
= 1.512
(iii)
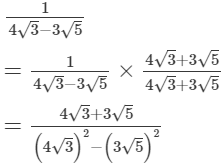
 (iv)
(iv)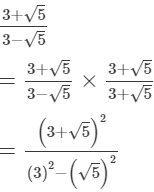
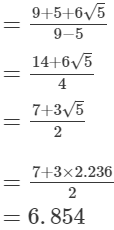
(v)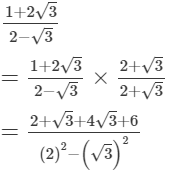
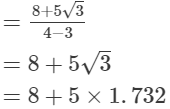
= 16.660
(vi)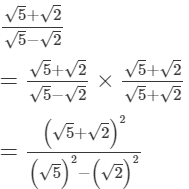
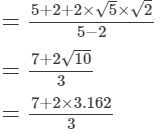
= 4.441
Q.6. Simplify by rationalising the denominator.
(i)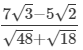
(ii)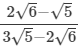
Ans.
(i)
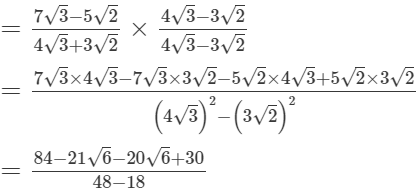
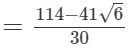 (ii)
(ii)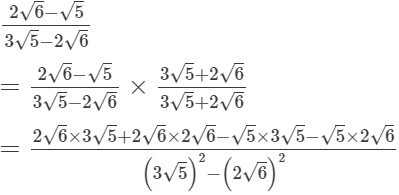
 Q.7. Simplify
Q.7. Simplify
(i)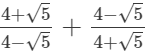
(ii)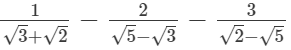
(iii)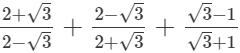
(iv)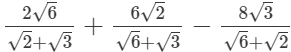
Ans.
(i)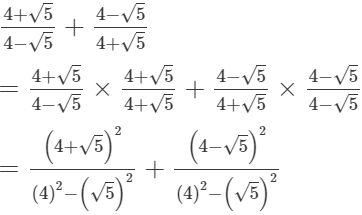
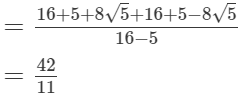 (ii)
(ii)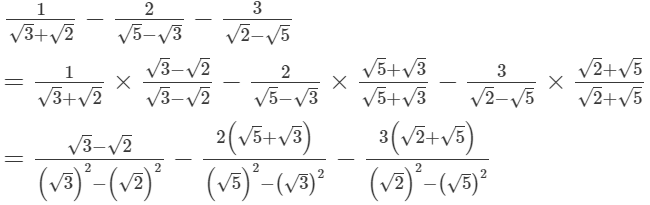
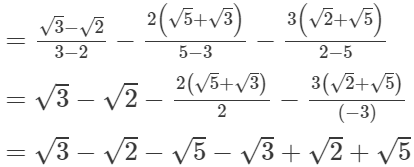 = 0(iii)
= 0(iii)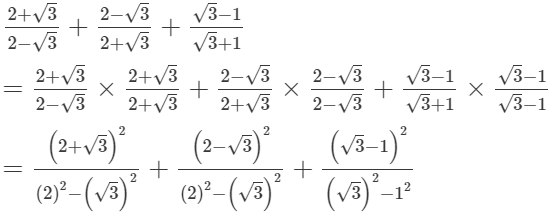
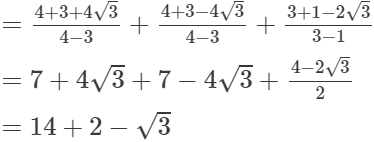
= 16 − √3
(iv)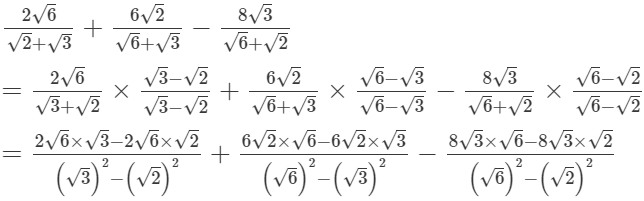
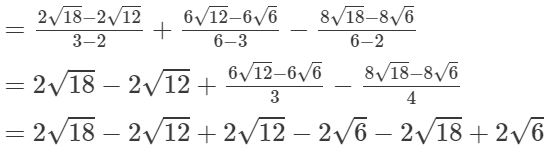
= 0
Q.8. Prove that
(i)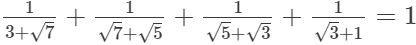
(ii)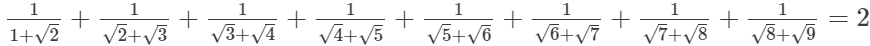
Ans.
(i)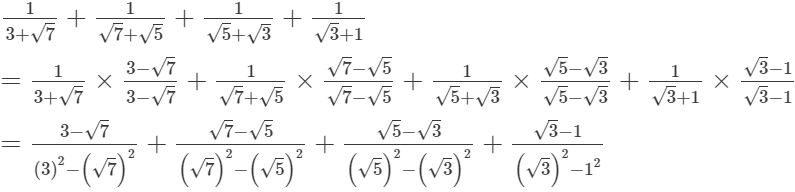
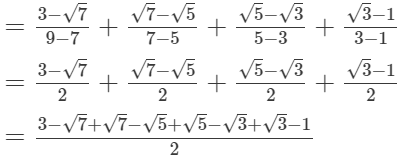
= 2/2
= 1
(ii)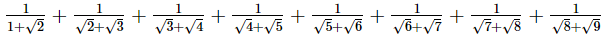
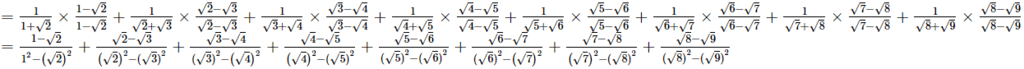
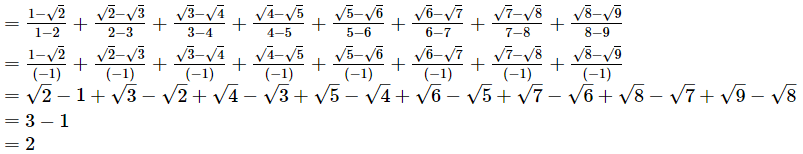 Q.9. Find the values of a and b if
Q.9. Find the values of a and b if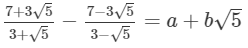
Ans.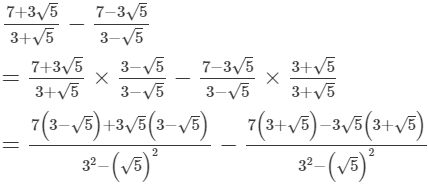

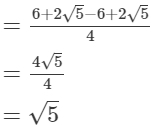
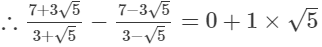
Comparing with the given expression, we get
a = 0 and b = 1
Thus, the values of a and b are 0 and 1, respectively.
Q.10. Simplify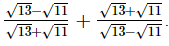 Ans.
Ans.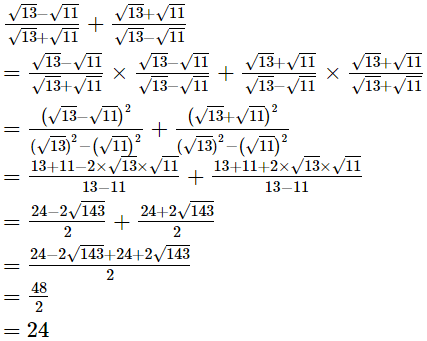
Q.11. If x = 3 + 2√2, check whether 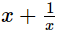 is rational or irrational.Ans.
is rational or irrational.Ans.
x = 3 + 2√2 .....(1)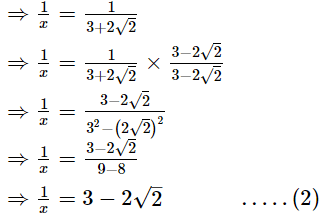 Adding (1) and (2), we get
Adding (1) and (2), we get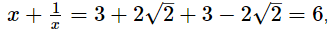 which is a rational numberThus,
which is a rational numberThus, 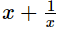 is rational.Q.12.
is rational.Q.12.
If x = 2 − √3, find value of 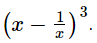
Ans.
x = 2 − √3 .....(1)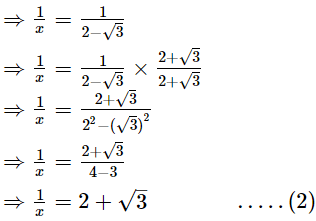 Subtracting (2) from (1), we get
Subtracting (2) from (1), we get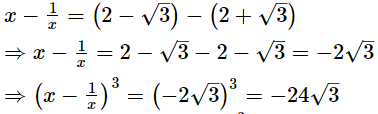 Thus, the value of
Thus, the value of 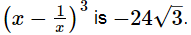 Q.13. If x = 9 − 4√5, find the value of
Q.13. If x = 9 − 4√5, find the value of 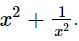
Ans.
x = 9 − 4√5 .....(1)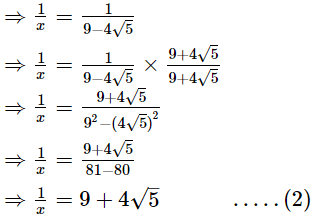 Adding (1) and (2), we get
Adding (1) and (2), we get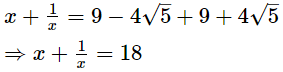 Squaring on both sides, we get
Squaring on both sides, we get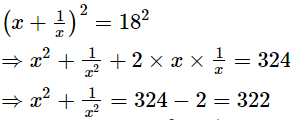 Thus, the value of x2 +
Thus, the value of x2 + 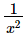 is 322.Q.14. If x =
is 322.Q.14. If x =  find the value of
find the value of 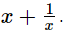 Ans.
Ans.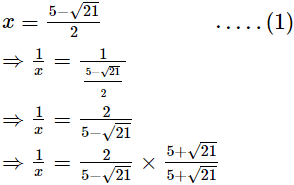
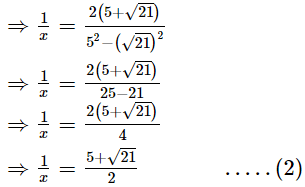
Adding (1) and (2), we get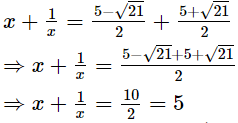 Thus, the value of x +
Thus, the value of x +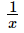 is 5.Q.15. If a = 3 − 2√2, find the value of a2 -
is 5.Q.15. If a = 3 − 2√2, find the value of a2 - 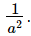
Ans.
a = 3−2√2
⇒ a2 = (3−2√2)2
⇒ a2 = 9 + 8 − 12√2
⇒ a2 = 17 − 12√2 .....(1)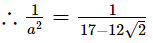
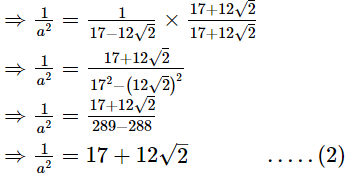 Subtracting (2) from (1), we get
Subtracting (2) from (1), we get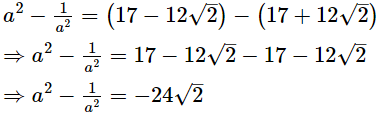 Thus, the value of a2 -
Thus, the value of a2 -  Q.16. If x = √13 + 2√3, find the value of x −
Q.16. If x = √13 + 2√3, find the value of x − 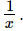
Ans.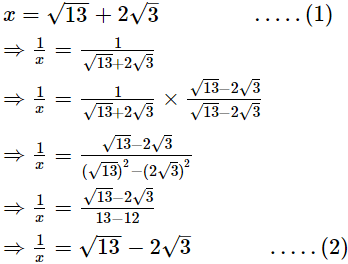
Subtracting (2) from (1), we get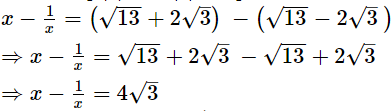 Thus, the value of x
Thus, the value of x 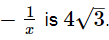 Q.17.
Q.17.
If x = 2 + √3, find the value of 
Ans.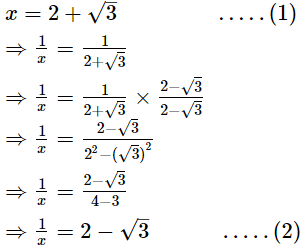
Adding (1) and (2), we get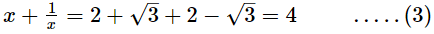 Cubing both sides, we get
Cubing both sides, we get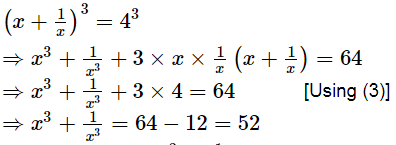 Thus, the value of
Thus, the value of 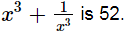 Q.18. If
Q.18. If 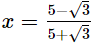 and
and show that
show that 
Ans.
Disclaimer: The question is incorrect.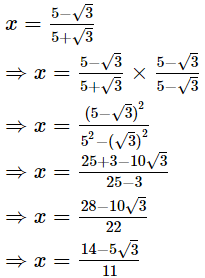
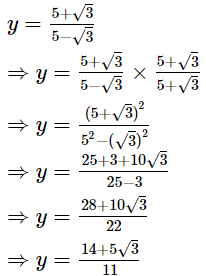
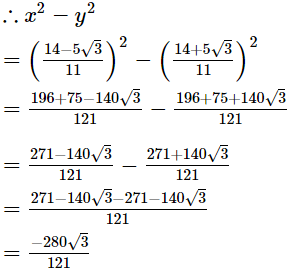 The question is incorrect. Kindly check the question.The question should have been to show that x − y =
The question is incorrect. Kindly check the question.The question should have been to show that x − y = 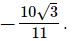
 Q.19. If a =
Q.19. If a = 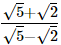 and b =
and b = 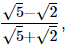 show that 3a2 + 4ab − 3b2 =
show that 3a2 + 4ab − 3b2 = 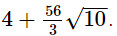
Ans.
According to question,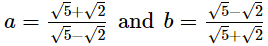
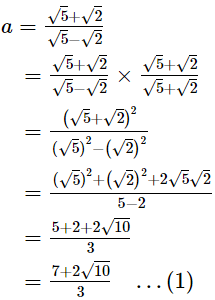
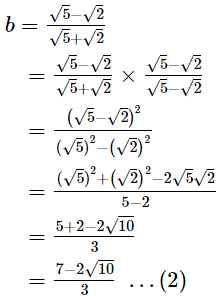 Now,3a2 + 4ab − 3b2
Now,3a2 + 4ab − 3b2
= 3(a2 − b2) + 4ab
= 3 (a + b)(a − b) + 4ab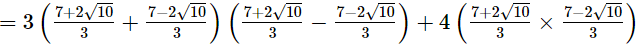
 Hence, 3a2 + 4ab − 3b2 =
Hence, 3a2 + 4ab − 3b2 = 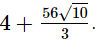 Q.20.
Q.20.
If a = 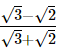 and b =
and b =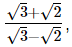 find the value of a2 + b2 – 5ab.
find the value of a2 + b2 – 5ab.
Ans.
According to question,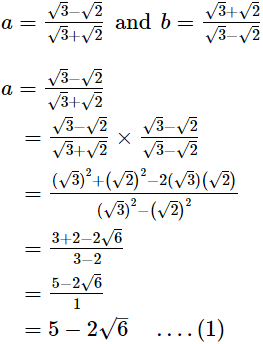
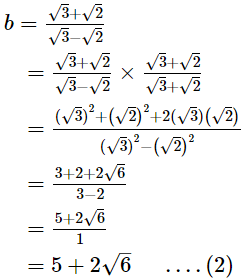 Now,
Now,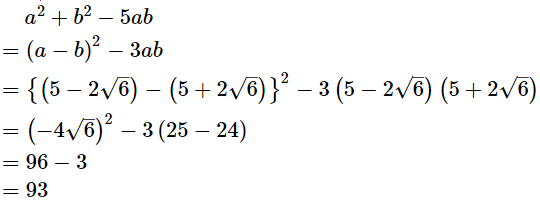 Hence, the value of a2 + b2 – 5ab is 93.
Hence, the value of a2 + b2 – 5ab is 93.
Q.21.
If p =  and q =
and q =  find the value of p2 + q2.
find the value of p2 + q2.
Ans.
According to question,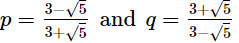
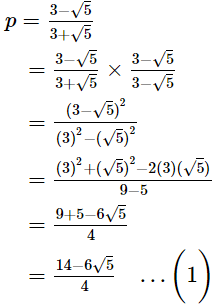
 Now,p2 + q2 = (p+q)2 − 2pq
Now,p2 + q2 = (p+q)2 − 2pq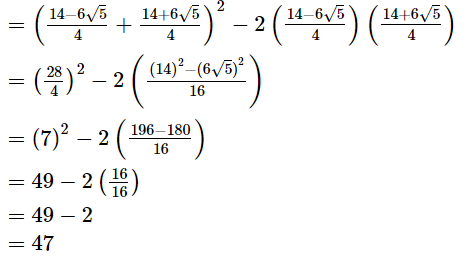 Hence, the value of p2 + q2 is 47.
Hence, the value of p2 + q2 is 47.
Q.22. Rationalise the denominator of each of the following.
(i)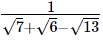
(ii) 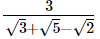
(iii)
Ans.
(i)
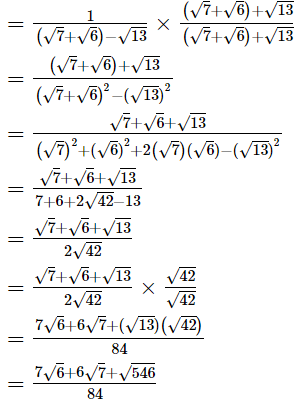 Hence, the rationalised form is
Hence, the rationalised form is 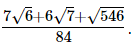 (ii)
(ii) 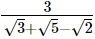
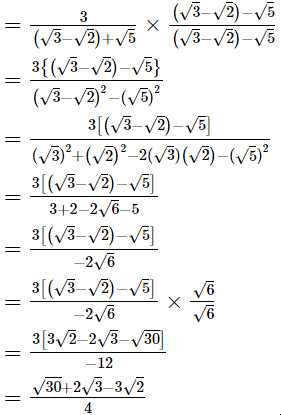
Hence, the rationalised form is 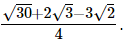 (iii)
(iii) 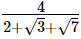
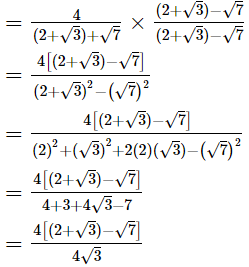
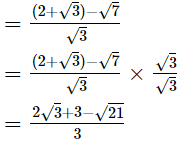
Hence, the rationalised form is 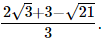 Q.23. Given, √2 = 1.414 and √6 = 2.449, find the value of
Q.23. Given, √2 = 1.414 and √6 = 2.449, find the value of 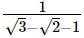 correct to 3 places of decimal.
correct to 3 places of decimal.
Ans.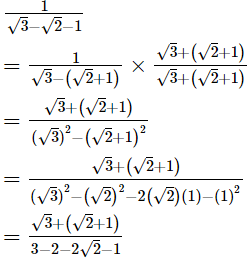
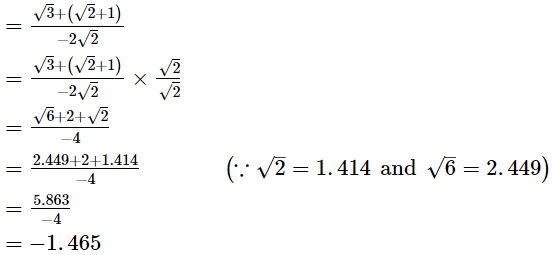
Hence, the value of 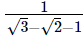 correct to 3 places of decimal is −1.465.Q.24. If x =
correct to 3 places of decimal is −1.465.Q.24. If x =  find the value of x3 – 2x2 – 7x + 5.
find the value of x3 – 2x2 – 7x + 5.
Ans.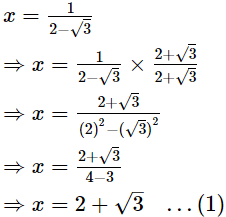
Now,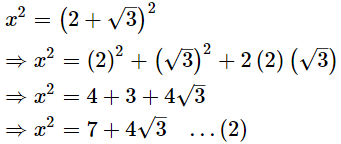
Also,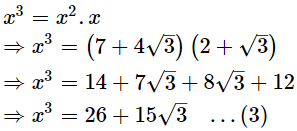
Now,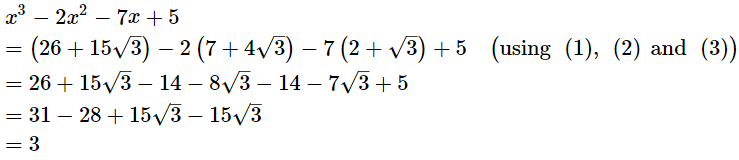 Hence, the value of x3 – 2x2 – 7x + 5 is 3.
Hence, the value of x3 – 2x2 – 7x + 5 is 3.
Q.25. Evaluate 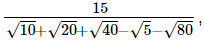 it being given that √5 = 2.236 and √10 = 3.162.Hint
it being given that √5 = 2.236 and √10 = 3.162.Hint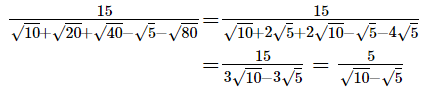 Ans.
Ans.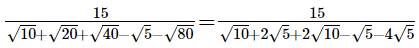
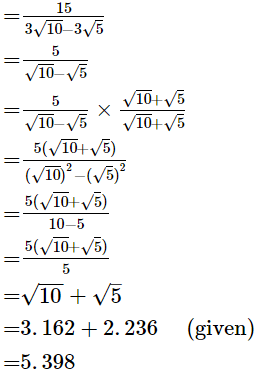
Hence,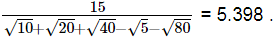
RS Aggarwal Exercise 1.7 Number System
Q.1. Simplify
(i) 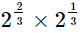
(ii) 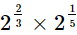
(iii) 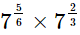
(iv) 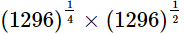
Ans.
(i) 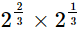
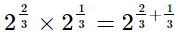
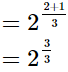 =21
=21
= 2
(ii) 
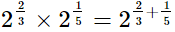
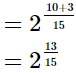
(iii)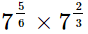
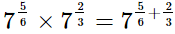
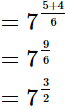
(iv) 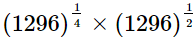
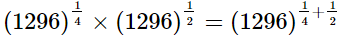
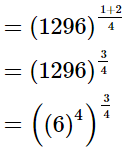
= (6)3
= 216
Q.2. Simplify:
(i)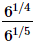
(ii)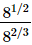
(iii)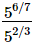
Ans.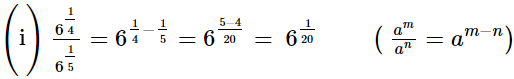

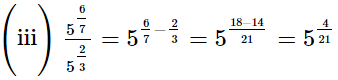
Q.3. Simplify:
(i) 31/4 × 51/4
(ii) 25/8 × 35/8
(iii) 61/2 × 71/2
Ans.
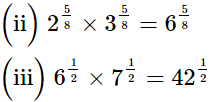
Q.4. Simplify:
(i) (34)1/4
(ii) (31/3)4
(iii) 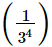
Ans.
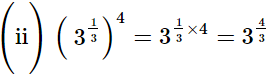
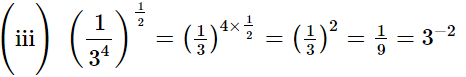
Q.5. Evaluate
(i)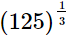
(ii)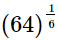
(iii)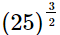
(iv)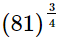
(v)
(vi)
Ans.
(i) 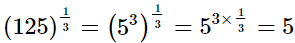
(ii)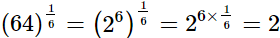
(iii)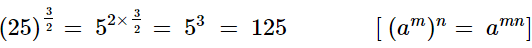
(iv)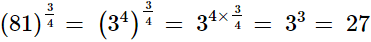
(v)
(vi)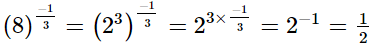
Q.6. If a = 2, b = 3, find the values of
(i) (ab + ba)–1
(ii) (aa + bb)–1
Ans.
(i) (ab + ba)–1
(ab + ba) −1 = (23 + 32) −1
= (8 + 9)−1
= (17)−1
= 1/17
(ii) (aa + bb)–1
(aa + bb)−1 = (22 + 33)−1
= (4 + 27)−1
= (31)−1
=1/31
Q.7. Simplify
(i)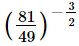
(ii) (14641)0.25
(iii)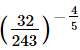
(iv)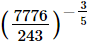 Ans.
Ans.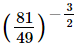
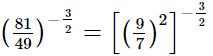
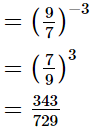
(ii) (14641)0.25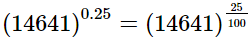
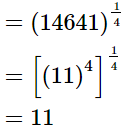
(iii) 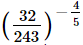
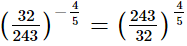
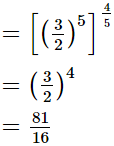
(iv)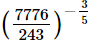
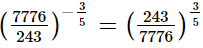
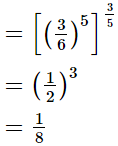
Q.8. Evaluate
(i) 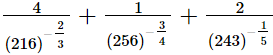
(ii) 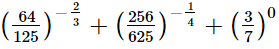
(iii) 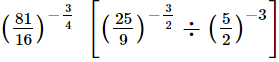
(iv) 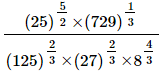
Ans.
(i)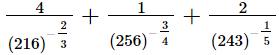
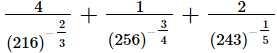
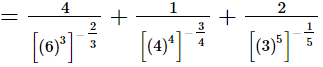
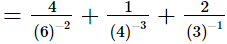
=4(6)2 + (4)3 + 2(3)
=144 + 64 + 6
=214
(ii) 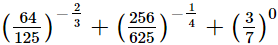
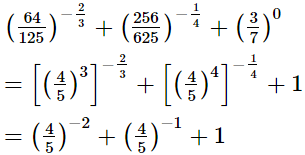
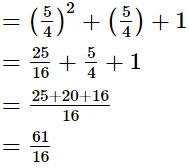 (iii)
(iii) 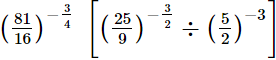
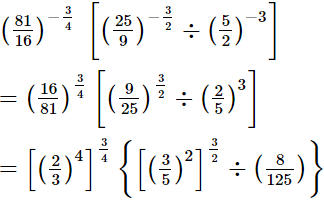
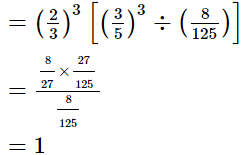
(iv) 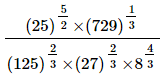
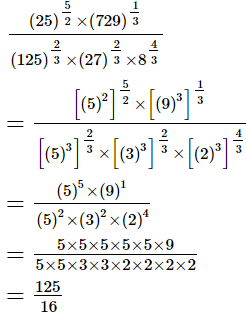
Q.9. Evaluate
(i)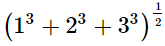
(ii)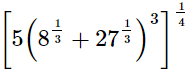
(iii) 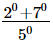
(iv) 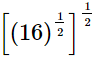
Ans.
(i) 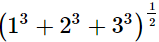
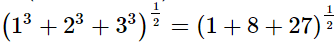
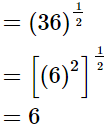
(ii) 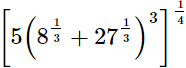
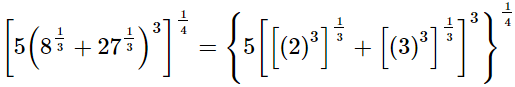
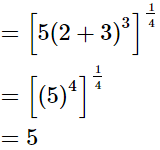
(iii) 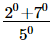
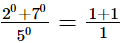
= 2
(iv) 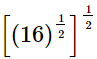
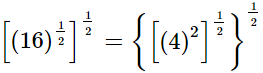
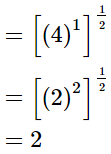
Q.10. Prove that
(i) 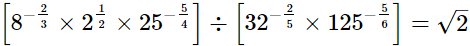
(ii) 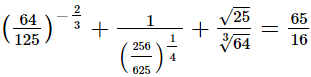
(iii) 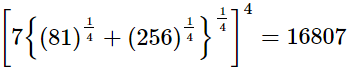
Ans.
(i) 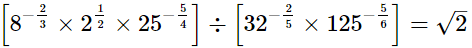
LHS = 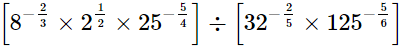
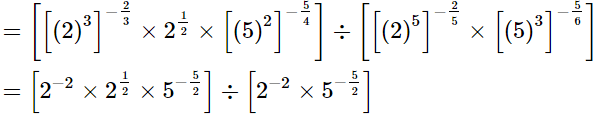
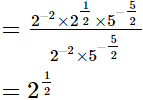
= √2
= RHS
∴ 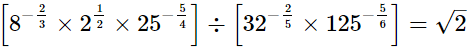 (ii)
(ii) 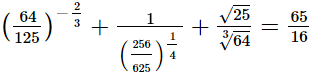
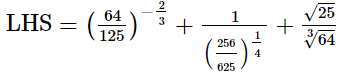
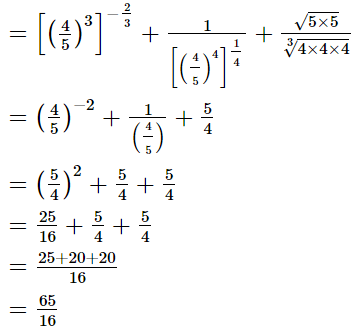 = RHS∴
= RHS∴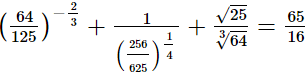 (iii)
(iii) 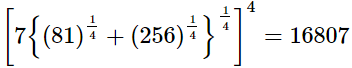
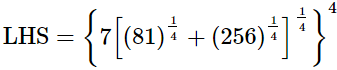
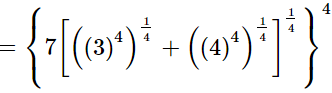
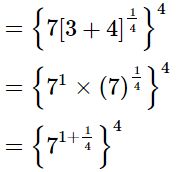
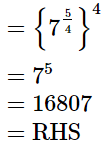
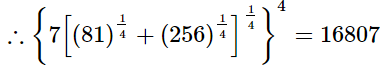
Q.11. Simplify 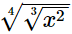 and express the result in the exponential form of x.
and express the result in the exponential form of x.
Ans.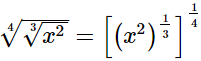
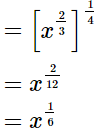
Hence, the result in the exponential form is 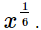 Q.12. Simplify the product
Q.12. Simplify the product 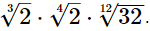
Ans.

Q.13. Simplify
(i) 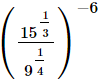
(ii)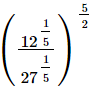
(iii)
Ans.
(i) 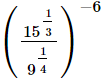
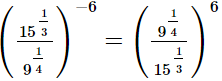
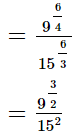
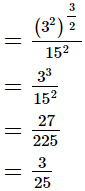
(ii)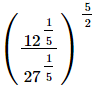
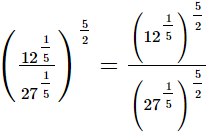
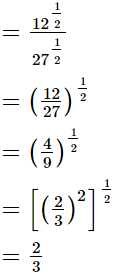
(iii)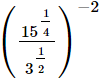
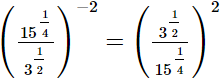
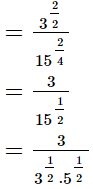
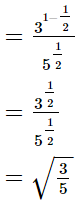
Q.14. Find the value of x in each of the following.
(i)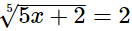
(ii)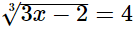
(iii)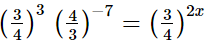
(iv)5x−3 × 32x−8 = 225
(v)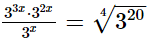 Ans.
Ans.
(i) 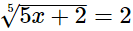
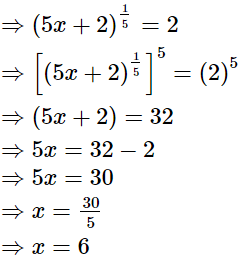
Hence, the value of x is 6.
(ii) 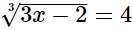
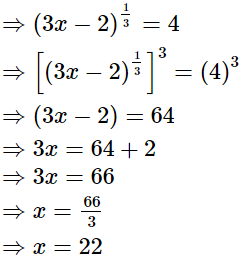
Hence, the value of x is 22.
(iii) 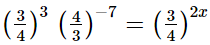
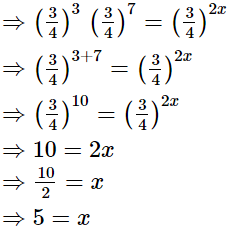
Hence, the value of x is 5.
(iv) 5x−3×32x−8 = 225
⇒5x−3 × 32x−8 = (15)2
⇒5x−3 × 32x − 8 = 52 × 32
⇒x − 3 = 2 and 2x − 8 = 2
⇒x = 2 + 3 and 2x = 2 + 8
⇒x = 5 and 2x = 10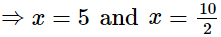 ⇒ x = 5 and x = 5⇒ x = 5
⇒ x = 5 and x = 5⇒ x = 5
Hence, the value of x is 5.
(v)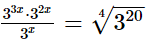
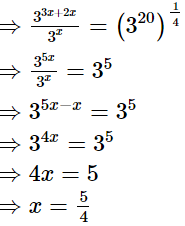
Hence, the value of x is 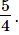 Q.15.
Q.15.
Prove that
(i)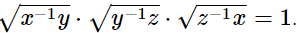
(ii)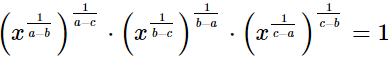
(iii)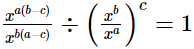
(iv)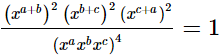
Ans.
(i) 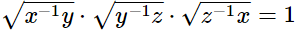
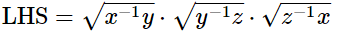
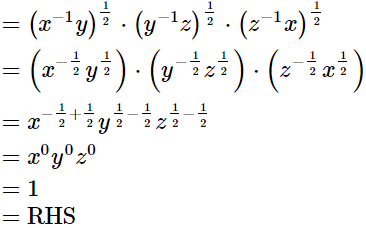
Hence, 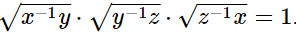
(ii)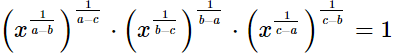
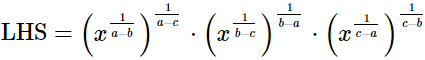
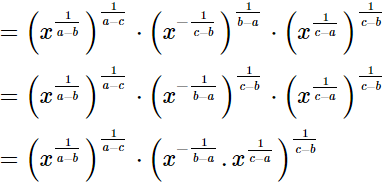
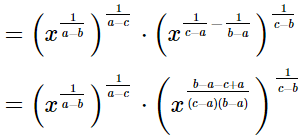
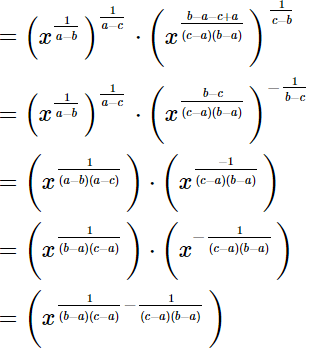
=x0
=1
= RHS
Hence,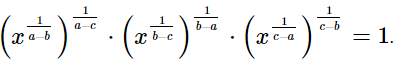 (iii)
(iii)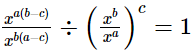
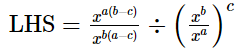
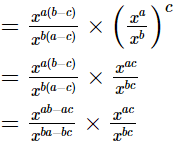
=xab−ac−ba+bc.xac−bc
=x−ac+bc.xac−bc
=x−ac+bc+ac−bc
=x0
= 1
= RHS
Hence, 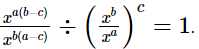 (iv)
(iv) 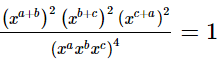
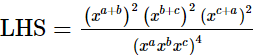
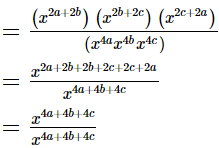
= 1
= RHS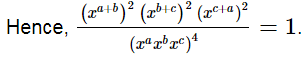
Q.16. If x is a positive real number and exponents are rational numbers, simplify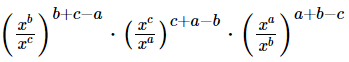
Ans.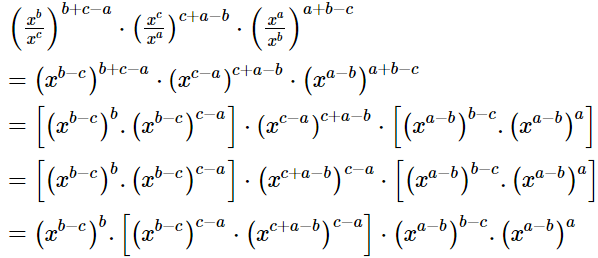
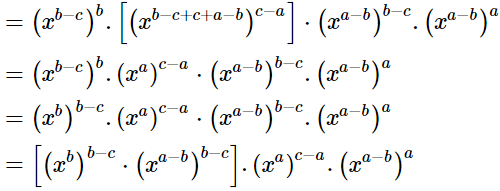
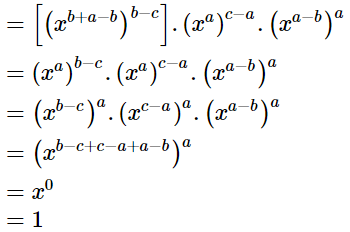
Q.17. If 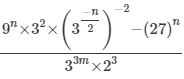 = 1/27, prove that m – n = 1.
= 1/27, prove that m – n = 1.
Ans.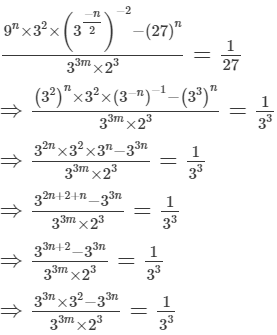
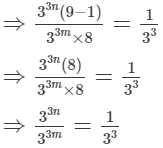
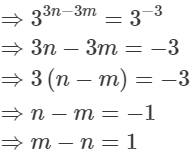 Hence, m - n = 1
Hence, m - n = 1
Q.18. Write the following in ascending order of magnitude.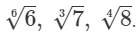
Ans.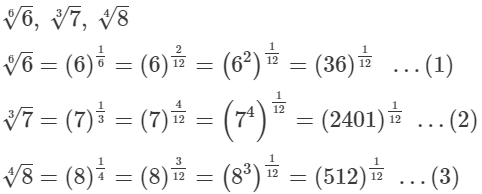
On Comparing (1), (2) and (3), we get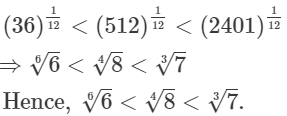
|
45 videos|412 docs|53 tests
|
FAQs on RS Aggarwal Solutions: Number System- 2 - Mathematics (Maths) Class 9
| 1. What are the different exercises covered in RS Aggarwal's Number System book? |  |
| 2. What topics are covered in Exercise 1.2 of RS Aggarwal's Number System book? |  |
| 3. How does Exercise 1.4 of RS Aggarwal's Number System book contribute to learning? |  |
| 4. What is the significance of Exercise 1.5 in RS Aggarwal's Number System book? |  |
| 5. Are there any solutions available for the exercises in RS Aggarwal's Number System book? |  |

































