RS Aggarwal Solutions: Number System- 3 | Extra Documents & Tests for Class 9 PDF Download
Q.1. What are irrationl numbers? How do they differ from rational numbers? Give examples.
Ans. A number that can neither be expressed as a terminating decimal nor be expressed as a repeating decimal is called an irrational number. A rational number, on the other hand, is always a terminating decimal, and if not, it is a repeating decimal.
Examples of irrational numbers:
0.101001000...
0.232332333...
Q.2. Classify the following numbers as rational or irrational. give reasons to support your answer.
(i) 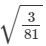
(ii)
(iii)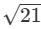
(iv)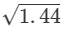
(v)
(vi) 4.1276
(vii) 22/7
(viii) 1.232332333..
(ix) 3.040040004....
(x) 2.356565656...
(xi) 6.834834...
Ans. 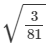
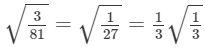
It is an irrational number.
(ii) = 19
= 19
So, it is rational.
(iii)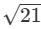
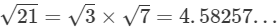
It is an irrational number.
(iv)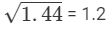
So, it is rational.
(v) 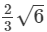
It is an irrational number
(vi) 4.1276
It is a terminating decimal. Hence, it is rational.
(vii) 22/7
22/7 is a rational number because it can be expressed in the p/q form.
(viii) 1.232332333...is an irrational number because it is a non−terminating, non−repeating decimal.
(ix) 3.040040004... is an irrational number because it is a non−terminating, non−repeating decimal.
(x) 2.356565656... is a rational number because it is repeating.
(xi) 6.834834... is a rational number because it is repeating.
Q.3. Let x be a rational number and y be an irrational number. Is x + y necessarily an irrational number? Give a example in support of your answer.
Ans.
x be a rational number and y be an irrational number then x + y necessarily will be an irrational number.
Example: 5 is a rational number but √2 is irrational.
So, 5 + √2 will be an irrational number.
Q.4. Let a be a rational number and b be an irrational number. Is ab necessarily an irrational number? Justify your answer with an example.
Ans. a be a rational number and b be an irrational number then ab necessarily will be an irrational number.
Example: 6 is a rational number but √5 is irrational. And 6√5 is also an irrational number.
Q.5. Is the product of two irrationals always irrational? Justify your answer.
Ans. Product of two irrational numbers is not always an irrational number.
Example: √5 is irrational number. And √5 × √5 = 5 is a rational number. But the product of another two irrational numbers √2 and √3 is √6 which is also an irrational numbers.
Q.6. Give an example of two irrational numbers whose
(i) difference is an irrational number.
(ii) difference is a rational number.
(iii) sum is an irrational number.
(iv) sum is a rational number.
(v) product is an irrational number.
(vi) product is a rational number.
(vii) quotient is an irrational number.
(viii) quotient is a rational number.
Ans.
(i) 2 irrational numbers with difference an irrational number will be 3−√5 and 3+√5.
(ii) 2 irrational numbers with difference is a rational number will be 5+√3 and 2+√3
(iii) 2 irrational numbers with sum an irrational number 7+√5 and √6 − 8
(iv) 2 irrational numbers with sum a rational number is 3−√2 and 3 + √2
(v) 2 irrational numbers with product an irrational number will be 6 + √3 and 7−√3
(vi) 2 irrational numbers with product a rational number will be (5 + √7) and (5 − √7)
(vii) 2 irrational numbers with quotient an irrational number will be √15 and √5
(viii) 2 irrational numbers with quotient a rational number will be √63 and √7.
Question 7: Examine whether the following numbers are rational or irrational.
(i) 3 + √3
(ii) √7 − 2
(iii)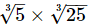
(iv) 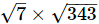
(v) 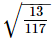
(vi) √8 × √2
Ans. (i) Let us assume, to the contrary, that 3 + √3 is rational.
Then, 3+√3 = pq, where p and q are coprime and q ≠ 0.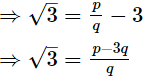
Since, p and q are are integers.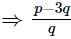 is rational.
is rational.
So, √3 is also rational.
But this contradicts the fact that √3 is irrational.
This contradiction has arisen because of our incorrect assumption that 3 + √3 is rational.
Hence, 3 + √3 is irrational.
(ii) Let us assume, to the contrary, that √7−2 is rational.
Then, √7 − 2 = p/q, where p and q are coprime and q ≠ 0.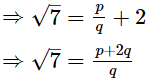
Since, p and q are are integers. is rational.
is rational.
So, √7 is also rational.
But this contradicts the fact that √7 is irrational.
This contradiction has arisen because of our incorrect assumption that √7 − 2 is rational.
Hence, √7 − 2 is irrational.
(iii) As,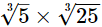
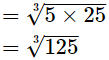
= 5, which is an integer
Hence, 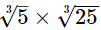 is rational.
is rational.
(iv) As, 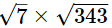
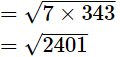
= 49, which is an integer
Hence, 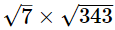 is rational.
is rational.
(v) As,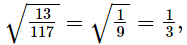 which is rational
which is rational
Hence, 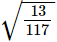 is rational.
is rational.
(vi) As, √8 × √2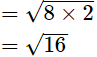
= 4, which is an integer
Hence, √8 × √2 is rational.
Q.8. Insert a rational and an irrational number between 2 and 2.5.
Ans. As, few rational numbers between 2 and 2.5 are: 2.1, 2.2, 2.3, 2.4, ...
And,
Since, 2 = √4 and 2.5= 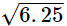
So, irrational number between 2 ans 2.5 are: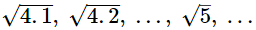
Hence, a rational and an irrational number can be 2.1 and √5, respectively.
Disclaimer: There are infinite rational and irrational numbers between any two rational numbers.
Q.9. How many irrational numbers lie between √2 and √3? Find any three irrational numbers lying between √2 and √3.
Ans. There are infinite number of irrational numbers lying between √2 and √3.
As, √2 = 1.414 and √3 = 1.732
So, the three irrational numbers lying between √2 and √3 are:
1.420420042000..., 1.505005000... and 1.616116111...
Q.10. Find two rational and two irrational number between 0.5 and 0.55.
Ans. The two rational numbers between 0.5 and 0.55 are: 0.51 and 0.52
The two irrational numbers between 0.5 and 0.55 are: 0.505005000... and
0.5101100111000...
Disclaimer: There are infinite number of rational and irrational numbers between 0.5 and 0.55.
Q.11. Find three different irrational numbers between the rational numbers 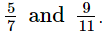
Ans. As, 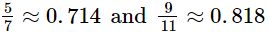
So, the three different irrational numbers are: 0.72020020002..., 0.7515511555111... and 0.808008000...
Disclaimer: There are an infinite number of irrational numbers between two rational numbers.
Q.12. Find two rational numbers of the form p/q between the numbers 0.2121121112... and 0.2020020002... .
Ans. The rational numbers between the numbers 0.2121121112... and 0.2020020002... are:
Disclaimer: There are an infinite number of rational numbers between two irrational numbers.
Q.13. Find two irrational numbers between 0.16 and 0.17.
Ans. The two irrational numbers between 0.16 and 0.17 are 0.161161116... and 0.1606006000...
Disclaimer: There are an infinite number of irrational numbers between two rational numbers.
Q.14. State in each case, whether the given statement is true of false.
(i) The sum of two rational numbers is rational.
(ii) The sum of two irrational numbers is irrational.
(iii) The product of two rational numbers is rational.
(iv) The product of two irrational number is irrational.
(v) The sum of a rational number and an irrational number is irrational.
(vi) The product of a nonzero rational number and an irrational number is a rational number.
(vii) Every real number is rational.
(viii) Every real number is either rational or irrational.
(ix) π is irrational and 22/7 is rational.
Ans.
(i) True
(ii) False
Example: (2 + √3) + (2 − √3) = 4
Here, 4 is a rational number.
(iii) True
(iv) False
Example: √ 3× √3=3
Here, 3 is a rational number.
(v) True
(vi) False
Example: (4)×√5 = 4√5
Here, 4√5 is an irrational number.
(vii) False
Real numbers can be divided into rational and irrational numbers.
(viii) True
(ix) True
|
1 videos|228 docs|21 tests
|






















