ICAI Notes- Ratio and Proportion, Indices, Logarithms- 2 - CA Foundation PDF Download
1.3 INDICES
LEARNING OBJECTIVES
After reading this unit, a student will learn –
- A meaning of indices and their application;
- Laws of indices which facilitates their easy applications.
We are aware of certain operations of addition and multiplication and now we take up certain higher order operations with powers and roots under the respective heads of indices.
We know that the result of a repeated addition can be held by multiplication e.g.
4 + 4 + 4 + 4 + 4 = 5(4) = 20
a + a + a + a + a = 5(a) = 5a
Now, 4 × 4 × 4 × 4 × 4 = 45;
a × a × a × a × a = a5.
It may be noticed that in the first case 4 is multiplied 5 times and in the second case ‘a’ is multiplied 5 times. In all such cases a factor which multiplies is called the “base” and the number of times it is multiplied is called the “power” or the “index”. Therefore, “4” and “a” are the bases and “5” is the index for both. Any base raised to the power zero is defined to be 1; i.e. ao = 1. We also define 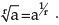
If n is a positive integer, and ‘a’ is a real number, i.e. n ∈ N and a ∈ R (where N is the set of positive integers and R is the set of real numbers), ‘a’ is used to denote the continued product of n factors each equal to ‘a’ as shown below:
an = a × a × a ………….. to n factors.
Here an is a power of “a“ whose base is “a“ and the index or power is “n“.
For example, in 3 × 3 × 3 × 3 = 34 , 3 is base and 4 is index or power.
Law 1
am × an = am+n , when m and n are positive integers; by the above definition, am = a × a ………….. to m factors and an = a × a ………….. to n factors.
∴am × an = (a × a ………….. to m factors) (a × a ……….. to n factors) = a × a ………….. to (m + n) factors
= am+n
Now, we extend this logic to negative integers and fractions. First let us consider this for negative integer, that is m will be replaced by –n. By the definition of am × an = am+n ,
We get a–n×an = a–n+n = a0 = 1
For example 34 × 35 = (3 × 3 × 3 × 3) × (3 × 3 × 3 × 3 × 3) = 34 + 5 = 39
Again, 3–5 = 1/35 = 1/(3 × 3 × 3 × 3 × 3) = 1/243
Example 1: Simplify 2x1/2 3x-1 if x = 4
Solution: We have 2x1/2 3x-1
= 6x1/2 x-1 = 6x1/2-1
= 6x −1/2

Example 2: Simplify 6ab2c3 × 4b–2c–3d
Solution: 6ab2c3 × 4b–2c–3d
= 24 × a × b2 × b–2 × c3 × c–3 d
= 24 × a × b2+(–2) × c3+(–3) × d
= 24 × a × b2–2 × c3–3 × d
= 24 a b0 × c0 × d
= 24ad
Law 2
am/an = am–n, when m and n are positive integers and m > n.
By definition, am = a × a ………….. to m factors
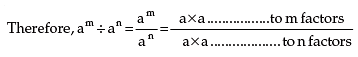
= a × a ……… to m–n factors
= am–n
Now we take a numerical and check the validity of this Law

= 2 × 2 × 2 ……….. to (7–4) factors.
= 2 × 2 × 2 ……….. to 3 factors
= 23 = 8
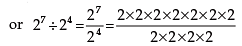
= 2 × 2 × 2 = 21+1+1 = 23
= 8
Example 3: Find the value of 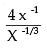
Solution: 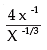
= 4x -1 - (-1 / 3)
= 4x-1 + 1/3

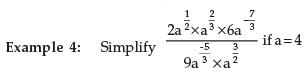
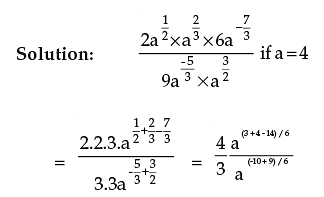
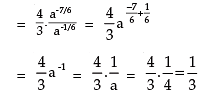
Law 3
(am)n = amn. where m and n are positive integers
By definition (am)n = am × am × am ……….. to n factors
= (a × a ……….. to m factors)………. to n times
= a × a …………. to mn factors
= amn
Following above, (am)n = (am)p/q
(We will keep m as it is and replace n by p/q, where p and q are positive integers)
Now the qth power of (am)p/q is{(am)p/q}q
= (am)(p/q)x q
= amp
If we take the qth root of the above we obtain
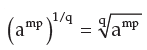
Now with the help of a numerical let us verify this law.
(24)3 = 24 × 24 × 24
= 24+4+4
= 212 = 4096
Law 4
(ab)n = an.bn when n can take all of the values.
For example 63 = (2 × 3) 3 = 2 × 2 × 2 × 3 × 3 × 3 = 23 × 33
First, we look at n when it is a positive integer. Then by the definition, we have
(ab)n = ab × ab ……………. to n factors
= (a × a ……..……. to n factors) (b × b …………. n factors)
= an × bn
When n is a positive fraction, we will replace n by p/q.
Then we will have (ab)n = (ab)p/q
The qth power of (ab)p/q = {(ab)(p/q)}q = (ab)p
Example 5: Simplify (xa.y–b)3 . (x3 y2)–a
Solution: (xa.y–b)3 . (x3 y2)–a
= (xa)3 . (y–b)3 . (x3)–a . (y2)–a
= x3a–3a . y–3b–2a.
= x0. y–3b–2a.
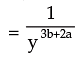
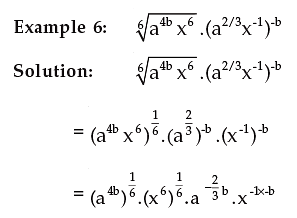

Example 7: 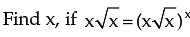
Solution: x (x)1/2 = xx .x x/2
or, x1+ 1/2 = xx + x/2
or, x3/2 = x3x/2
[If base is equal, then power is also equal]

Example 8: Find the value of k from (√9)–7 × (√3)–5 = 3k
Solution: (√9)–7 × (√3)–5 = 3k
or, (32 × 1/2) –7 × (3½) –5 = 3k
or, 3−7−5/2 = 3k
or, 3 –19/2 = 3k or, k = –19/2
1.3.1 LAWS OF INDICES
(i) am × an = am+n (base must be same)
Ex. 23 × 22 = 23+2 = 25
(ii) am ÷ an = am–n
Ex. 25 ÷ 23 = 25–3 = 22
(iii) (am)n = amn
Ex. (25)2 = 25×2 = 210
(iv) ao = 1
Example : 20 = 1, 30 = 1
(v) a–m = 1/am and 1/a–m = am
Example: 2–3 = 1/23 and 1/2–5 = 25
(vi) If ax = ay, then x=y
(vii) If xa = ya, then x=y

1.4 LOGARITHM
LEARNING OBJECTIVE
After reading this unit, a student will get fundamental knowledge of logarithm and its application for solving business problems.
The logarithm of a number to a given base is the index or the power to which the base must be raised to produce the number, i.e. to make it equal to the given number. If there are three quantities indicated by say a, x and n, they are related as follows:
If ax = n
Then x is said to be the logarithm of the number n to the base ‘a’ symbolically it can be expressed as follows:
logan = x
i.e. the logarithm of n to the base ‘a’ is x, we give some illustrations below:
(i) 24 = 16 ⇒ log216 = 4
i.e. the logarithm of 16 to the base 2 is equal to 4
(ii) 103 = 1000 ⇒ log101000 = 3
i.e. the logarithm of 1000 to the base 10 is 3
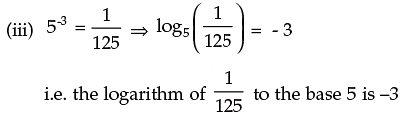
(iv) 23 = 8 ⇒ log28 = 3 i.e. the logarithm of 8 to the base 2 is 3
1. Two equations ax = n
and x = logan are only transformations of each other and should be remembered to change one form of the relation into the other.
2. The logarithm of 1 to any base is zero. This is because any number raised to the power zero is one.
Since a0 = 1 , loga1 = 0
3. The logarithm of any quantity to the same base is unity. This is because any quantity raised to the power 1 is that quantity only.
Since a1 = a , logaa = 1
Illustrations:
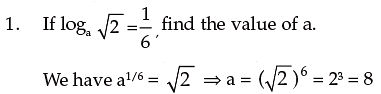
2 . Find the logarithm of 5832 to the base 3√ 2.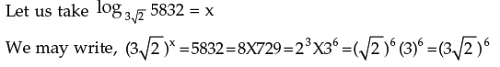
Hence, x = 6
Logarithms of numbers to the base 10 are known as common logarithm.
1.4.1 FUNDAMENTAL LAWS OF LOGARITHM
Logarithm of the product of two numbers is equal to the sum of the logarithms of the numbers to the same base, i.e.
Logamn = logam + logan
Proof:
Let logam = x so that ax = m – (I)
Logan = y so that ay = n – (II)
Multiplying (I) and (II), we get m × n = ax × ay = ax+y
logamn = x + y (by definition)
∴ logamn = logam + logan
2 . The logarithm of the quotient of two numbers is equal to the difference of their logarithms to the same base, i.e.
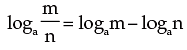
Proof:
Let logam = x so that ax = m ————(I)
logan = y so that ay = n ———————(II)
Dividing (I) by (II) we get
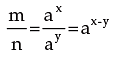
Then by the definition of logarithm, we get
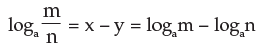
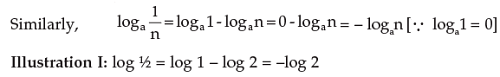
3. Logarithm of the number raised to the power is equal to the index of the power multiplied by the logarithm of the number to the same base i.e.
logamn = n logam
Proof:
Let logam = x so that ax = m
Raising the power n on both sides we get
(ax)n = (m)n
axn = mn (by definition)
logamn = nx
i.e. logamn = n logam
Illustrations II: 1(a) Find the logarithm of 1728 to the base 2√3
Solution: We have 1728 = 26 × 33 = 26 × (√3)6 = (2√3)6; and so, we may write
log 2√3 1728 = 6
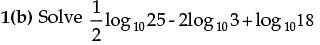
Solution: The given expression
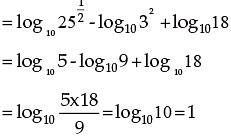
1.4.2 CHANGE OF BASE
If the logarithm of a number to any base is given, then the logarithm of the same number to any other base can be determined from the following relation
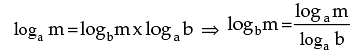
Proof:
Let logam = x, logbm = y and logab = z
Then by definition,
ax = m, by = m and az = b
Also ax = by = (az)y = ayz Therefore, x = yz
⇒ logam = logbm x logab

Putting m = a, we have
logaa = logba x logab
⇒ logba x logab = 1, since logaa = 1.
Example 1: Change the base of log531 into the common logarithmic base.
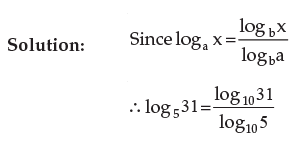
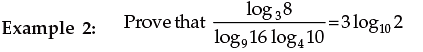
Solution: Change all the logarithms on L.H.S. to the base 10 by using the formula.
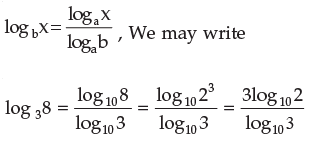
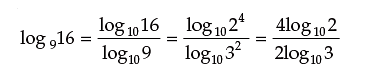
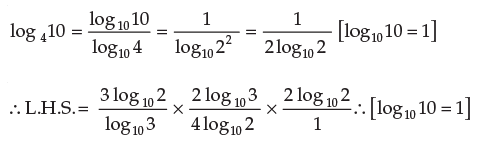
= 3 log102 = R.H.S.
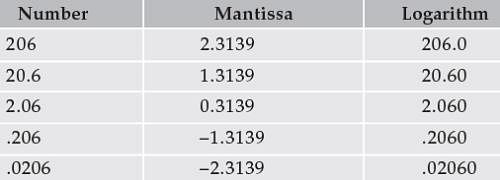
Logarithm Tables:
The logarithm of a number consists of two parts, the whole part or the integral part is called the characteristic and the decimal part is called the mantissa where the former can be known by mere inspection, the latter has to be obtained from the logarithm tables
Characteristic:
The characteristic of the logarithm of any number greater than 1 is positive and is one less than the number of digits to the left of the decimal point in the given number. The characteristic of the logarithm of any number less than one (1) is negative and numerically one more than the number of zeros to the right of the decimal point. If there is no zero then obviously it will be –1. The following table will illustrate it.


Zero on positive characteristic when the number under consideration is greater than unity: Since

All numbers lying between 1 and 10 i.e. numbers with 1 digit in the integral part have their logarithms lying between 0 and 1. Therefore, their integral parts are zero only.
All numbers lying between 10 and 100 have two digits in their integral parts. Their logarithms lie between 1 and 2. Therefore, numbers with two digits have integral parts with 1 as characteristic.
In general, the logarithm of a number containing n digits only in its integral parts is (n – 1) + a fraction. For example, the characteristics of log 75, log 79326, log 1.76 are 1, 4 and 0 respectively.
Negative characteristics
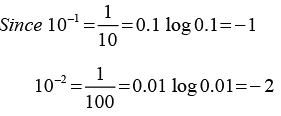
All numbers lying between 1 and 0.1 have logarithms lying between 0 and –1, i.e. greater than –1 and less than 0. Since the decimal part is always written positive, the characteristic is –1.
All numbers lying between 0.1 and 0.01 have their logarithms lying between –1 and –2 as characteristic of their logarithms.
In general, the logarithm of a number having n zeros just after the decimal point is – (n + 1) + a fraction.
Hence, we deduce that the characteristic of the logarithm of a number less than unity is one more than the number of zeros just after the decimal point and is negative.
Mantissa:
The mantissa is the fractional part of the logarithm of a given number

Thus with the same figures there will be difference in the characteristic only. It should be remembered, that the mantissa is always a positive quantity. The other way to indicate this is
Log .004594 = – 3 + .6625 = – 3.6625.
Negative mantissa must be converted into a positive mantissa before reference to a logarithm table. For example
– 3.6872 = – 4 + (4–3.6872) = 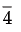 + 0.3128 =
+ 0.3128 = 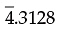 It may be noted that
It may be noted that  .3128 is different from – 4.3128 as – 4.3128 is a negative number whereas, in
.3128 is different from – 4.3128 as – 4.3128 is a negative number whereas, in  , 4 is negative while .3128 is positive.
, 4 is negative while .3128 is positive.
Illustration I: 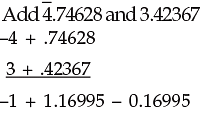
Antilogarithms:
If x is the logarithm of a given number n with a given base then n is called the antilogarithm (antilog) of x to that base.
This can be expressed as follows:-
If logan = x then n = antilog x
For example, if log 61720 = 4.7904 then 61720 = antilog 4.7904
Example 1: Find the value of log 5 if log 2 is equal to .3010
Solution : 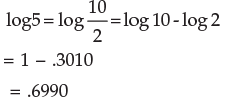
Example 2: Find the number whose logarithm is 2.4678.
Solution: From the antilog table, for mantissa .467, the number = 2931
for mean difference 8, the number = 5
∴ for mantissa .4678, the number = 2936
The characteristic is 2, therefore, the number must have 3 digits in the integral part.
Hence, Antilog 2.4678 = 293.6
Example 3: Find the number whose logarithm is –2.4678.
Solution: -2.4678 = - 3 + 3 − 2.4678 = − 3 + .5322 =  For mantissa .532, the number = 3404For mean difference 2, the number = 2
For mantissa .532, the number = 3404For mean difference 2, the number = 2
∴ for mantissa .5322, the number = 3406
The characteristic is –3, therefore, the number is less than one and there must be two zeros just after the decimal point.
Thus, Antilog (–2.4678) = 0.003406
Properties of Logarithm
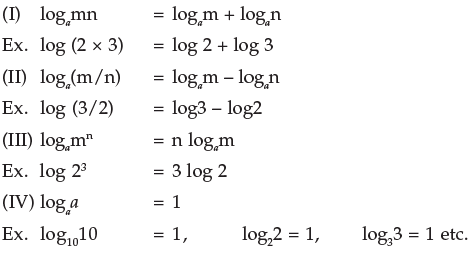

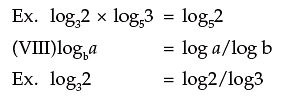
Note:
(A) If base is understood, base is taken as 10
(B) Thus log 10 = 1, log 1 = 0
(C) Logarithm using base 10 is called Common logarithm and logarithm using base e is called Natural logarithm {e = 2.33 (approx.) called exponential number}.
Relation between Indices and Logarithm
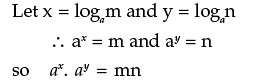

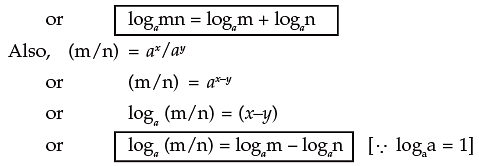

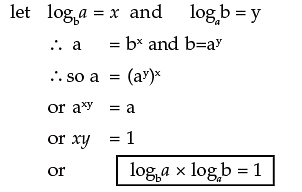
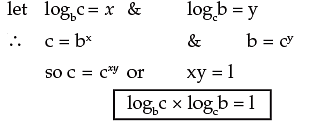
Example 1: Find the logarithm of 64 to the bas 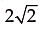
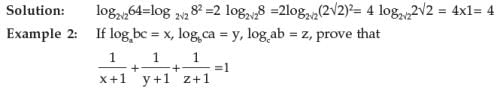
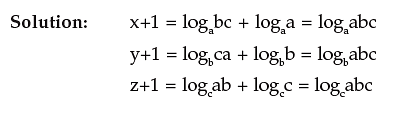
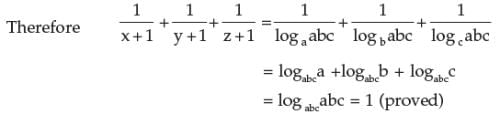
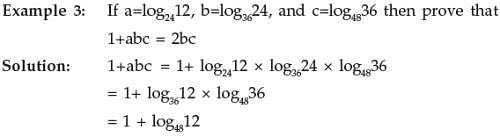
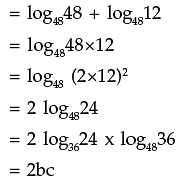
FAQs on ICAI Notes- Ratio and Proportion, Indices, Logarithms- 2 - CA Foundation
| 1. What is the definition of ratio and proportion in mathematics? |  |
| 2. How do you solve problems involving ratios and proportions? |  |
| 3. What are indices in mathematics? |  |
| 4. What are the properties of logarithms? |  |
| 5. How can logarithms be used in real-life applications? |  |

|
Explore Courses for CA Foundation exam
|

|


















