Ratio and Proportion Class 6 Worksheet Maths Chapter 12
Q1: Fill in the box :
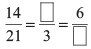
Ans: 2, 9
To find the missing values, we simplify the given ratio 14/21 to 2/3.
So, the first missing value is 2.
For the second missing value in the numerator of 6/___, we note that 2/3 is equivalent to 6/9, indicating the second missing value is 9.
Hence, the missing values are 2 and 9 respectively.
Q2: Find the ratio of the following :
(i) 21 hours to 49 hours __________
(ii) 75 cm to 3 m __________
(iii) A dozen to a score __________
(iv) 1 hour to 20 minutes __________
(v) A dozen to a gross __________
Ans:
(i) 21 : 49 = 3 : 7
(ii) 75 : 300 = 1 : 4
(iii) 12 : 20 = 3 : 5
(iv) 60 : 20 = 3 : 1
(v) 12 : 144 = 1 : 12
(i) To find the ratio of 21 hours to 49 hours, both numbers are divided by their greatest common divisor, which is 7. So, 21 ÷ 7 = 3 and 49 ÷ 7 = 7, resulting in the ratio 3 : 7.
(ii) To express 75 cm to 3 m in the same unit, we convert 3 m to cm (1 m = 100 cm), giving us 300 cm. Then, we simplify the ratio by dividing both numbers by their greatest common divisor, which is 75. So, 75 ÷ 75 = 1 and 300 ÷ 75 = 4, resulting in the ratio 1 : 4.
(iii) A dozen equals 12 and a score equals 20. We simplify the ratio by dividing both numbers by their greatest common divisor, which is 4. So, 12 ÷ 4 = 3 and 20 ÷ 4 = 5, giving us the ratio 3 : 5.
(iv) Converting 1 hour to minutes (1 hour = 60 minutes), we get 60 minutes. Then, we simplify the ratio by dividing both numbers by their greatest common divisor, which is 20. So, 60 ÷ 20 = 3 and 20 ÷ 20 = 1, resulting in the ratio 3 : 1.
(v) A dozen is 12 and a gross is 144. Simplifying the ratio by dividing both numbers by their greatest common divisor, which is 12, we get 12 ÷ 12 = 1 and 144 ÷ 12 = 12, giving us the ratio 1 : 12.
Q3: Write True or False :
(i) 2 : 8 :: 4 : 16 ( )
(ii) 500 : 200 :: 150 : 60 ( )
(iii) 50 : 45 :: 30 : 20 ( )
Ans:
(i) True
(ii) True
(iii) False
(i) This statement is true because both ratios simplify to 1:4.
(ii) This statement is true because both ratios simplify to 5:2.
(iii) This statement is false because the ratio 50:45 doesn't simplify to 30:20. They are not in proportion.
Q4: Fill in the blanks so that the numbers are in proportion :
(i) 20, 18, 40, ..............
(ii) ............., 35, 3, 15
(iii) 25, 100, ..........., 160
(iv) 32, ..........., 6, 12
Ans:
(i) 36
(ii) 7
(iii) 40
(iv) 64
(i) To find the missing number, we notice that 20 is 90% of 40 and 18 is 80% of 36. Applying this pattern, we find that 36 is 90% of 40, making it the missing number.
(ii) The missing number can be found by observing that 35 is 7 times greater than 5 and 3 is 7 times less than 21. So, 7 is the missing number.
(iii) By observing the pattern, we see that 25 is 25% of 100 and 160 is 25% more than 100. Thus, the missing number is 40.
(iv) The missing number can be found by realizing that 32 is 8 times greater than 4 and 6 is 8 times less than 48. Hence, 64 is the missing number.
Q5: Find x, if the numbers are in proportion :
(i) 3, 9, 9, x __________
(ii) 25, x, 1 , 4 __________
Ans:
(i) 27
(ii) 100
(i) The ratio between 3 and 9 is 1:3. Since the ratio between 9 and x is also 1:3, x must be 27 to maintain proportionality.
(ii) The ratio between 25 and 1 is 25:1, which simplifies to 25:1. To maintain proportionality, the ratio between x and 4 must also be 25:1. Hence, x equals 100.
Q6: Divide 60 in the ratio 1:2 between Bulbul and Kanika :
(i) Bulbul's share = __________
(ii) Kanika's share = __________
Ans:
(i) 20
(ii) 40
(i) Since the ratio between Bulbul and Kanika's shares is 1:2, Bulbul gets one-third (1/3) of 60, which is 20.
(ii) Kanika's share is two-thirds (2/3) of 60, which equals 40.
Q7: Give two equivalent ratios of 6 : 4
Ans: 3 : 2, 12 : 8 (or any other two equivalent ratios)
Equivalent ratios are obtained by multiplying or dividing both parts of a ratio by the same number. For example, to find another equivalent ratio for 6:4, we can divide both parts by 2, resulting in 3:2. Similarly, we can multiply both parts by 2 to get 12:8.
Q8: Weight of 80 books in 160 kg. What is the weight of 25 books?
Ans: 50 kg
To find the weight of 25 books, we divide the total weight of 80 books (160 kg) by 80 to get the weight of one book (2 kg). Then, we multiply the weight of one book by 25 to find the weight of 25 books, which equals 50 kg.
Q9: Divide 1200 among A, B and C in the ratios 4 : 5 : 6.
(i) A's share = __________
(ii) B's share = __________
(iii) C's share = __________
Ans:
(i) 320
(ii) 400
(iii) 480
To divide 1200 among A, B, and C in the ratios 4:5:6, we first find the total number of parts in the ratio, which is 4 + 5 + 6 = 15.
(i) To find A's share, we calculate (4/15) x 1200 = 320. This means A's share is 320.
(ii) To find B's share, we calculate (5/15) x 1200 = 400. This means B's share is 400.
(iii) To find C's share, we calculate (6/15) x 1200 = 480. This means C's share is 480.
So, A's share is 320, B's share is 400, and C's share is 480. Each person's share is in proportion to the ratio given.
In a class of 40 students, 15 like cricket, 20 like football, and 5 like both cricket and football. (Now answer question number 10 and 11)
Q10: Find the ratio of a number of students who like cricket to those who like football.
Ans: 15 : 20 = 3 : 4
Out of 40 students, 15 like cricket and 20 like football. To find the ratio between the number of students who like cricket to those who like football, we simplify the ratio between 15 and 20, which is 3:4.
Q11: Find the ratio of number of students who like football to those who like both.
Ans: 20 : 5 = 4 : 1
Out of 40 students, 20 like football, and 5 like both cricket and football. To find the ratio between the number of students who like football to those who like both, we simplify the ratio between 20 and 5, which is 4:1.
Q12: If 2, 5 and x are in proportion, find x __________ [Hint 2 : 5 :: 5: x]
Ans: 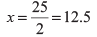
If 2, 5, and x are in proportion, it means 2 is to 5 as 5 is to x. Mathematically, we can express this as 2/5 = 5/x. Solving for x, we get x = (5 * 5) / 2 = 25 / 2 = 12.5.
Q13: Find the ratio of 5 days to 2 weeks.
Ans: 5 : 14
To find the ratio between 5 days and 2 weeks, we first convert weeks to days. Since 1 week = 7 days, 2 weeks = 2 * 7 = 14 days. Then, we simplify the ratio between 5 days and 14 days to get 5:14.
Q14: The cost of one dozen bananas is 60. Find the cost of 8 bananas.
Ans: 40
Since one dozen equals 12 bananas and costs 60, the cost of one banana is 60 / 12 = 5. To find the cost of 8 bananas, we multiply the cost of one banana by 8, giving us 5 * 8 = 40.
Q15: In a class of 48 students, there are 12 girls and rest are boys. Find the ratio of :
(i) Girls to Boys. __________
(ii) Girls to total number of students. __________
Ans:
(i) 12 : 36 = 1 : 3
(ii) 12 : 48 = 1 : 4
(i) Out of 48 students, 12 are girls. The rest, which is 48 - 12 = 36, are boys. So, the ratio of girls to boys is 12:36, which simplifies to 1:3.
(ii) The number of girls (12) compared to the total number of students (48) gives the ratio of girls to the total number of students, which is 12:48, simplifying to 1:4.
FAQs on Ratio and Proportion Class 6 Worksheet Maths Chapter 12
| 1. What is the difference between ratio and proportion? |  |
| 2. How can I solve problems involving ratio and proportion? |  |
| 3. Can you provide an example of a real-life application of ratios and proportions? |  |
| 4. What are some common mistakes to avoid when working with ratios and proportions? |  |
| 5. How do you simplify a ratio? |  |

















