Ratio and Proportion, Indices, Logarithms - 1 - CA Foundation PDF Download
RATIO AND PROPORTION, INDICES, LOGARITHMS
LEARNING OBJECTIVES
After reading this unit a student will learn –
- How to compute and compare two ratios;
- Effect of increase or decrease of a quantity on the ratio;
- The concept and application of inverse ratio.
We use ratio in many ways in practical fields. For example, it is given that a certain sum of money is divided into three parts in the given ratio. If first part is given then we can find out total amount and the other two parts.
In the case when ratio of boys and girls in a school is given and the total no. of student is also given, then if we know the no. of boys in the school, we can find out the no. of girls of that school by using ratios.
1.1 RATIO
A ratio is a comparison of the sizes of two or more quantities of the same kind by division.
If a and b are two quantities of the same kind (in same units), then the fraction a/b is called the ratio of a to b. It is written as a : b. Thus, the ratio of a to b = a/b or a : b. The quantities a and b are called the terms of the ratio, a is called the first term or antecedent and b is called the second term or consequent.
For example, in the ratio 5 : 6, 5 & 6 are called terms of the ratio. 5 is called first term and 6 is called second term.
1.1.2 REMARKS
- Both terms of a ratio can be multiplied or divided by the same (non–zero) number. Usually a ratio is expressed in lowest terms (or simplest form).
Illustration I:
12 : 16 = 12/16 = (3 × 4)/(4 × 4) = 3/4 = 3 : 4
- The order of the terms in a ratio is important.
Illustration II:
3 : 4 is not same as 4 : 3.
- Ratio exists only between quantities of the same kind.
Illustration III:
(i) There is no ratio between no. of students in a class and the salary of a teacher.
(ii) There is no ratio between the weight of one child and the age of another child.
- Quantities to be compared (by division) must be in the same units.
Illustration IV:

Illustration V:
(i) Ratio between 3 kg & 5 kg. = 3/5
- To compare two ratios, convert them into equivalent like fractions.
Illustration VI: To find which ratio is greater ——
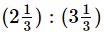 ; 3.6 : 4.8
; 3.6 : 4.8
Solution: 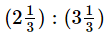 = 7/3 : 10/3 = 7 : 10 = 7/10
= 7/3 : 10/3 = 7 : 10 = 7/10
3.6 : 4.8 = 3.6/4.8 = 36/48 = 3/4
L.C.M of 10 and 4 is 20.
So, 7/10 = (7 × 2)/(10 × 2) = 14/20
And 3/4 = (3 × 5)/(4 × 5) = 15/20
As 15 > 14 so, 15/20 > 14/20 i. e. 3/4 > 7/10
Hence, 3.6 : 4.8 is greater ratio.
- If a quantity increases or decreases in the ratio a : b then new quantity = b of the original quantity/a
The fraction by which the original quantity is multiplied to get a new quantity is called the factor multiplying ratio.
Illustration VII: Rounaq weighs 56.7 kg. If he reduces his weight in the ratio 7 : 6, find his new weight.
Solution: Original weight of Rounaq = 56.7 kg.
He reduces his weight in the ratio 7 : 6
His new weight = (6 × 56.7)/7 = 6 × 8.1 = 48.6 kg.
Example 1: Simplify the ratio 1/3 : 1/8 : 1/6
Solution: L.C.M. of 3, 8 and 6 is 24.
1/3 : 1/8 : 1/6 = 1 × 24/3 : 1 × 24/8 : 1 × 24/6
= 8 : 3 : 4
Example 2: The ratio of the no. of boys to the no. of girls in a school of 720 students is 3 : 5. If 18 new girls are admitted in the school, find how many new boys may be admitted so that the
ratio of the no. of boys to the no. of girls may change to 2 : 3.
Solution: The ratio of the no. of boys to the no. of girls = 3 : 5
Sum of the ratios = 3 + 5 = 8
So, the no. of boys in the school = (3 × 720)/8 = 270
And the no. of girls in the school = (5 × 720)/8 = 450
Let the no. of new boys admitted be x, then the no. of boys become (270 + x).
After admitting 18 new girls, the no. of girls become 450 + 18 = 468
According to given description of the problem, (270 + x)/468 = 2/3
Or, 3 (270 + x) = 2 x 468
Or, 810 + 3x = 936 or, 3x = 126 or, x = 42.
Hence the no. of new boys admitted = 42.
1.1.3 INVERSE RATIO
One ratio is the inverse of another if their product is 1. Thus a : b is the inverse of b : a and vice– versa.
1. A ratio a : b is said to be of greater inequality if a>b and of less inequality if a<b.
2. The ratio compound of the two ratios a : b and c : d is ac : bd.
For example compound ratio of 3 : 4 and 5 : 7 is 15 : 28.
Compound ratio of 2 : 3, 5 : 7 and 4 : 9 is 40 : 189.
3. A ratio compounded of itself is called its duplicate ratio.
Thus a2 : b2 is the duplicate ratio of a : b.
Similarly, the triplicate ratio of a : b is a3 : b3.
For example, duplicate ratio of 2 : 3 is 4 : 9. Triplicate ratio of 2 : 3 is 8 : 27.
4. The sub–duplicate ratio of a : b is √a : √b and the sub triplicate ratio of a : b is 
For example sub duplicate ratio of 4 : 9 is √4 : √9 = 2 : 3
And sub triplicate ratio of 8 : 27 is  = 2 : 3.
= 2 : 3.
5. If the ratio of two similar quantities can be expressed as a ratio of two integers, the quantities are said to be commensurable; otherwise, they are said to be incommensurable. √3 : √2 cannot be expressed as the ratio of two integers and therefore, √3 and √2 are incommensurable quantities.
6. Continued Ratio is the relation (or compassion) between the magnitudes of three or more quantities of the same kind. The continued ratio of three similar quantities a, b, c is written as a: b: c.
Illustration I: The continued ratio of Rs. 200, Rs. 400 and Rs. 600 is Rs. 200 : Rs. 400 : Rs. 600 = 1 : 2 : 3.
Example 1: The monthly incomes of two persons are in the ratio 4 : 5 and their monthly expenditures are in the ratio 7 : 9. If each saves Rs. 50 per month, find their monthly incomes.
Solution: Let the monthly incomes of two persons be Rs. 4x and Rs. 5x so that the ratio is Rs. 4x : Rs. 5x = 4 : 5. If each saves Rs. 50 per month, then the expenditures of two persons are Rs. (4x – 50) and Rs. (5x – 50).
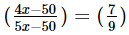 or, 36x 450 = 35x 350
or, 36x 450 = 35x 350
or, 36x – 35x = 450 – 350, or, x = 100
Hence, the monthly incomes of the two persons are Rs. 4 × 100 and Rs. 5 × 100 i.e.
Rs. 400 and Rs. 500.
Example 2 : The ratio of the prices of two houses was 16 : 23. Two years later when the price of the first has increased by 10% and that of the second by Rs. 477, the ratio of the prices becomes 11 : 20. Find the original prices of the two houses.
Solution: Let the original prices of two houses be Rs. 16x and Rs. 23x respectively. Then by the given conditions,

or, 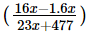 or, 320x + 32x = 253x + 5247
or, 320x + 32x = 253x + 5247
or, 352x – 253x = 5247, or, 99x = 5247; ∴ x = 53
Hence, the original prices of two houses are Rs. 16 × 53 and Rs. 23 × 53 i.e. Rs. 848 and Rs. 1,219.
Example 3 : Find in what ratio will the total wages of the workers of a factory be increased or decreased if there be a reduction in the number of workers in the ratio 15 : 11 and an increment in their wages in the ratio 22 : 25.
Solution: Let x be the original number of workers and Rs. y the (average) wages per workers.
Then the total wages before changes = Rs. xy.
After reduction, the number of workers = (11 x)/15 After increment, the (average) wages per workers = Rs. (25 y)/22
∴ The total wages after changes = 
Thus, the total wages of workers get decreased from Rs. xy to Rs. 5xy/6
Hence, the required ratio in which the total wages decrease is xy : 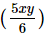 = 6:5.
= 6:5.
1.2 PROPORTION
LEARNING OBJECTIVES
After reading this unit, a student will learn –
- What is proportion?
- Properties of proportion and how to use them.
If the income of a man is increased in the given ratio and if the increase in his income is given then to find out his new income, Proportion problem is used.
Again if the ages of two men are in the given ratio and if the age of one man is given, we can find out the age of another man by Proportion.
An equality of two ratios is called a proportion. Four quantities a, b, c, d are said to be in proportion if a : b = c : d (also written as a : b :: c : d) i.e. if a/b = c/d i.e. if ad = bc.
The quantities a, b, c, d are called terms of the proportion; a, b, c and d are called its first, second, third and fourth terms respectively. First and fourth terms are called extremes (or extreme terms). Second and third terms are called means (or middle terms).
If a : b = c : d then d is called fourth proportional.
If a : b = c : d are in proportion then a/b = c/d i.e. ad = bc
i.e. product of extremes = product of means.
This is called cross product rule.
Three quantities a, b, c of the same kind (in same units) are said to be in continuous proportion if a : b = b : c i.e. a/b = b/c i.e. b2 = ac
If a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.
Thus, if b is mean proportional between a and c, then b2 = ac i.e. b = 
When three or more numbers are so related that the ratio of the first to the second, the ratio of the second to the third, third to the fourth etc. are all equal, the numbers are said to be in continued proportion. We write it as
x/y = y/z = z/w = w/p = p/q
when
x, y, z, w, p and q are in continued proportion. If a ratio is equal to the reciprocal of the other, then either of them is in inverse (or reciprocal) proportion of the other. For example 5/4 is in inverse proportion of 4/5 and vice–versa.
Note: In a ratio a : b, both quantities must be of the same kind while in a proportion a : b = c : d, all the four quantities need not be of the same type. The first two quantities should be of the same kind and last two quantities should be of the same kind.
Illustration I:
Rs. 6 : Rs. 8 = 12 toffees : 16 toffees are in a proportion.
Here 1st two quantities are of same kind and last two are of same kind.
Example 1: The nos. 2.4, 3.2, 1.5, 2 are in proportion because these nos. satisfy the property the product of extremes = product of means.
Here 2.4 × 2 = 4.8 and 3.2 × 1.5 = 4.8
Example 2: Find the value of x if 10/3 : x : : 5/2 : 5/4 Solution: 10/3 : x = 5/2 : 5/4
Using cross product rule, x × 5/2 = (10/3) × 5/4
Or, x = (10/3) × (5/4) × (2/5) = 5/3
Example 3: Find the fourth proportional to 2/3, 3/7, 4
Solution: Let the fourth proportional be x then 2/3, 3/7, 4, x are in proportion.
Using cross product rule, (2/3) × x = (3 × 4)/7
Or, x = (3 × 4 × 3)/(7 × 2) = 18/7.
Example 4: Find the third proportion to 2.4 kg, 9.6 kg
Solution: Let the third proportion to 2.4 kg, 9.6 kg be x kg.
Then 2.4 kg, 9.6 kg and x kg are in continued proportion since b2 = ac
So, 2.4/9.6 = 9.6/x or, x = (9.6 × 9.6)/2.4 = 38.4
Hence the third proportional is 38.4 kg.
Example 5: Find the mean proportion between 1.25 and 1.8
Solution: Mean proportion between 1.25 and 1.8 is 
1.2.1 PROPERTIES OF PROPORTION
1. If a : b = c : d, then ad = bc
2. Proof. 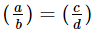 ; ad = bc (By cross - multiplication)
; ad = bc (By cross - multiplication)
Hence, b : a = d : c.
3. If a : b = c : d, then a : c = b : d (Alternendo)

4. If a : b = c : d, then a + b : b = c + d : d (Componendo)

5. If a : b = c : d, then a – b : b = c – d : d (Dividendo)

6. If a : b = c : d, then a + b : a – b = c + d : c – d (Componendo and Dividendo)

Dividing (1) by (2) we get

7. If a : b = c : d = e : f = ………………..….., then each of these ratios (Addendo) is equal (a + c + e + ……..) : (b + d + f + …….)

Example 1: If a : b = c : d = 2.5 : 1.5, what are the values of ad : bc and a+c : b+d?
Solution: 

Hence, the values of ad : bc and a + c : b + d are 1 : 1 and 5 : 3 respectively.

Example 3: A dealer mixes tea costing Rs. 6.92 per kg. with tea costing Rs. 7.77 per kg. and sells the mixture at Rs. 8.80 per kg. and earns a profit of 1712% on his sale price. In what proportion does he mix them?
Solution: Let us first find the cost price (C.P.) of the mixture. If S.P. is Rs. 100, profit is

If S.P. is Rs. 8.80, C.P. is (165 × 8.80)/(2 × 100) = Rs. 7.26
∴ C.P. of the mixture per kg = Rs. 7.26
2nd difference = Profit by selling 1 kg. of 2nd kind @ Rs. 7.26
= Rs. 7.77 – Rs. 7.26 = 51 paise
1st difference = Rs. 7.26 – Rs. 6.92 = 34 paise
We have to mix the two kinds in such a ratio that the amount of profit in the first case must balance the amount of loss in the second case.
Hence, the required ratio = (2nd diff) : (1st diff.) = 51 : 34 = 3 : 2.
1.2.2 LAWS ON PROPORTION AS DERIVED EARLIER
(i) p : q = r : s => q : p = s : r (Invertendo)
(p/q = r/s) => (q/p = s/r)
(ii) a : b = c : d => a : c = b : d (Alternendo)
(a/b = c/d) => (a/c = b/d)
(iii) a : b = c : d => a+b : b = c+d : d (Componendo)
(a/b = c/d) => (a+b)/b = (c+d)/d
(iv) a : b = c : d => a–b : b = c–d : d (Dividendo)
(a/b = c/d) => (a–b)/b = (c–d)/d
(v) a : b = c : d => a+b : a–b = c+d : c–d (Componendo & Dividendo)
(a+b)/(a–b) = (c+d)/(c–d)
(vi) a : b = c : d = a+c : b+d (Addendo)
(a/b = c/d = a+c/b+d)
(vii) a : b = c : d = a–c : b–d (Subtrahendo)
(a/b = c/d = a–c/b–d)
(viii) If a : b = c : d = e : f = ............ then each of these ratios = (a – c – e – .......) : (b – d – f – .....)
Proof: The reader may try it as an exercise (Subtrahendo) as the proof is similar to that derival in 7 above
FAQs on Ratio and Proportion, Indices, Logarithms - 1 - CA Foundation
| 1. What are ratios and proportions? |  |
| 2. How do you simplify ratios and proportions? |  |
| 3. What are indices and how do they work? |  |
| 4. How do you solve logarithmic equations? |  |
| 5. What are common logarithms and natural logarithms? |  |

|
Explore Courses for CA Foundation exam
|

|


















