Recursion | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
What is Recursion?
The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called as recursive function. Using recursive algorithm, certain problems can be solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc.
A Mathematical Interpretation
Let us consider a problem that a programmer have to determine the sum of first n natural numbers, there are several ways of doing that but the simplest approach is simply add the numbers starting from 1 to n. So the function simply looks like,
approach(1) – Simply adding one by one
f(n) = 1 + 2 + 3 +……..+ n
but there is another mathematical approach of representing this,
approach(2) – Recursive adding
f(n) = 1 n=1
f(n) = n + f(n-1) n>1
There is a simple difference between the approach (1) and approach(2) and that is in approach(2) the function “ f( ) ” itself is being called inside the function, so this phenomenon is named as recursion and the function containing recursion is called recursive function, at the end this is a great tool in the hand of the programmers to code some problems in a lot easier and efficient way.
What is base condition in recursion?
In the recursive program, the solution to the base case is provided and the solution of the bigger problem is expressed in terms of smaller problems.
int fact(int n)
{
if (n < = 1) // base case
return 1;
else
return n*fact(n-1);
}
In the above example, base case for n < = 1 is defined and larger value of number can be solved by converting to smaller one till base case is reached.
How a particular problem is solved using recursion?
The idea is to represent a problem in terms of one or more smaller problems, and add one or more base conditions that stop the recursion. For example, we compute factorial n if we know factorial of (n-1). The base case for factorial would be n = θ. We return 1 when n = 0.
Why Stack Overflow error occurs in recursion?
If the base case is not reached or not defined, then the stack overflow problem may arise. Let us take an example to understand this.
int fact(int n)
{
// wrong base case (it may cause
// stack overflow).
if (n == 100)
return 1;
else
return n*fact(n-1);
}
If fact(10) is called, it will call fact(9), fact(8), fact(7) and so on but the number will never reach 100. So, the base case is not reached. If the memory is exhausted by these functions on the stack, it will cause a stack overflow error.
What is the difference between direct and indirect recursion?
A function fun is called direct recursive if it calls the same function fun. A function fun is called indirect recursive if it calls another function say fun_new and fun_new calls fun directly or indirectly. Difference between direct and indirect recursion has been illustrated in Table 1.
// An example of direct recursion
void directRecFun()
{
// Some code....
directRecFun();
// Some code...
}
// An example of indirect recursion
void indirectRecFun1()
{ // Some code...
indirectRecFun2();
// Some code...
}
void indirectRecFun2()
{
// Some code...
indirectRecFun1();
// Some code...
}
What is difference between tailed and non-tailed recursion?
A recursive function is tail recursive when recursive call is the last thing executed by the function.
How memory is allocated to different function calls in recursion?
When any function is called from main(), the memory is allocated to it on the stack. A recursive function calls itself, the memory for a called function is allocated on top of memory allocated to calling function and different copy of local variables is created for each function call. When the base case is reached, the function returns its value to the function by whom it is called and memory is de-allocated and the process continues.
Let us take the example how recursion works by taking a simple function:
CPP
// A C++ program to demonstrate working of
// recursion
#include <bits/stdc++.h>
using namespace std;
void printFun(int test)
{
if (test < 1)
return;
else {
cout << test << " ";
printFun(test - 1); // statement 2
cout << test << " ";
return;
}
}
// Driver Code
int main()
{
int test = 3;
printFun(test);
}
Java
// A Java program to demonstrate working of
// recursion
class GFG {
static void printFun(int test)
{
if (test < 1)
return;
else {
System.out.printf("%d ", test);
printFun(test - 1); // statement 2
System.out.printf("%d ", test);
return;
}
}
// Driver Code
public static void main(String[] args)
{
int test = 3;
printFun(test);
}
}
// This code is contributed by
// Smitha Dinesh Semwal
Python3
# A Python 3 program to
# demonstrate working of
# recursion
def printFun(test):
if (test < 1):
return
else:
print(test, end=" ")
printFun(test-1) # statement 2
print(test, end=" ")
return
# Driver Code
test = 3
printFun(test)
# This code is contributed by
# Smitha Dinesh Semwal
C#
// A C# program to demonstrate
// working of recursion
using System;
class GFG {
// function to demonstrate
// working of recursion
static void printFun(int test)
{
if (test < 1)
return;
else {
Console.Write(test + " ");
// statement 2
printFun(test - 1);
Console.Write(test + " ");
return;
}
}
// Driver Code
public static void Main(String[] args)
{
int test = 3;
printFun(test);
}
}
// This code is contributed by Anshul Aggarwal.
PHP
<?php
// PHP program to demonstrate
// working of recursion
// function to demonstrate
// working of recursion
function printFun($test)
{
if ($test < 1)
return;
else
{
echo("$test ");
// statement 2
printFun($test-1);
echo("$test ");
return;
}
}
// Driver Code
$test = 3;
printFun($test);
// This code is contributed by
// Smitha Dinesh Semwal.
?>
Javascript
<script>
// JavaScript program to demonstrate working of
// recursion
function printFun(test)
{
if (test < 1)
return;
else {
document.write(test + " ");
printFun(test - 1); // statement 2
document.write(test + " ");
return;
}
}
// Driver code
let test = 3;
printFun(test);
</script>
Output :
3 2 1 1 2 3
When printFun(3) is called from main(), memory is allocated to printFun(3) and a local variable test is initialized to 3 and statement 1 to 4 are pushed on the stack as shown in below diagram. It first prints ‘3’. In statement 2, printFun(2) is called and memory is allocated to printFun(2) and a local variable test is initialized to 2 and statement 1 to 4 are pushed in the stack. Similarly, printFun(2) calls printFun(1) and printFun(1) calls printFun(0). printFun(0) goes to if statement and it return to printFun(1). Remaining statements of printFun(1) are executed and it returns to printFun(2) and so on. In the output, value from 3 to 1 are printed and then 1 to 3 are printed. The memory stack has been shown in below diagram.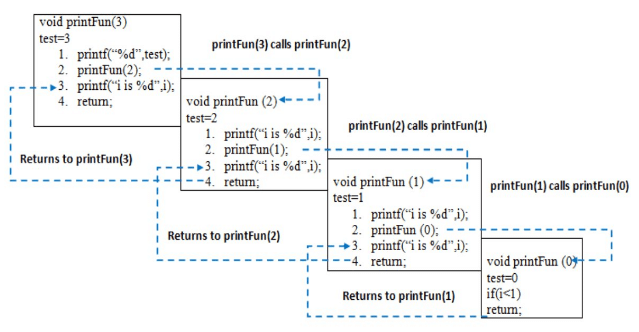 Now, let’s discuss a few practical problems which can be solved by using recursion and understand its basic working. For basic understanding please read the following articles.
Now, let’s discuss a few practical problems which can be solved by using recursion and understand its basic working. For basic understanding please read the following articles.
Basic understanding of Recursion.
Problem 1: Write a program and recurrence relation to find the Fibonacci series of n where n>2 .
Mathematical Equation:
n if n == 0, n == 1;
fib(n) = fib(n-1) + fib(n-2) otherwise;
Recurrence Relation:
T(n) = T(n-1) + T(n-2) + O(1)
Recursive program:
Input: n = 5
Output:
Fibonacci series of 5 numbers is : 0 1 1 2 3
Implementation:
C++
// C++ code to implement Fibonacci series
#include <bits/stdc++.h>
using namespace std;
// Function for fibonacci
int fib(int n)
{
// Stop condition
if (n == 0)
return 0;
// Stop condition
if (n == 1 || n == 2)
return 1;
// Recursion function
else
return (fib(n - 1) + fib(n - 2));
}
// Driver Code
int main()
{
// Initialize variable n.
int n = 5;
cout<<"Fibonacci series of 5 numbers is: ";
// for loop to print the fiboancci series.
for (int i = 0; i < n; i++)
{
cout<<fib(i)<<" ";
}
return 0;
}
C
// C code to implement Fibonacci series
#include <stdio.h>
// Function for fibonacci
int fib(int n)
{
// Stop condition
if (n == 0)
return 0;
// Stop condition
if (n == 1 || n == 2)
return 1;
// Recursion function
else
return (fib(n - 1) + fib(n - 2));
}
// Driver Code
int main()
{
// Initialize variable n.
int n = 5;
printf("Fibonacci series "
"of %d numbers is: ",
n);
// for loop to print the fiboancci series.
for (int i = 0; i < n; i++) {
printf("%d ", fib(i));
}
return 0;
}
Java
// Java code to implement Fibonacci series
import java.util.*;
class GFG
{
// Function for fibonacci
static int fib(int n)
{
// Stop condition
if (n == 0)
return 0;
// Stop condition
if (n == 1 || n == 2)
return 1;
// Recursion function
else
return (fib(n - 1) + fib(n - 2));
}
// Driver Code
public static void main(String []args)
{
// Initialize variable n.
int n = 5;
System.out.print("Fibonacci series of 5 numbers is: ");
// for loop to print the fiboancci series.
for (int i = 0; i < n; i++)
{
System.out.print(fib(i)+" ");
}
}
}
// This code is contributed by rutvik_56.
Python3
# Python code to implement Fibonacci series
# Function for fibonacci
def fib(n):
# Stop condition
if (n == 0):
return 0
# Stop condition
if (n == 1 or n == 2):
return 1
# Recursion function
else:
return (fib(n - 1) + fib(n - 2))
# Driver Code
# Initialize variable n.
n = 5;
print("Fibonacci series of 5 numbers is :",end=" ")
# for loop to print the fiboancci series.
for i in range(0,n):
print(fib(i),end=" ")
C#
using System;
public class GFG
{
// Function for fibonacci
static int fib(int n)
{
// Stop condition
if (n == 0)
return 0;
// Stop condition
if (n == 1 || n == 2)
return 1;
// Recursion function
else
return (fib(n - 1) + fib(n - 2));
}
// Driver Code
static public void Main ()
{
// Initialize variable n.
int n = 5;
Console.Write("Fibonacci series of 5 numbers is: ");
// for loop to print the fiboancci series.
for (int i = 0; i < n; i++)
{
Console.Write(fib(i) + " ");
}
}
}
// This code is contributed by avanitrachhadiya2155
Javascript
<script>
// JavaScript code to implement Fibonacci series
// Function for fibonacci
function fib(n)
{
// Stop condition
if(n == 0)
return 0;
// Stop condition
if(n == 1 || n == 2)
return 1;
// Recursion function
else
return fib(n-1) + fib(n-2);
}
// Initialize variable n.
let n = 5;
document.write("Fibonacci series of 5 numbers is: ");
// for loop to print the fiboancci series.
for(let i = 0; i < n; i++)
{
document.write(fib(i) + " ");
}
</script>
Output
Fibonacci series of 5 numbers is: 0 1 1 2 3
Here is the recursive tree for input 5 which shows a clear picture of how a big problem can be solved into smaller ones.
fib(n) is a Fibonacci function. The time complexity of the given program can depend on the function call.
fib(n) -> level CBT (UB) -> 2^n-1 nodes -> 2^n function call -> 2^n*O(1) -> T(n) = O(2^n)
For Best Case.
T(n) = 0(2^n\2)
Working: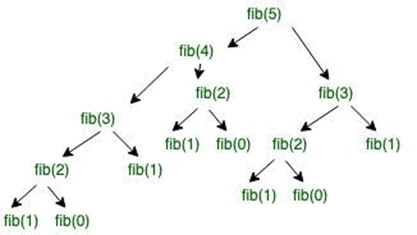
Problem 2: Write a program and recurrence relation to find the Factorial of n where n>2 .
Mathematical Eqution:
1 if n == 0 or n == 1;
f(n) = n*f(n-1) if n> 1;
Recurrence Relation:
T(n) = 1 for n = 0
T(n) = 1 + T(n-1) for n > 0
Recursive Program:
Input: n = 5
Output:
factorial of 5 is: 120
Implementation:
C++
// C++ code to implement factorial
#include <bits/stdc++.h>
using namespace std;
// Factorial function
int f(int n)
{
// Stop condition
if (n == 0 || n == 1)
return 1;
// Recursive condition
else
return n * f(n - 1);
}
// Driver code
int main()
{
int n = 5;
cout<<"factorial of "<<n<<" is: "<<f(n);
return 0;
}
C
// C code to implement factorial
#include <stdio.h>
// Factorial function
int f(int n)
{
// Stop condition
if (n == 0 || n == 1)
return 1;
// Recursive condition
else
return n * f(n - 1);
}
// Driver code
int main()
{
int n = 5;
printf("factorial of %d is: %d", n, f(n));
return 0;
}
Java
// Java code to implement factorial
public class GFG
{
// Factorial function
static int f(int n)
{
// Stop condition
if (n == 0 || n == 1)
return 1;
// Recursive condition
else
return n * f(n - 1);
}
// Driver code
public static void main(String[] args)
{
int n = 5;
System.out.println("factorial of " + n + " is: " + f(n));
}
}
// This code is contributed by divyesh072019.
Python3
# Python3 code to implement factorial
# Factorial function
def f(n):
# Stop condition
if (n == 0 or n == 1):
return 1;
# Recursive condition
else:
return n * f(n - 1);
# Driver code
if __name__=='__main__':
n = 5;
print("factorial of",n,"is:",f(n))
# This code is contributed by pratham76.
C#
// C# code to implement factorial
using System;
class GFG {
// Factorial function
static int f(int n)
{
// Stop condition
if (n == 0 || n == 1)
return 1;
// Recursive condition
else
return n * f(n - 1);
}
// Driver code
static void Main()
{
int n = 5;
Console.WriteLine("factorial of " + n + " is: " + f(n));
}
}
// This code is contributed by divyeshrabadiya07.
Javascript
<script>
// JavaScript code to implement factorial
// Factorial function
function f(n)
{
// Stop condition
if(n == 0 || n == 1)
return 1;
// Recursive condition
else
return n*f(n-1);
}
// Initialize variable n.
let n = 5;
document.write("factorial of "+ n +" is: " + f(n));
// This code is contributed by probinsah.
</script>
Output:
factorial of 5 is: 120
Working: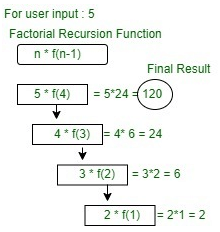 Diagram of factorial Recursion function for user input 5.
Diagram of factorial Recursion function for user input 5.
What are the disadvantages of recursive programming over iterative programming?
Note that both recursive and iterative programs have the same problem-solving powers, i.e., every recursive program can be written iteratively and vice versa is also true. The recursive program has greater space requirements than iterative program as all functions will remain in the stack until the base case is reached. It also has greater time requirements because of function calls and returns overhead.
What are the advantages of recursive programming over iterative programming?
Recursion provides a clean and simple way to write code. Some problems are inherently recursive like tree traversals, Tower of Hanoi, etc. For such problems, it is preferred to write recursive code. We can write such codes also iteratively with the help of a stack data structure. For example refer Inorder Tree Traversal without Recursion, Iterative Tower of Hanoi.
|
120 docs|30 tests
|
FAQs on Recursion - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is recursion in computer programming? |  |
| 2. How does recursion work in programming? |  |
| 3. What are the advantages of using recursion in programming? |  |
| 4. What are the limitations of recursion in programming? |  |
| 5. Are there any alternatives to using recursion in programming? |  |























