Refraction & Reflection of a Plane Wave at a Plane Surface - Electronics and Communication Engineering (ECE) PDF Download
Introduction
Reflection is the process by which light falls on a surface and bounces back. Read on to understand the refraction and reflection of plane waves at a plane surface using wavefronts.Refraction of a wave
Waves change direction when they pass from one medium to another. This phenomenon is called refraction. Refraction can occur in different types of mediums like sound, water, etc. Refraction is the bending of light waves. The amount of refraction depends on the change in the speed of light and the angle at which the waves are bending.Snell’s law shows the relationship between angles of incidence and refraction, and the refractive index of each medium. The refractive index refers to the extent to which a medium can increase or decrease the speed of light. The image below shows how refraction works.
According to Snell’s law,
n1Sinθ1= n2Sinθ2
where n1 is the refractive index of medium 1 and n2 is the refractive index of medium 2. θ1 is the angle of incidence and θ2 is the angle of refraction.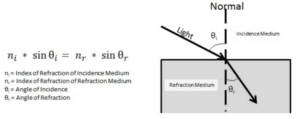
Reflection of a wave
Reflection of a wave occurs when a ray of light hits an opaque surface and bounces back. Like refraction, reflection can also occur in different types of waves like sound, infrared waves, radio waves, etc. There are two types of reflection: - Specular Reflection: A ray of light falls on a smooth surface, the light bounces or reflects off the surface at the same angle.
- Diffuse Reflection: A ray of light falls on a surface in a way that the light bounces back or reflects off the surface at various angles.
- There are laws of reflection that determine how the light rays behave when striking a surface. It is imperative to understand the following three things to have a better understanding of these laws:
- Incident ray: A ray of light that is moving towards the surface.
- Reflected ray: A ray of light that bounces back after hitting the surface.
- Normal Line: A line that is perpendicular to the surface and divides the incident and reflected ray into two equal angles–angle of reflection and angle of incidence.
- As per the law of reflection when a ray of light reflects off a surface, the angle of incidence is equal to the angle of reflection.
All these angles lie on the same surface. The image below shows the laws of reflection and how it works.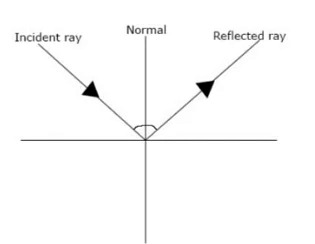
Wavefront
A wavefront can be defined as the centre of all the points in a medium where all the waves are in the same phase. Wavefronts are of three types:- Spherical wavefront: This is formed when the source of light is small, the wavefront formed will be spherical.
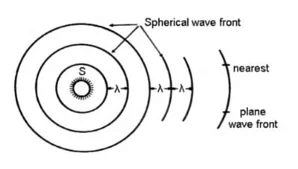
- Plane wavefront: This is formed when the small part of the spherical or cylindrical wavefront originated from an unmeasurable or infinite source of light. For example, the light from the Sun.
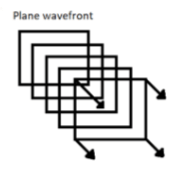
- Cylindrical wavefront: This is formed when the source of light is a line source.
Huygen’s principle
One major concept that you need to understand for the reflection and refraction of plane waves at a plane surface is Huygen’s Principle. In 1670, Christian Huygen came up with a theory that explained how waves propagated.According to Huygen, every point on a wavefront is a source of secondary wavelets that spread out in a forward direction at the speed of the wave itself. The new wavefront is the sum of all the secondary wavelets.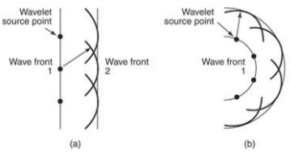 According to Huygen’s Principle, a plane light wave moves through free space at the speed of light. The light waves associated with this wavefront also move in a straight line as shown in the image below.
According to Huygen’s Principle, a plane light wave moves through free space at the speed of light. The light waves associated with this wavefront also move in a straight line as shown in the image below.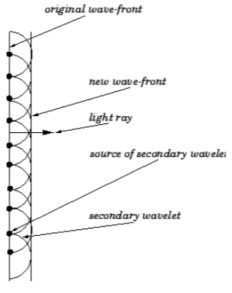 Figure info: Reflection of plane wave at plane surface using wavefront
Figure info: Reflection of plane wave at plane surface using wavefront
Consider the image shown below, where plane wavefront AB, on the surface XY, where AB is the incident ray reflecting on the surface at point A.
PA and QBC are perpendiculars drawn to points A and B respectively, making them incident rays. AN is the normal line drawn on the surface. According to Huygen’s Principle, A and B will act as a source of multiple secondary wavelets. Consider A and B as sources for secondary wavelets. The time taken for the secondary wavelets to travel the distance BC from point B is the same time taken for secondary wavelets from A to travel the distance BC after reflection. This makes CD the reflected plane wave and AD the reflected ray.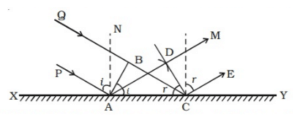 Now, we can see the incident wavefront AB, the reflected ray CD and the surface XY are on the same plane. Refer to the image below to see how Huygen’s Principle is used to explain Laws of Reflection.
Now, we can see the incident wavefront AB, the reflected ray CD and the surface XY are on the same plane. Refer to the image below to see how Huygen’s Principle is used to explain Laws of Reflection.
Angle of incidence i = ∠PAN = 90° – ∠NAB = ∠BAC
Angle of reflection r = ∠NAD = 90° – ∠DAC = ∠DCA
In right angled triangles ABC and ADC
∠B = ∠D = 90°
BC = AD and AC is common
The two triangles are congruent
∠BAC = ∠DCA
i.e. i = r
Thus the angle of incidence is equal to the angle of reflection.
Refraction of plane wave at plane surface using wavefront
Let XY be a plane reflecting surface and AB be a plane wavefront incident on the surface at A. PA and QBC are perpendiculars drawn to AB at A and B respectively. Hence they represent incident rays. AN is the normal drawn to the surface. The wave front and the surface are perpendicular to the plane of the paper.Consider the diagram below.
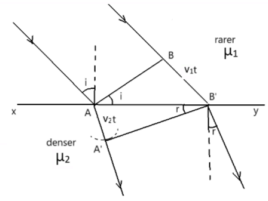
Consider a plane wavefront XY that separates the rare medium ( μ1) from the denser medium (μ2). Here, the velocities of the incident ray and refracted ray of the rare medium and denser medium can be v1 and v2 respectively. The velocity of the waves depends upon the medium. Following Huygen’s Principle, A and B form the source of secondary spherical wavelets. Here, ‘t’ can be the time taken from B to reach B’.
So in medium 1, BB’ = v1t.
Simultaneously, the secondary wavelets originating from point A will travel the same distance in the denser medium to A’. Therefore,
AA’= v2t in medium 2.
Now A’B’ are the secondary wavefronts at time t.
Sin i / Sin r= (BB’/AB’) / (AA’/AB’)
= BB’/AA’
= v1t/v2t
= v1/v2
= μ which is a constant.
μ is the reflective index of the medium. The refractive index is the ratio of the velocity of light in a vacuum to the velocity of light in another medium. Thus, this proves Snell’s law of refraction using plane waves and Huygen’s Principle.



















