Regular Expressions & Finite Automata | GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Computer Science Engineering (CSE) PDF Download
Finite Automata - Introduction
Finite Automata(FA) is the simplest machine to recognize patterns. Finite automata are a foundational concept in the theory of computation and are used to model and design computer programs and digital circuits.
A Finite Automata consists of the following :
Q : Finite set of states.
∑ : set of Input Symbols.
q : Initial state.
F : set of Final States.
δ : Transition Function.
Formal specification of machine is
{ Q, ∑, q, F, δ }.
FA is characterized into two types:
- Deterministic Finite Automata (DFA)
- Nondeterministic Finite Automata (NFA)
Deterministic Finite Automata (DFA)
DFA consists of 5 tuples {Q, ∑, q, F, δ}.
Q : set of all states.
∑ : set of input symbols. ( Symbols which machine takes as input )
q : Initial state. ( Starting state of a machine )
F : set of final state.
δ : Transition Function, defined as δ : Q X ∑ --> Q.
The features of DFA are:
1. In a DFA, for a particular input character, the machine goes to one state only. A transition function is defined on every state for every input symbol.
2. Also in DFA null (or ε) move is not allowed, i.e., DFA can not change state without any input character.
For example, below DFA with ∑ = {0, 1} accepts all strings ending with 0.
One important thing to note is, there can be many possible DFAs for a pattern. A DFA with minimum number of states is generally preferred.
Nondeterministic Finite Automata (NFA)
NFA is similar to DFA except following additional features:
1. Null (or ε) move is allowed i.e., it can move forward without reading symbols.
2. Ability to transit to any number of states for a particular input.
However, these above features don’t add any power to NFA. If we compare both in terms of power, both are equivalent.
Due to the above additional features, NFA has a different transition function, the rest is the same as DFA.
δ: Transition Function
δ: Q X (∑ U ϵ ) --> 2 ^ Q.
As you can see in the transition function for any input including null (or &epsilon), NFA can go to any state number of states.
For example, below is a NFA for the above problem
Note: One important thing to note is, in NFA, if any path for an input string leads to a final state, then the input string accepted. For example, in above NFA, there are multiple paths for input string “00”. Since, one of the paths leads to a final state, “00” is accepted by above NFA.
Some Important Points:
1. Every DFA is NFA but not vice versa.
2. Both NFA and DFA have the same power and each NFA can be translated into a DFA.
3. There can be multiple final states in both DFA and NFA.
3. NFA is more of a theoretical concept.
4. DFA is used in Lexical Analysis in Compiler.
Regular Expressions, Regular Grammar and Regular Languages
As discussed in Chomsky Hierarchy, Regular Languages are the most restricted types of languages and are accepted by finite automata.
Regular Expressions
Regular Expressions are used to denote regular languages. An expression is regular if:
- ɸ is a regular expression for regular language ɸ.
- ɛ is a regular expression for regular language {ɛ}.
- If a ∈ Σ (Σ represents the input alphabet), a is regular expression with language {a}.
- If a and b are regular expression, a + b is also a regular expression with language {a,b}.
- If a and b are regular expression, ab (concatenation of a and b) is also regular.
- If a is regular expression, a* (0 or more times a) is also regular.
Regular Grammar:
A grammar is regular if it has rules of form A -> a or A -> aB or A -> ɛ where ɛ is a special symbol called NULL.
Regular Languages:
A language is regular if it can be expressed in terms of the regular expression.Closure Properties of Regular Language
- Union: If L1 and L2 are two regular languages, their union L1 ∪ L2 will also be regular. For example, L1 = {an | n ≥ 0} and L2 = {bn | n ≥ 0}
L3 = L1 ∪ L2 = {an ∪ bn | n ≥ 0} is also regular. - Intersection: If L1 and L2 are two regular languages, their intersection L1 ∩ L2 will also be regular. For example,
L1= {am bn | n ≥ 0 and m ≥ 0} and L2= {am bn ∪ bn am | n ≥ 0 and m ≥ 0}
L3 = L1 ∩ L2 = {am bn | n ≥ 0 and m ≥ 0} is also regular. - Concatenation: If L1 and L2 are two regular languages, their concatenation L1.L2 will also be regular. For example,
L1 = {an | n ≥ 0} and L2 = {bn | n ≥ 0}
L3 = L1.L2 = {am . bn | m ≥ 0 and n ≥ 0} is also regular. - Kleene Closure: If L1 is a regular language, its Kleene closure L1* will also be regular. For example,
L1 = (a ∪ b)
L1* = (a ∪ b)* - Complement: If L(G) is a regular language, its complement L’(G) will also be regular. The complement of a language can be found by subtracting strings which are in L(G) from all possible strings. For example,
L(G) = {an | n > 3}
L’(G) = {an | n <= 3}
Note : Two regular expressions are equivalent if languages generated by them are same. For example, (a+b*)* and (a+b)* generate same language. Every string which is generated by (a+b*)* is also generated by (a+b)* and vice versa.
How to solve problems with regular expressions and regular languages?
Question 1: Which one of the following languages over the alphabet {0,1} is described by the regular expression?
(0+1)*0(0+1)*0(0+1)*
(A) The set of all strings containing the substring 00.
(B) The set of all strings containing at most two 0’s.
(C) The set of all strings containing at least two 0’s.
(D) The set of all strings that begin and end with either 0 or 1.
Solution:
- Option A says that it must have substring 00. 10101 is also a part of the language but does not contain 00 as a substring. So it is not the correct option.
- Option B says that it can have a maximum of two 0’s but 00000 is also a part of the language. So it is not the correct option.
- Option C says that it must contain at least two 0. In a regular expression, two 0 are present. So this is the correct option.
- Option D says that it contains all strings that begin and end with either 0 or 1. But it can generate strings which start with 0 and end with 1 or vice versa as well. So it is not correct.
Question 2: Which of the following languages is generated by given grammar?
S -> aS | bS | ∊
(A) {an bm | n,m ≥ 0}
(B) {w ∈ {a,b}* | w has equal number of a’s and b’s}
(C) {an | n ≥ 0} ∪ {bn | n ≥ 0} ∪ {an bn | n ≥ 0}
(D) {a,b}*
Solution:
- Option (A) says that it will have 0 or more a followed by 0 or more b. But S -> bS => baS => ba is also a part of language. So (A) is not correct.
- Option (B) says that it will have equal no. of a’s and b’s. But S -> bS => b is also a part of the language. So (B) is not correct.
- Option (C) says either it will have 0 or more a’s or 0 or more b’s or a’s followed by b’s. But as shown in option (A), ba is also part of the language. So (C) is not correct.
- Option (D) says it can have any number of a’s and any number of b’s in any order. So (D) is correct.
Designing Finite Automata from Regular Expression
In this article, we will see some popular regular expressions and how we can convert them to finite automata.
- Even number of a’s: The regular expression for the even number of a’s is (b|ab*ab*)*. We can construct a finite automata as shown in Figure 1.
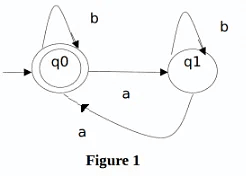 The above automata will accept all strings which have an even number of a’s. For zero a’s, it will be in q0 which is the final state. For one ‘a’, it will go from q0 to q1 and the string will not be accepted. For two a’s at any position, it will go from q0 to q1 for 1st ‘a’ and q1 to q0 for the second ‘a’. So, it will accept all strings with an even number of a’s.
The above automata will accept all strings which have an even number of a’s. For zero a’s, it will be in q0 which is the final state. For one ‘a’, it will go from q0 to q1 and the string will not be accepted. For two a’s at any position, it will go from q0 to q1 for 1st ‘a’ and q1 to q0 for the second ‘a’. So, it will accept all strings with an even number of a’s. - String with ‘ab’ as substring: The regular expression for strings with ‘ab’ as a substring is (a|b)*ab(a|b)*. We can construct finite automata as shown in Figure 2.
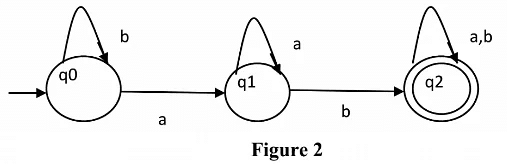 The above automata will accept all strings which have ‘ab’ as substring. The automata will remain in the initial state q0 for b’s. It will move to q1 after reading ‘a’ and remain in the same state for all ‘a’ afterwards. Then it will move to q2 if ‘b’ is read. That means the string has read ‘ab’ as substring if it reaches q2.
The above automata will accept all strings which have ‘ab’ as substring. The automata will remain in the initial state q0 for b’s. It will move to q1 after reading ‘a’ and remain in the same state for all ‘a’ afterwards. Then it will move to q2 if ‘b’ is read. That means the string has read ‘ab’ as substring if it reaches q2. - String with the count of ‘a’ divisible by 3: The regular expression for strings with count of a divisible by 3 is {a3n | n >= 0}. We can construct automata as shown in Figure 3.
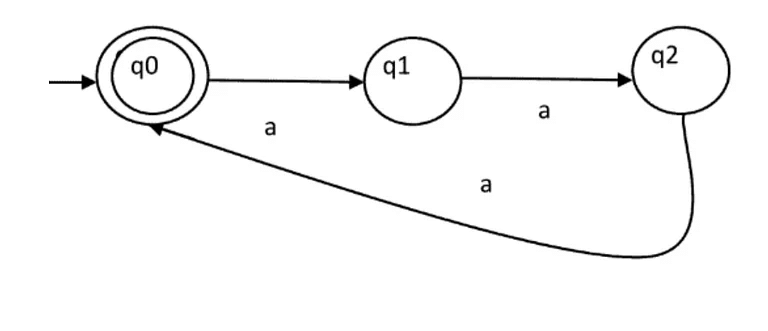 The above automata will accept all strings of form a3n. The automata will remain in the initial state q0 for ɛ and it will be accepted. For string ‘aaa’, it will move from q0 to q1 then q1 to q2 and then q2 to q0. For every set of three a’s, it will come to q0, hence accepted. Otherwise, it will be in q1 or q2, hence rejected.
The above automata will accept all strings of form a3n. The automata will remain in the initial state q0 for ɛ and it will be accepted. For string ‘aaa’, it will move from q0 to q1 then q1 to q2 and then q2 to q0. For every set of three a’s, it will come to q0, hence accepted. Otherwise, it will be in q1 or q2, hence rejected.
Note : If we want to design a finite automata with number of a’s as 3n+1, same automata can be used with final state as q1 instead of q0.
If we want to design a finite automata with language {akn | n >= 0}, k states are required. We have used k = 3 in our example.
- Binary numbers divisible by 3: The regular expression for binary numbers which are divisible by three is (0|1(01*0)*1)*. The examples of binary numbers divisible by 3 are 0, 011, 110, 1001, 1100, 1111, 10010 etc. The DFA corresponding to a binary number divisible by 3 can be shown in Figure 4.
The above automata will accept all binary numbers divisible by 3. For 1001, the automata will go from q0 to q1, then q1 to q2, then q2 to q1 and finally q2 to q0, hence accepted. For 0111, the automata will go from q0 to q0, then q0 to q1, then q1 to q0 and finally q0 to q1, hence rejected.
- String with a regular expression (111 + 11111)*: The string accepted using this regular expression will have 3, 5, 6(111 twice), 8 (11111 once and 111 once), 9 (111 thrice), 10 (11111 twice) and all other counts of 1 afterwards. The DFA corresponding to the given regular expression is given in Figure 5.
Question: What will be the minimum number of states for strings with an odd number of a’s?
Solution: The regular expression for an odd number of a is b*ab*(ab*ab*)* and the corresponding automata is given in Figure 6 and minimum number of states are 2.
Conversion from NFA to DFA
An NFA can have zero, one or more than one move from a given state on a given input symbol. An NFA can also have NULL moves (moves without input symbol). On the other hand, DFA has one and only one move from a given state on a given input symbol.
Suppose there is an NFA N < Q, ∑, q0, δ, F > which recognizes a language L. Then the DFA D < Q’, ∑, q0, δ’, F’ > can be constructed for language L as:
Step 1: Initially Q’ = ɸ.
Step 2: Add q0 to Q’.
Step 3: For each state in Q’, find the possible set of states for each input symbol using the transition function of NFA. If this set of states is not in Q’, add it to Q’.
Step 4: Final state of DFA will be all states which contain F (final states of NFA)
Example: Consider the following NFA shown in Figure 1.
Following are the various parameters for NFA.
Q = { q0, q1, q2 }
∑ = ( a, b )
F = { q2 }
δ (Transition Function of NFA)'
Step 1: Q’ = ɸ
Step 2: Q’ = {q0}
Step 3: For each state in Q’, find the states for each input symbol.
Currently, the state in Q’ is q0, find moves from q0 on input symbols a and b using the transition function of NFA and update the transition table of DFA.
δ’ (Transition Function of DFA)
Now { q0, q1 } will be considered as a single state. As its entry is not in Q’, add it to Q’.
So Q’ = { q0, { q0, q1 } }
Now, moves from state { q0, q1 } on different input symbols are not present in the transition table of DFA, we will calculate it as follows:
δ’ ( { q0, q1 }, a ) = δ ( q0, a ) ∪ δ ( q1, a ) = { q0, q1 }
δ’ ( { q0, q1 }, b ) = δ ( q0, b ) ∪ δ ( q1, b ) = { q0, q2 }
Now we will update the transition table of DFA.
δ’ (Transition Function of DFA)
Now { q0, q2 } will be considered as a single state. As its entry is not in Q’, add it to Q’.
So Q’ = { q0, { q0, q1 }, { q0, q2 } }
Now, moves from state {q0, q2} on different input symbols are not present in the transition table of DFA, we will calculate it as follows:
δ’ ( { q0, q2 }, a ) = δ ( q0, a ) ∪ δ ( q2, a ) = { q0, q1 }
δ’ ( { q0, q2 }, b ) = δ ( q0, b ) ∪ δ ( q2, b ) = { q0 }
Now we will update the transition table of DFA.
δ’ (Transition Function of DFA)
As there is no new state generated, we are done with the conversion. The final state of DFA will be a state which has q2 as its component i.e., { q0, q2 }
Following are the various parameters for DFA.
Q’ = { q0, { q0, q1 }, { q0, q2 } }
∑ = ( a, b )
F = { { q0, q2 } } and transition function δ’ as shown above. The final DFA for the above NFA has been shown in Figure 2.
Note : Sometimes, it is not easy to convert regular expression to DFA. First you can convert regular expression to NFA and then NFA to DFA.
Question: The number of states in the minimal deterministic finite automaton corresponding to the regular expression (0 + 1)* (10) is ____________.
Solution: First, we will make an NFA for the above expression. To make an NFA for (0 + 1)*, NFA will be in same state q0 on input symbol 0 or 1. Then for concatenation, we will add two moves (q0 to q1 for 1 and q1 to q2 for 0) as shown in Figure.
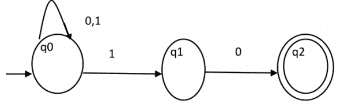
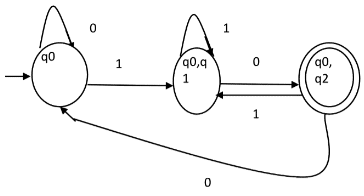
Minimization of DFA
DFA minimization stands for converting a given DFA to its equivalent DFA with minimum number of states.
Suppose there is a DFA D < Q, ∑, q0, δ, F > which recognizes a language L. Then the minimized DFA D < Q’, ∑, q0, δ’, F’ > can be constructed for language L as:
Step 1: We will divide Q (set of states) into two sets. One set will contain all final states and another set will contain non-final states. This partition is called P0.
Step 2: Initialize k = 1
Step 3: Find Pk by partitioning the different sets of Pk-1. In each set of Pk-1, we will take all possible pairs of states. If two states of a set are distinguishable, we will split the sets into different sets in Pk.
Step 4: Stop when Pk = Pk-1 (No change in partition)
Step 5: All states of one set are merged into one. No. of states in minimized DFA will be equal to no. of sets in Pk.
How to find whether two states in partition Pk are distinguishable?
Two states ( qi, qj ) are distinguishable in partition Pk if, for any input symbol a, δ ( qi, a ) and δ ( qj, a ) are in different sets in partition Pk-1.
Example: Consider the following DFA shown in the figure given below:
Step 1. P0 will have two sets of states. One set will contain q1, q2, q4 which are the final states of DFA and another set will contain the remaining states. So P0 = { { q1, q2, q4 }, { q0, q3, q5 } }.
Step 2. To calculate P1, we will check whether sets of partition P0 can be partitioned or not:
For set { q1, q2, q4 } :
δ ( q1, 0 ) = δ ( q2, 0 ) = q2 and δ ( q1, 1 ) = δ ( q2, 1 ) = q5, So q1 and q2 are not distinguishable.
Similarly, δ ( q1, 0 ) = δ ( q4, 0 ) = q2 and δ ( q1, 1 ) = δ ( q4, 1 ) = q5, So q1 and q4 are not distinguishable.
Since q1 and q2 are not distinguishable and q1 and q4 are also not distinguishable, So q2 and q4 are not distinguishable. So, { q1, q2, q4 } set will not be partitioned in P1.
For set { q0, q3, q5 } :
δ ( q0, 0 ) = q3 and δ ( q3, 0 ) = q0
δ ( q0, 1) = q1 and δ ( q3, 1 ) = q4
Moves of q0 and q3 on input symbol 0 are q3 and q0 respectively which are in the same set in partition P0. Similarly, Moves of q0 and q3 on input symbol 1 are q3 and q0 which are in the same set in partition P0. So, q0 and q3 are not distinguishable.
δ ( q0, 0 ) = q3 and δ ( q5, 0 ) = q5 and δ ( q0, 1 ) = q1 and δ ( q5, 1 ) = q5
Moves of q0 and q5 on input symbol 0 are q3 and q5 respectively which are in different set in partition P0. So, q0 and q5 are distinguishable. So, set { q0, q3, q5 } will be partitioned into { q0, q3 } and { q5 }. So,
P1 = { { q1, q2, q4 }, { q0, q3}, { q5 } }
To calculate P2, we will check whether sets of partition P1 can be partitioned or not:
For set { q1, q2, q4 } :
δ ( q1, 0 ) = δ ( q2, 0 ) = q2 and δ ( q1, 1 ) = δ ( q2, 1 ) = q5, So q1 and q2 are not distinguishable.
Similarly, δ ( q1, 0 ) = δ ( q4, 0 ) = q2 and δ ( q1, 1 ) = δ ( q4, 1 ) = q5, So q1 and q4 are not distinguishable.
Since q1 and q2 are not distinguishable and q1 and q4 are also not distinguishable, So q2 and q4 are not distinguishable. So, { q1, q2, q4 } set will not be partitioned in P2.
For set { q0, q3 } :
δ ( q0, 0 ) = q3 and δ ( q3, 0 ) = q0
δ ( q0, 1 ) = q1 and δ ( q3, 1 ) = q4
Moves of q0 and q3 on input symbol 0 are q3 and q0 respectively which are in the same set in partition P1. Similarly, Moves of q0 and q3 on input symbol 1 are q3 and q0 which are in the same set in partition P1. So, q0 and q3 are not distinguishable.
For set { q5 }:
Since we have only one state in this set, it can’t be further partitioned. So,
P2 = { { q1, q2, q4 }, { q0, q3 }, { q5 } }
Since, P1=P2. So, this is the final partition. Partition P2 means that q1, q2 and q4 states are merged into one. Similarly, q0 and q3 are merged into one. Minimized DFA corresponding to DFA of Figure 1 is shown in Figure 2 as:
Question: Consider the given DFA. Which of the following is false?
1. Complement of L(A) is context-free.
2. L(A) = L ( ( 11 * 0 + 0 ) ( 0 + 1 )* 0* 1* )
3. For the language accepted by A, A is the minimal DFA.
4. A accepts all strings over { 0, 1 } of length atleast two.
(A) 1 and 3 only
(B) 2 and 4 only
(C) 2 and 3 only
(D) 3 and 4 only
Solution: Statement 4 says, it will accept all strings of length atleast 2. But it accepts 0 which is of length 1. So, 4 is false.
Statement 3 says that the DFA is minimal. We will check using the algorithm discussed above.
P0 = { { q2 }, { q0, q1 } }
P1 = { q2 }, { q0, q1 } }. Since, P0 = P1, P1 is the final DFA. q0 and q1 can be merged. So minimal DFA will have two states. Therefore, statement 3 is also false.
So correct option is (D).
Chomsky Hierarchy
According to Chomsky hierarchy, grammars are divided of 4 types:
Type 0 known as unrestricted grammar.
Type 1 known as context sensitive grammar.
Type 2 known as context free grammar.
Type 3 Regular Grammar.
Type 0 (Unrestricted Grammar)
In Type 0:
Type-0 grammars include all formal grammars. Type 0 grammar language are recognized by turing machine. These languages are also known as the recursively enumerable languages.
Grammar Production in the form of
α→β
where
α is (V + T)* V (V + T)*
V : Variables
T : Terminals.
β is (V + T)*.
In type 0 there must be at least one variable on Left side of production.
For example,
Sab –> ba
A –> S.
Here, Variables are S, A and Terminals a, b.
Type 1 (Context Sensitive)
Type-1 grammars generate the context-sensitive languages. The language generated by the grammar are recognized by the Liner Bound Automat.
In Type 1:
1. First of all Type 1 grammar should be Type 0.
2. Grammar Production in the form of
α→β
|α| <= |β|
i.e count of symbol in α is less than or equal to β
For Example,
S –> AB
AB –> abc
B –> b
Type 2 (Context Free)
Type-2 grammars generate the context-free languages. The language generated by the grammar is recognized by a Non Deterministic Push down Automata. Type-2 grammars generate the context-free languages.
In Type 2,
1. First of all it should be Type 1.
2. Left hand side of production can have only one variable.
|α| = 1.
Their is no restriction on β.
For example,
S –> AB
A –> a
B –> b
Type 3 (Regular Grammar)
Type-3 grammars generate the regular languages. These languages are exactly all languages that can be decided by a finite state automaton.
Type 3 is most restricted form of grammar.
Type 3 should be in the given form only :
V –> VT* / T*.
(or)
V –> T*V /T*
for example :
S –> ab.
Mealy and Moore Machines
Moore Machines
Moore machines are finite state machines with output value and its output depends only on present state. It can be defined as (Q, q0, ∑, O, δ, λ) where:
- Q is finite set of states.
- q0 is the initial state.
- ∑ is the input alphabet.
- O is the output alphabet.
- δ is transition function which maps Q×∑ → Q.
- λ is the output function which maps Q → O.
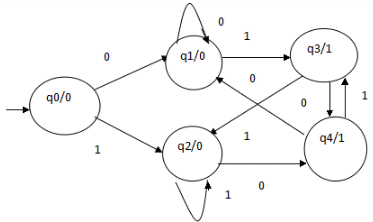
In the moore machine shown in Figure, the output is represented with each input state separated by /. The length of output for a moore machine is greater than input by 1.
- Input: 11
- Transition: δ (q0,11)=> δ(q2,1)=>q2
- Output: 000 (0 for q0, 0 for q2 and again 0 for q2)
Mealy Machines
Mealy machines are also finite state machines with output value and its output depends on present state and current input symbol. It can be defined as (Q, q0, ∑, O, δ, λ’) where:
- Q is finite set of states.
- q0 is the initial state.
- ∑ is the input alphabet.
- O is the output alphabet.
- δ is transition function which maps Q×∑ → Q.
- ‘λ’ is the output function which maps Q×∑→ O.
In the mealy machine shown in Figure , the output is represented with each input symbol for each state separated by /. The length of output for a mealy machine is equal to the length of input.
- Input:11
- Transition: δ (q0,11)=> δ(q2,1)=>q2
- Output: 00 (q0 to q2 transition has Output 0 and q2 to q2 transition also has Output 0)
Conversion from Mealy to Moore Machine
Let us take the transition table of mealy machine shown in Figure above.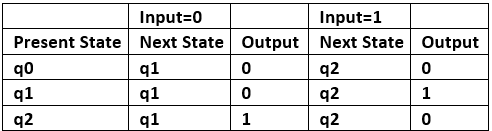
Table 1
Step 1. First find out those states which have more than 1 outputs associated with them. q1 and q2 are the states which have both output 0 and 1 associated with them.
Step 2. Create two states for these states. For q1, two states will be q10 (state with output 0) and q11 (state with output 1). Similarly for q2, two states will be q20 and q21.
Step 3. Create an empty moore machine with new generated state. For moore machine, Output will be associated to each state irrespective of inputs.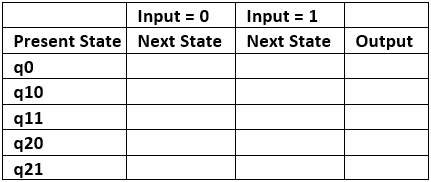
Table 2
Step 4. Fill the entries of next state using mealy machine transition table shown in Table 1. For q0 on input 0, next state is q10 (q1 with output 0). Similarly, for q0 on input 1, next state is q20 (q2 with output 0). For q1 (both q10 and q11) on input 0, next state is q10. Similarly, for q1(both q10 and q11), next state is q21. For q10, output will be 0 and for q11, output will be 1. Similarly, other entries can be filled.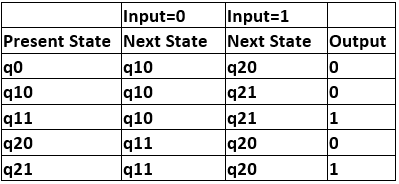
Table 3
This is the transition table of moore machine shown in Figure 1.
Conversion from moore machine to mealy machine
Let us take the moore machine of Figure 1 and its transition table is shown in Table 3.
Step 1. Construct an empty mealy machine using all states of moore machine as shown in Table 4.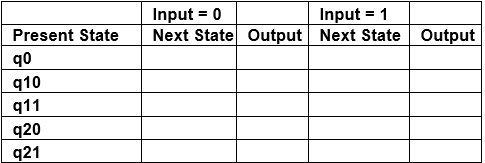
Table 4
Step 2: Next state for each state can also be directly found from moore machine transition Table as: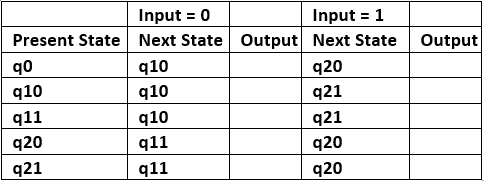
Table 5
Step 3: As we can see output corresponding to each input in moore machine transition table. Use this to fill the Output entries. e.g.; Output corresponding to q10, q11, q20 and q21 are 0, 1, 0 and 1 respectively.
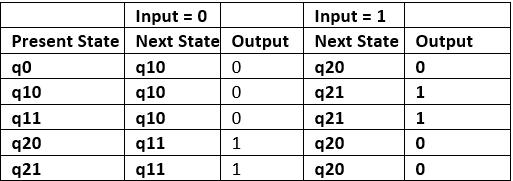
Table 6
Step 4: As we can see from table 6, q10 and q11 are similar to each other (same value of next state and Output for different Input). Similarly, q20 and q21 are also similar. So, q11 and q21 can be eliminated.
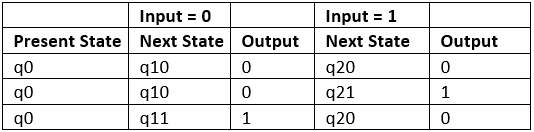
Table 7
This is the same mealy machine shown in Table 1. So we have converted mealy to moore machine and converted back moore to mealy.
Note: Number of states in mealy machine can’t be greater than number of states in moore machine.
Example: The Finite state machine described by the following state diagram with A as starting state, where an arc label is x / y and x stands for 1-bit input and y stands for 2- bit output?
Outputs the sum of the present and the previous bits of the input.
- Outputs 01 whenever the input sequence contains 11.
- Outputs 00 whenever the input sequence contains 10.
- None of these.
Solution: Let us take different inputs and its output and check which option works:
Input: 01
Output: 00 01 (For 0, Output is 00 and state is A. Then, for 1, Output is 01 and state will be B)
Input: 11
Output: 01 10 (For 1, Output is 01 and state is B. Then, for 1, Output is 10 and state is C)
As we can see, it is giving the binary sum of present and previous bit. For first bit, previous bit is taken as 0.
FAQs on Regular Expressions & Finite Automata - GATE Computer Science Engineering(CSE) 2026 Mock Test Series - Computer Science Engineering (CSE)
| 1. What are some important concepts related to Finite Automata and Regular Expressions? |  |
| 2. How can Finite Automata be designed from Regular Expressions? |  |
| 3. What is the process of converting NFA to DFA? |  |
| 4. How can a Deterministic Finite Automaton (DFA) be minimized? |  |
| 5. What is the Chomsky Hierarchy and its relevance to Finite Automata? |  |



















