Resistors in Series and Parallel | Additional Documents & Tests for IIT JAM PDF Download
If two resistors are connected in Figure so that all of the electric charge must traverse both resistors in succession, the equivalent resistance to the flow of current is the sum of the resistances.
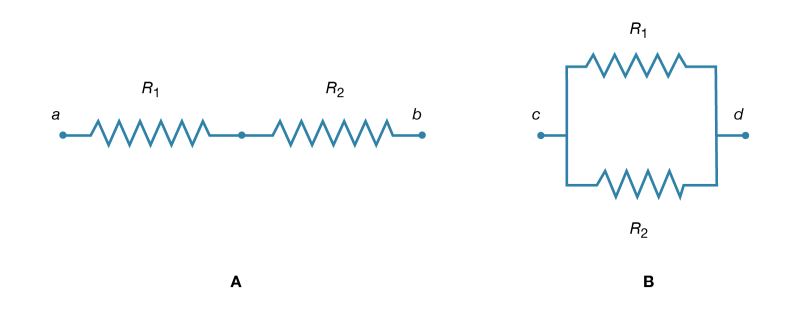
Figure : Resistors. (A) In series. (B) In parallel.
Using R1 and R2 for the individual resistances, the resistance between a and b is given by
Rab =R1+R2 (25a)
This result can be appreciated by thinking of the two resistors as two pieces of the same type of thin wire. Connecting the wires in series as shown simply increases their length to equal the sum of their two lengths. As equation (20) indicates, the resistance is the same as that given by equation (25a). The resistances R1 and R2 can be replaced in a circuit by the equivalent resistance Rab. If R1 = 5Ω and R2 = 2Ω, then Rab = 7Ω. If two resistors are connected as shown in Figure the electric charges have alternate paths for flowing from c to d. The resistance to the flow of charge from c to d is clearly less than if either R1 or R2 were missing. Anyone who has ever had to find a way out of a crowded theatre can appreciate how much easier it is to leave a building with several exits than one with a single exit. The value of the equivalent resistance for two resistors in parallel is given by the equation
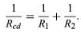 (25a)
(25a)
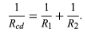 (25b)
(25b)
This relationship follows directly from the definition of resistance in equation (20), where 1/R is proportional to the area. If the resistors R1 and R2 are imagined to be wires of the same length and material, they would be wires with different cross-sectional areas. Connecting them in parallel is equivalent to placing them side by side, increasing the total area available for the flow of charge. Clearly, the equivalent resistance is smaller than the resistance of either resistor individually. As a numerical example, for R1 = 5Ω and R2 = 2Ω, 1/Rcd = 1/5 + 1/2 = 0.7. Therefore, Rcd= 1/0.7 = 1.43Ω. As expected, the equivalent resistance of 1.43 ohms is smaller than either 2 ohms or 5 ohms. It should be noted that both equations (25a) and (25b) are given in a form in which they can be extended easily to any number of resistances.
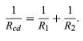 (25b)
(25b)

|
Explore Courses for IIT JAM exam
|

|

















