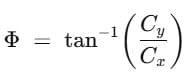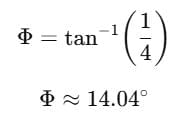Resolution, Addition & Subtraction of Vectors | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Resolution of Vectors |

|
| Addition of Vectors |

|
| Graphical Representation of Vector Addition |

|
| Vector Subtraction |

|
| Properties of Vector Addition |

|
Resolution of Vectors
A vector in a 2-D space can be expressed as the sum of its components along the x and y axes. This is known as resolution of a vector.
- Consider the vector "
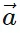 " on an X-Y plane.
" on an X-Y plane. - By drawing and constructing, we form a parallelogram, applying the Parallelogram Law of Vector Addition. This yields two vectors,
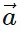 x, and
x, and  y, which are the components of the original vector
y, which are the components of the original vector  .
.
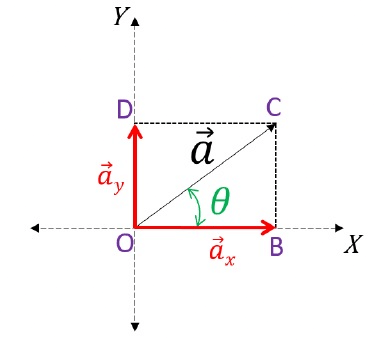 Representing Vector on X-Y Plane
Representing Vector on X-Y Plane
- To find the magnitudes of these components, we use trigonometry. The x-component (
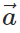 x) is the magnitude of
x) is the magnitude of 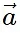 times the cosine of the angle (θ), while the y-component (
times the cosine of the angle (θ), while the y-component (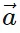 y) is the magnitude of
y) is the magnitude of 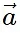 times the sine of θ.
times the sine of θ. - The subtended angle touches one component, and the other is automatically determined.
- In coordinate systems, unit vectors î, ĵ, and k̂ represent X, Y, and Z axes. These unit vectors have a magnitude of 1. Expressing a vector in component form involves multiplying its magnitude by the cosine or sine of the angle, depending on the axis, and then attaching the corresponding unit vector.
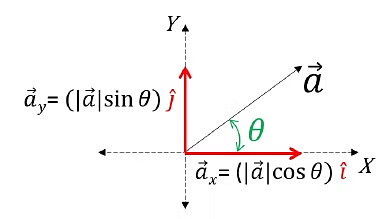 Components of a Vector
Components of a Vector
- In simple terms, a vector a can be expressed as a sum of its x and y components:
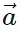 x = |
x = |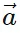 | cos θ î and
| cos θ î and 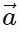 y = |
y = |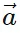 | sin θ ĵ. Therefore,
| sin θ ĵ. Therefore, 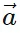 =
= 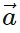 x +
x + 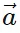 y can be written as (
y can be written as (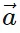 x cos θ ) î + (
x cos θ ) î + (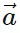 y sin θ ) ĵ in component form.
y sin θ ) ĵ in component form.
Ex 1. A ball is thrown with an initial velocity of 70 feet per second., at an angle of 35° with the horizontal. Find the vertical and horizontal components of the velocity.
Ans. Let v represent the velocity and use the given information to write v in unit vector form:
v =70 cos(35°)î +70 sin(35°)ĵ
Simplify the scalars, we get:
v ≈ 57.34 î + 40.15 ĵ
Since the scalars are the horizontal and vertical components of v,
Therefore, the horizontal component is 57.34 feet per second and the vertical component is 40.15 feet per second.
Rectangular Components of a Vector in 3D
When a vector 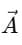 is drawn in 3D space, it can make angles with the X, Y, and Z axes.
is drawn in 3D space, it can make angles with the X, Y, and Z axes.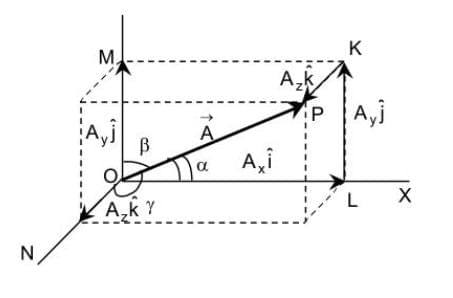
- Let these angles be α, β, γ.
- The vector is written as:
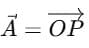
Components of the Vector
The vector 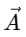 can be split into three parts:
can be split into three parts:
Along X-axis:
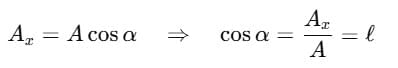
Along Y-axis:

Along Z-axis:
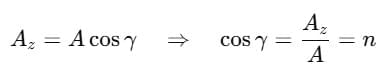
So,
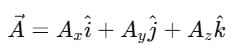
Magnitude of the Vector
Using Pythagoras' theorem in 3D: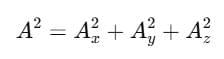
So, 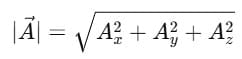
This gives the length (magnitude) of the vector.
Direction Cosines
The values cosα, cosβ, cosγ are called the direction cosines of the vector 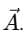 They tell us how much the vector is inclined towards each axis.
They tell us how much the vector is inclined towards each axis.
A very important result is:
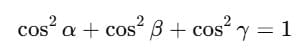
Or, in terms of ℓ, m, n:
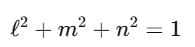
Addition of Vectors
In vectors, both magnitude and direction matter, therefore, the process of addition differs from simple algebraic addition.
Here are some crucial points regarding vector addition:
- The addition or composition of vectors means finding the resultant of many vectors acting on a body.
- Geometric Addition: Vectors are combined geometrically, considering both magnitude and direction.
- Independence: Vectors undergoing addition behave independently of each other as if the presence of one does not affect the behavior of the other.
Ex 2. Find the addition of vectors PQ and QR, where PQ = (3, 4) and QR = (2, 6).
Ans. We will perform the vector addition by adding their corresponding components
PQ + QR = (3, 4) + (2, 6)
= (3 + 2, 4 + 6)
= (5, 10).
Graphical Representation of Vector Addition
To visualize the sum of vectors a and b (i.e., a + b), one can shift vector b so that its initial point coincides with the terminal point of vector a. The resulting vector, starting from the initial point of a to the terminal point of b, represents the sum a + b.
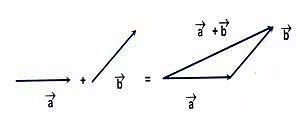 Graphical Representation of Vector Addition
Graphical Representation of Vector Addition
1. Triangle’s Law of Vector Addition
It states that if two vectors A and B are represented by two sides of a triangle, taken in the same order, then their resultant is represented by the third side of the triangle, taken in the opposite order. Mathematically, this is expressed as A + B = C.
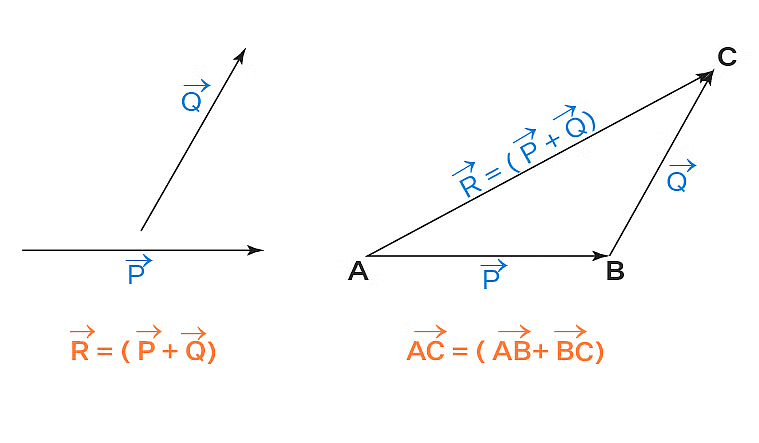 Triangle Law of Vector Addition
Triangle Law of Vector Addition
2. Parallelogram Addition of Vectors
It states that if two vectors P and Q are represented by two adjacent sides of a parallelogram, both pointing outwards, then their resultant is given by the diagonal drawn through the intersection of the two vectors.
- The magnitude and direction of the resultant can be calculated using specific formulas.
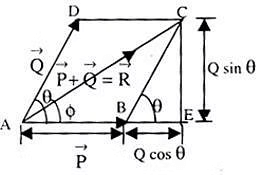 Parallelogram Addition of Vectors
Parallelogram Addition of Vectors - When combining two vectors using the parallelogram method, the magnitude of the resulting vector (R) is determined by the formula: (AC)2 = (AE)2 + (EC)2
or R2 = (P + Q cos θ)2 + (Q sin θ)2
or R = √(P2+ Q2 )+ 2PQcos θ - This formula essentially relates the lengths of the vectors involved (P and Q) and the angle (θ) between them.
- The direction of the resulting vector, relative to vector P, is given by:
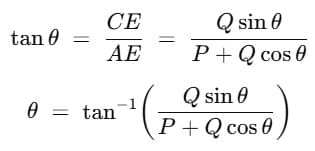
Special Cases in Vector Addition
(a) When θ = 0°, cos θ = 1, sin θ = 0°
Substituting for cos θ in equation R = √(P2+ Q2 )+ 2PQcos θ, we get,
R = √(P2+ Q2 )+ 2PQcos θ
= √(P+ Q)2
or R = P+Q (maximum)
Substituting for sin θ and cos θ in equation 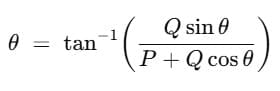 , we get,
, we get,
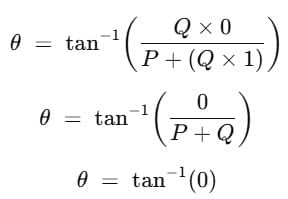
= 0°
The resultant of two vectors acting in the same direction is equal to the sum of the two. The direction of the resultant coincides with those of the two vectors.
(b) When θ = 180°, cos θ = -1, sin θ = 0°
Substituting for cos θ in equation R = √(P2+ Q2 )+ 2PQcos θ, we get,
R = √(P2+ Q2 )+ 2PQ(-1)
=√P2+ Q2 – 2PQ
= √(P – Q)2 (minimum)
or R = P – Q (minimum)
Substituting for sin θ and cos θ in equation 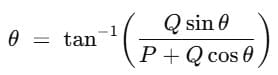 , we get,
, we get,
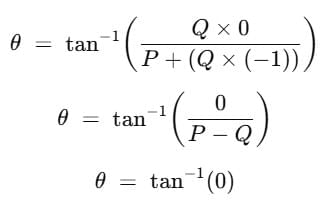
= 0°
This magnitude of the resultant of two vectors acting in opposite directions is equal to the difference in magnitudes of the two and represents the minimum value. The direction of the resultant is in the direction of the bigger one.
(c) When θ = 90°, cos θ = 0 , sin θ = 1
Substituting for cos θ in equation R = √(P2+ Q2 )+ 2PQcos θ, we get,
R = √(P2+ Q2 )+ (2PQ×0)
= √P2+ Q2
Substituting for sin θ and cos θ in equation 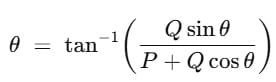 , we get,
, we get,
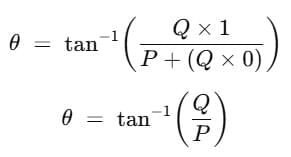
The resultant of two vectors acting at right angles to each other is equal to the square root of the sum of the squares of the magnitudes of the two vectors. The direction of the resultant depends upon their relative magnitudes.
Ex 3. Two vectors are given along with their components: A = (2,3) and B = (2,-2). Calculate the magnitude and the angle of the sum C using their components.
Ans. Let us represent the components of the given vectors as: In the vector A, Ax = 2 and Ay= 3In the vector B, Bx = 2 and By = -2
Now, adding the two vectors,
A + B = (2, 3) + (2, -2) = (4, 1)
It can also be written as:
C = (4, 1)
Here in C, Cx = 4 and Cy = 1
The magnitude of the resultant vector C can be calculated as:The angle can be calculated as follows:
Vector Subtraction
Vector subtraction is a process equivalent to adding the negative of the vector to be subtracted. For instance, if subtracting vector B from vector A, it is essentially the same as adding -B to A.
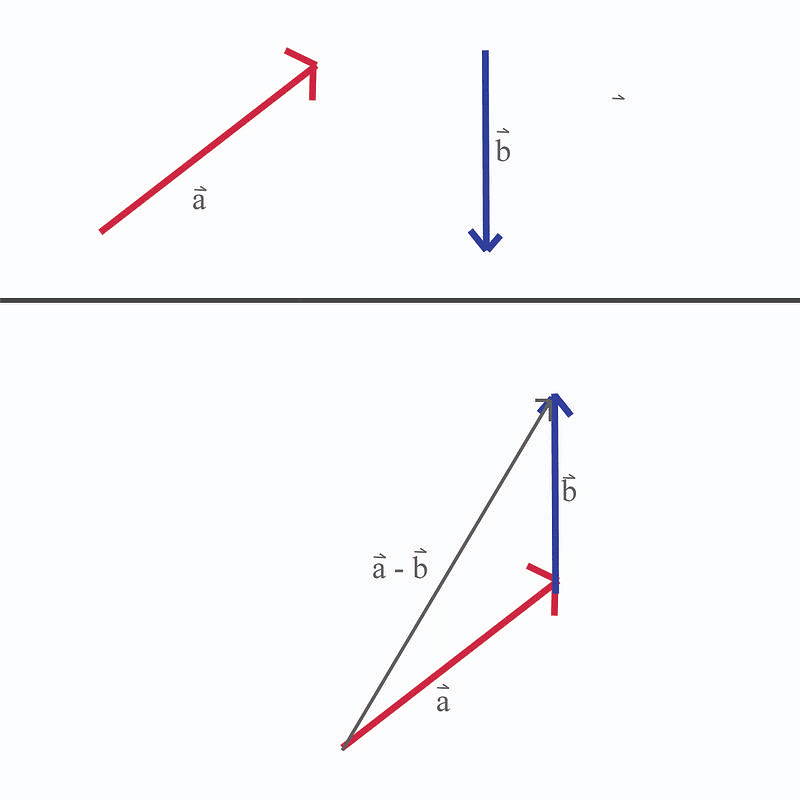 Vector Subtraction
Vector Subtraction
Properties of Vector Addition
The properties of vector addition further enhance its utility:
- Commutative: The order of vectors in addition does not influence the result, showcasing the commutative property.
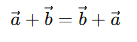
- Associative: While adding three or more vectors, the grouping of vectors does not affect the result, demonstrating the associative property.
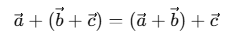
- Distributive: Scalar multiplication distributes over vector addition, offering a convenient mathematical feature.
These properties make vector addition a versatile and powerful operation, applicable in various mathematical and physical scenarios.
|
268 videos|780 docs|209 tests
|
FAQs on Resolution, Addition & Subtraction of Vectors - Physics for JEE Main & Advanced
| 1. What is the graphical method of vector addition? |  |
| 2. How do you resolve a vector into its components? |  |
| 3. What are the special cases in vector addition? |  |
| 4. How is vector subtraction performed? |  |
| 5. What are the properties of vector addition? |  |