Chemical Thermodynamics Class 11 Notes Chemistry Chapter 5
Basic Terminology
Terms | Explanation |
System | Part of the universe under investigation. |
Open System | A system which can exchange both energy and matter with its surroundings. |
Closed System | A system which permits passage of energy but not mass, across its boundary. |
Isolated system | A system which can neither exchange energy nor matter with its surrounding. |
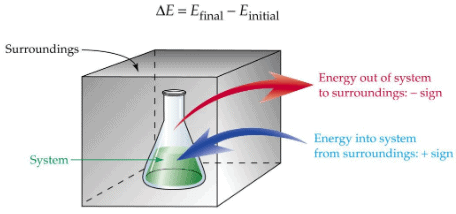
Surroundings | Part of the universe other than system, which can interact with it. |
Boundary | Anything which separates system from surrounding. |
State variables | The variables which are required to be defined in order to define state of any system i.e. pressure, volume, mass, temperature, surface area, etc. |
State Functions | Property of system which depend only on the state of the system and not on the path. |
Example: Pressure, volume, temperature, internal energy, enthalpy, entropy etc. | |
Intensive properties | Properties of a system which do not depend on mass of the system i.e. temperature, pressure, density, concentration, |
Extensive properties | Properties of a system which depend on mass of the system i.e. volume, energy, enthalpy, entropy etc. |
Process | Path along which state of a system changes. |
Isothermal process | Process which takes place at constant temperature |
Isobaric process | Process which takes place at constant pressure |
Isochoric process | Process which takes place at constant volume. |
Adiabatic process | Process during which transfer of heat cannot take place between system and surrounding. |
Cyclic process | Process in which system comes back to its initial state after undergoing series of changes. |
Reversible process | Process during which the system always departs infinitesimally from the state of equilibrium i.e. its direction can be reversed at any moment. |
Irriversible Process | This type of process is fast and gets completed in a single step. This process cannot be reversed. All the natural processes are of this type |
HEAT, ENERGY AND WORK
HEAT (Q):
- Energy is exchanged between system and surround in the form of heat when they are at different temperatures.
- Heat added to a system is given by a positive sign, whereas heat extracted from a system is given negative sign.
- It is an extensive property.
- It is not a state function.
ENERGY:
- It is the capacity for doing work.
- Energy is an extensive property.
- Unit : Joule.
Work (W):
- Work = Force × Displacement i.e. dW = Fdx
- Work done on the system is given by positive sigh while work done by the system is given negative sign.
- Mechanical Work or Pressure-Volume Work: work associated with change in volume of a system against an external pressure.
- Work done in reversible process: W=

W = – 2.303 nRT log v2/v1 = –2.303 nRT log p1/p2 - Wok done in isothermal reversible contraction of an ideal gas:
?W = – 2.303 nRT log v2/v1 = –2.303 nRT log p1/p2 - Unit : Joule.
Internal Energy (E or U):
- Sum of all the possible types of energy present in the system.
- ΔE = heat change for a reaction taking place at constant temperature and volume.
- ΔE is a state function.
- It is an extensive property.
- Value of ΔE is -ve for exothermic reactions while it is +ve for endothermic reactions.

First Law of Thermodynamics:
Energy can neither be created nor destroyed although it can be converted from one form to another.
or
Energy of an isolated system is constant.
Mathematical Expression
Heat observed by the system = its internal energy + work done by the system.
i.e. q = dE + w
For an infinitesimal process
dq = dE + dw
Where, q is the heat supplied to the system and w is the work done on the system.
For an ideal gas undergoing isothermal change ΔE =0.
so q= -w.
For an isolated system, dq=0
so, dE = - dw
For system involving mechanical work only
ΔE = q - pdV
At constant volume i.e. isochoric process
ΔE = qv
For Isothermal Process
ΔE = 0
or
q = - pdV =-W
For adiabatic process
?q = 0
or
ΔE = W
Enthalpy (H):
H = E+PV
At constant pressure:
dH = dE + pdV
For system involving mechanical work only
dH = QP (At constant pressure)
For exothermic reactions:
dH = -ve
For endothermic reactions:
dH = +ve
Relation between dH and dE:
dH = dE + dng RT
Where,
dng = (Number of moles of gaseous products - Number of moles of gaseous reactants)
Heat capacity:
Amount of heat required to rise temperature of the system by one degree.
C = q / dT
Specific heat capacity: Heat required to raise the temperature of 1 g of a substance by one degree.
Cs = Heat capacity / Mass in grams
Molar heat capacity: Heat required to raise the temperature of 1 g of a substance by one degree.
Cm = Heat capacity / Molar mass.
Heat capacity of system at constant volume:
Cv = (dE/dT)v
Heat capacity of system at constant pressure:
Cp = (dE/dT)pCp – Cv = R
Variation Of Heat Of Reaction With Temperature:dCP = (dH2 - dH1)/(T2-T1) & dCV = (dE2 - dE1)/(T2-T1
Bomb Calorimeter
Heat exchange = Z × Δ
Z–Heat capacity of calorimeter system
ΔT– Rise in temp.
Heat changes at constant volumes are expressed in ΔE and Heat changes at constant
pressure are expressed in dH.
ENTHALPIES OF REACTIONS
(i) Enthalpy of Formation
- Definitions - Enthalpy change when one mole of a given compound is formed from its elements
- Example - H2(g) + 1/2O2(g) → 2H2O(l), ΔfH = –890.36 kJ / mol
(ii) Enthalpy of Combustion
- Definitions - Enthalpy change when one mole of a substance is burnt in oxygen.
- Example - CH4 + 2O2(g) →CO2 + 2H2O(l), ΔcombH = –890.36 kJ / mol
(iii) Enthalpy of Neutralization
- Definitions - Enthalpy change when one equivalent of an acid is neutralized by a base in dilute solution.
- Example - H+ (aq) + OH– (aq) → H2O(l) ΔneutH = –13.7 kcal
(iv) Enthalpy of Hydration
- Definitions - Enthalpy change when a salt combines with the required number of moles of water to form specific hydrate.
- Example - CuSO4(s) + 5H2O (l) → CuSO45H2O, ΔhydH° = –18.69 kcal
(v) Enthalpy of Transition
- Definitions - Enthalpy change when one mole of a substance is transformed from one allotropic form to another allotropic form.
- Example - C (graphite) → C(diamond), ΔtransH° = 1.9 kJ/mol
(vi) Enthalpy of Sublimation
- Definitions - Enthalpy change when one mole of a solid substance sublime at constant temp. and 1 bar pressure
- Example - CO2(S) → CO2(g) ΔtfusH° = 6.00 kJ/mol
(vii) Enthalpy of fusion
- Definitions - Enthalpy change when one mole of a solid melts
- Example - H2O(S) → H2O (l) ΔtsubH° = 73.00 kJ/mol
Hess’s Law of constant heat summation:
The total enthalpy change of a reaction is the same, regardless of whether the reaction is completed in one step or in several steps. According to Hess’s law: ΔH = ΔH1 + ΔH2
According to Hess’s law: ΔH = ΔH1 + ΔH2
Born–Haber Cycle: Applying Hess’s law we get
Applying Hess’s law we get
ΔH1 + 1/2 ΔH2 + ΔH3 + ΔH4 + ΔH5 = ΔHf (MX) (Lattice energy)
Lattice energy: The change in enthalpy that occurs when 1 mole of a solid crystalline substance is formed from its gaseous ions.
SECOND LAW OF THERMODYNAMICS
Statement:
It is impossible to take heat from a hot reservoir and convert it completely into work by a cyclic process without transferring a part of it to a cold reservoirs.
Mathematically:
ΔS = qrev/T
Where,
ΔS is entropy change.
Entropy is the degree of randomness thus it increases with increase in randomness of particles of the system i.e. ΔS is positive for melting of ice.
At equilibrium, ΔS = 0
For a spontaneous process, ΔS > 0
Entropy change in an isothermal reversible expansion of a gas
Spontaneous Processes: These type of physical and chemical changes occur of its own under specific circumstances or on proper initiations. For example: Flow of liquids from higher to lower level.
Gibbs free energy(ΔG):
ΔG = ΔH - TΔS
ΔG = nRT ln Keq
ΔG = nFEcell
At equilibrium, ΔG = 0
For spontaneous process, ΔG < 0
Bond Energies:
Average amount of energy required to break one mole bonds of that type in gaseous molecules.
H–OH(g) → 2H(g) + ½O(g)
ΔH = 498 kJ
O–H(g) → H2(g) + ½O2 (g)
ΔH = 430 Kj
ΔHO–H = (498 + 430)/2 = 464 kJ mol–1
Efficiency of a heat engine (carnot cycle):
W = R (T2 – T1) ln v2/v1
q2 = RT2 ln v2/v1
W = q2
Efficiency (h). h =
|
357 docs|148 tests
|
FAQs on Chemical Thermodynamics Class 11 Notes Chemistry Chapter 5
| 1. What is chemical thermodynamics? |  |
| 2. How is thermodynamics applied in chemistry? |  |
| 3. What are the laws of thermodynamics? |  |
| 4. What is the difference between exothermic and endothermic reactions? |  |
| 5. How does Gibbs free energy relate to chemical reactions? |  |

|
Explore Courses for JEE exam
|

|