JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2025 > Revision Notes - Continuity
Continuity & Differentiability Class 12 Notes Maths Chapter 5
- A function f(x) is said to be continuous at x= a if
limx→a- f(x)= limx→a+ f(x)=f(a)
Thus, unlike limits, for continuity it is essential for the function to be defined at that particular point and the limiting value of the function should be equal to f(a). - The function f(x) will be discontinuous at x =a in either of the following situations:
1. limx→a- f(x) and limx→a+ f(x) exist but are not equal.
2. limx→a- f(x) and limx→a+ f(x) exist and are equal but not equal to f(a).
3. f(a) is not defined.
4. At least one of the limits does not exist. - If you are required to comment on the continuity of a function, then you may just look for the points on the domain where the function is not defined.
Some important properties of continuous functions:
If the functions f(x) and g(x) are both continuous at x =a then the following results hold true:
1. cf (x) is continuous at x =a where c is any constant.
2. f(x) + g(x) is continuous at x = a.
3. f(x).g(x) is continuous at x= a.
4. f(x)/g(x) is continuous at x= a, provided g(a) ≠ 0.
- If a function f is continuous in (a, b), it means it is continuous at every point of (a, b).
- If f is continuous in [a, b] then in addition to being continuous ay every point of domain, f should also be continuous at the end points i.e. f(x) is said to be continuous in the closed interval [a, b] if
1. f(x) is continuous in (a, b)
2. limx→a+ f(x)=f(a)
limx→a- f(x)=f(a) - While solving problems on continuity, one need not calculate continuity at every point, in fact the elementary knowledge of the function should be used to search the points of discontinuity.
- In questions like this where a function h is defined as

h(x) = f(x) for a < x < b
g(x) for b < x < c
The functions f and g are continuous in their respective intervals, then the continuity of function h should be checked only at the point x = b as this is the only possible point of discontinuity. - If the point ‘a’ is finite, then the necessary and sufficient condition for the function f to be continuous at a is that limx→a- f(x) and limn→a+ f(x) should exist and be equal to f(a).
- A function continuous on a closed interval [a, b] is necessarily bounded if both a and b are finite. This is not true in case of open interval.
- If the function u = f(x) is continuous at the point x=a, and the function y=g(u) is continuous at the point u = f(a), then the composite function y=(gof)(x)=g(f(x)) is continuous at the point x=a.
- Given below is the table of some common functions along with the intervals in which they are continuous:Functions f(x)Interval in which f(x) is continuousConstant C(-∞,∞)bn, n is an integer > 0(-∞,∞)|x-a|(-∞,∞)x-n, n is a positive integer.(-∞,∞)-{0}a0xn + a1xn-1 +........ + an-1x + an(-∞,∞)p(x)/q(x), p(x) and q(x) are polynomials in xR - {x:q(x)=0}sin xRcos xRtan xR-{nπ:n=0,±1,........}cot xR-{(2n-1)π/2:n=0,±1,± 2,........}sec xR-{(2n-1)π/2:n=0,±1,± 2,........}exRln x(0, ∞)
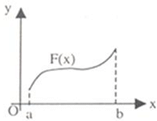
If you know the graph of a function, it can be easily judged without even solving whether a function is continuous or not. The graph below clearly shows that the function is discontinuous.
- If limx→a- f(x) = L1 and limx→a+ f(x) = L2, where L1 and L2 are both finite numbers then it is called discontinuity of first kind or ordinary discontinuity.

- A function is said to have discontinuity of second kindif neither limx→a+ f(x) nor limx→a- f(x) exist.
- If any one of limx→a+ f(x) or limx→a- f(x) exists and the other does not then the function f is said to have mixed discontinuity.
- If limx→a f(x) exists but is not equal to f(a), then f(x) has removable discontinuity at x = a and it can be removed by redefining f(x) at x=a.
- If limx→a f(x) does not exist, then we can remove this discontinuity so that it becomes a non-removable or essential discontinuity.
- A function f(x) is said to have a jump discontinuity at a point x=a if, limx→a-f(x) ≠ limx→a+ f(x) and f(x) and may be equal to either of previous limits.
The concepts of limit and continuity are closely related. Whether a function is continuous or not can be determined by the limit of the function.
The document Continuity & Differentiability Class 12 Notes Maths Chapter 5 is a part of the JEE Course Mock Tests for JEE Main and Advanced 2025.
All you need of JEE at this link: JEE
|
357 docs|148 tests
|
FAQs on Continuity & Differentiability Class 12 Notes Maths Chapter 5
| 1. What is continuity in mathematics? |  |
Ans. Continuity in mathematics refers to the property of a function being unbroken or smooth over its entire domain. It means that there are no sudden jumps, holes, or breaks in the graph of the function.
| 2. How is continuity of a function determined? |  |
Ans. The continuity of a function can be determined by checking three conditions:
1) The function is defined at the point in question.
2) The limit of the function exists at that point.
3) The limit of the function at that point is equal to the value of the function at that point.
| 3. Can a function be continuous at one point but not at others? |  |
Ans. Yes, it is possible for a function to be continuous at one point but not at others. Continuity is a local property, meaning it is determined by the behavior of the function in the immediate neighborhood of a point. A function can have different properties at different points.
| 4. What is the difference between continuity and differentiability? |  |
Ans. Continuity and differentiability are related concepts but not the same. Continuity refers to the smoothness and unbrokenness of a function over its entire domain, while differentiability refers to the ability to find the derivative of a function at a given point. A function can be continuous but not differentiable, but if a function is differentiable, then it must also be continuous.
| 5. Can a function be continuous but not have a derivative? |  |
Ans. Yes, it is possible for a function to be continuous but not have a derivative. Such functions are called "non-differentiable" functions. These functions may have sharp corners, cusps, or vertical tangent lines, which prevent the existence of a derivative.
Related Searches