Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Revision Notes: Coordinate Geometry
Revision Notes: Coordinate Geometry | Mathematics Class 9 ICSE PDF Download
Co-ordinate Geometry is the branch of mathematics in which algebraic methods are used to solve geometrical problems.
Cartesian Plane
- Two perpendicular number lines intersecting at point zero are called coordinate axes. The horizontal number line is the x-axis (denoted by X’OX) and the vertical one is the y-axis (denoted by Y’OY). The point of intersection of x-axis and y-axis is called origin and denoted by ‘O’.
- Cartesian plane is a plane obtained by putting the coordinate axes perpendicular to each other in the plane. It is also called coordinate plane or xy plane.
- The x-coordinate of a point is its perpendicular distance from y-axis.
The y-coordinate of a point is its perpendicular distance from x-axis. - The point where the x axis and the y axis intersect is represented by coordinate points (0, 0) and is called the origin.
- The abscissa of a point is the x-coordinate of the point. The ordinate of a point is the y-coordinate of the point.
- If the abscissa of a point is x and the ordinate of the point is y, then (x, y) are called the coordinates of the point.
- The axes divide the Cartesian plane into four parts called the quadrants (one fourth part), numbered I, II, III and IV anticlockwise from OX.
- Sign of coordinates depicts the quadrant in which it lies.
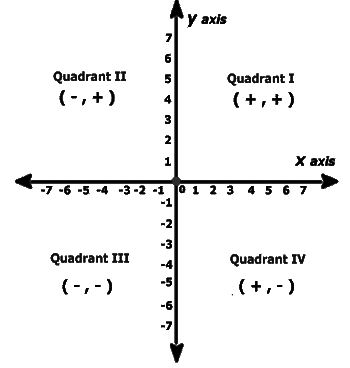
- The coordinates of a point on the x-axis are of the form (x, 0) and that of the point on y-axis are (0, y).
- To plot a point P (3, 4) in the Cartesian plane, start from origin and count 3 units on the positive x axis then move 4 units towards positive y axis. The point at which we will arrive will be the point P (3, 4).
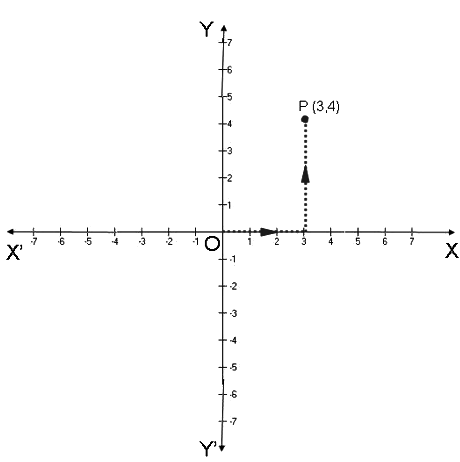
- If x ≠ y, then (x, y) ≠ (y, x) and if (x, y) = (y, x), then x = y.
Graphing a Linear Equation
- The Cartesian plane can be used to graph different kinds of situations from everyday life.
- A line graph which is a whole unbroken line is called a linear graph.
- Two quantities which vary directly can be plotted as a linear graph. Independent variable is generally taken on x axis the dependent variable is taken on y axis.
- Steps to draw a graph:
(i) Find out the relation between y and x.
(ii) Calculate different values of y corresponding to the values of x.
(iii) Tabulate the results.
(iv) Plot the points.
(v) Join the points to obtain the graph. - By looking at a linear graph, we can find out the ‘y’ coordinate (or 'x' coordinate) in relation to any point on the ‘x’ axis (or 'y' axis).
- x = 0 is the equation of the y-axis and y = 0 is the equation of the x-axis.
Inclination and Slope
- The angle which a straight line makes with the positive direction of the x-axis (measured in the anticlockwise direction) is called inclination of the line.
The inclination of the line is usually denoted by θ (theta).
In the below figure, θ = 45°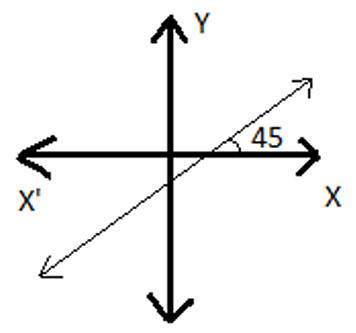
- If θ is the inclination of a line then slope of the line is tan θ and is usually denoted by letter m.
Slope = m = tan θ.
For x-axis and every line parallel to x-axis, the inclination θ = 0°.
Hence, Slope (m) = tan θ = tan 0° = 0
For y-axis and every line parallel to y-axis, the inclination θ = 90°.
Hence, Slope (m) = tan θ = tan 90° = not defined
Y-Intercept
If a straight line meets y-axis at a point, the distance of this point from the origin is called y-intercept and is usually denoted by the letter c.
For x-axis, y-intercept = 0
For every, line parallel to y-axis, y-intercept = 0.
Y-intercept is positive if measure above the origin and negative if measured below the origin.
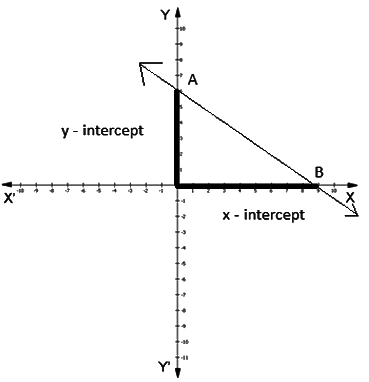 Steps to find Slope and the Y-Intercept of a given line (ax + by + c = 0):
Steps to find Slope and the Y-Intercept of a given line (ax + by + c = 0):- Make y, the subject of the equation.
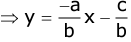
- The coefficient of x is the slope.
⇒ slope (m) = (-a)/b - The constant term is the y-intercept of the given line.
⇒ y - intercept = (-c)/b
The document Revision Notes: Coordinate Geometry | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
64 videos|165 docs|28 tests
|
FAQs on Revision Notes: Coordinate Geometry - Mathematics Class 9 ICSE
| 1. What is coordinate geometry and why is it important in Class 9 mathematics? |  |
Ans. Coordinate geometry, also known as analytic geometry, is a branch of mathematics that uses a coordinate system to study geometric shapes and their properties. In Class 9, it is important because it helps students understand how to represent geometric figures on a Cartesian plane, analyze geometric relationships, and solve problems involving distance, midpoints, and slopes. This foundational knowledge is essential for higher-level mathematics and real-world applications.
| 2. How do you find the distance between two points in a coordinate plane? |  |
Ans. The distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) in a coordinate plane can be found using the distance formula:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
This formula derives from the Pythagorean theorem and allows us to calculate the straight-line distance between any two points.
| 3. What is the midpoint formula and how is it used? |  |
Ans. The midpoint of a line segment defined by two endpoints \( (x_1, y_1) \) and \( (x_2, y_2) \) can be calculated using the midpoint formula:
\[ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]
This formula gives the coordinates of the point that is exactly halfway between the two endpoints, which is useful in various geometric problems.
| 4. Can you explain how to determine the slope of a line given two points? |  |
Ans. The slope of a line passing through two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is calculated using the slope formula:
\[ m = \frac{y_2 - y_1}{x_2 - x_1} \]
The slope \( m \) represents the rate of change of \( y \) with respect to \( x \) and indicates whether the line is rising, falling, or horizontal.
| 5. What are the different types of slopes and what do they represent? |  |
Ans. There are three types of slopes for lines in a coordinate plane:
1. Positive slope: The line rises from left to right, indicating a direct relationship between \( x \) and \( y \).
2. Negative slope: The line falls from left to right, indicating an inverse relationship.
3. Zero slope: The line is horizontal, indicating that \( y \) does not change as \( x \) changes.
These slopes help in understanding the behavior of linear equations and graphs.
Related Searches




















