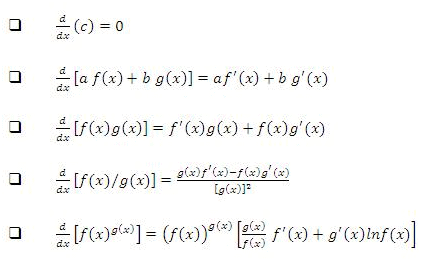JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2025 > Revision Notes - Differentiability
Differentiability Class 11 Notes Maths
- The derivative of f, denoted by f'(x) is given by f'(x) = lim?x→0 (? y)/(? x) = dy/dx
- The right hand derivative of f at x = a is denoted by f'(a+) and is given by f'(a+) = limh→0+(f(a+h)-f(a))/h
- The left hand derivative of f at x = a is denoted by f'(a-) and is given by f'(a-) = limh→0- (f(a-h)-f(a))/-h
- For a function to be differentiable at x=a, we should have f'(a-)=f'(a+) i.e. limh→0 (f (a-h)-f (a))/ (-h) = limh→0 (f (a+h)-f (a))/h.
- limh→0 sin 1/h fluctuates between -1 and 1.
- If at a particular point say x =a, we have f'(a+) = t1 (a finite number) and f'(a-) = t2 (a finite number) and if t1 ≠ t2, then f' (a) does not exist, but f(x) is a continuous function at x = a.
- Continuity and differentiability are quite interrelated.
Differentiability alwaysimpliescontinuity but the converse is not true. This means that a differentiable function is always continuous but if a function is continuous it may or may not be differentiable.
Some basic formulae:
- If a function is not derivable at a point, it need not imply that it is discontinuous at that point. But, however, discontinuity at a point necessarily implies non-derivability.
- In case, a function is not differentiable but is continuous at a particular point say x = a, then it geometrically implies a sharp corner at x = a.
- A function f is said to be derivable over a closed interval [a, b] if :
1. For the points a and b, f'(a+) and f'(b-) exist and
2. For ant point c such that a < c < b, f'(c+)and f'(c-) exist and are equal. - If y = f(u) and u = g(x), then dy/dx = dy/du.du/dx = f'(g(x)) g'(x). This method is also termed as the chain rule.
- For composite functions, differentiation is carried out in this way:
If y = [f(x)]n, then we put u = f(x). So that y = un. Then by chain rule:
dy/dx = dy/du.du/dx = nu(n-1)f' (x) = [f(x)](n-1) f' (x) - Differential calculus problems involving parametric functions:
If x and y are functions of parameter t, first find dx/dt and dy/dt separately. Then dy/dx=(dy/dt)/(dx/dt). - If the functions f(x) and g(x) are derivable at x = a, then the following functions are also derivable:
1.f(x) + g(x)
2.f(x) - g(x)
3.f(x) . g(x)
4.f(x) / g(x), provided g(a) ≠ 0 - If the function f(x) is differentiable at x =a while g(x) is not derivable at x = a, then the product function f(x). g(x) can still be differentiable at x = a.
- Even if both the functions f(x) and g(x) are not differentiable at x = a, the product function f(x).g(x) can still be differentiable at x = a.
- Even if both the functions f(x) and g(x) are not derivable at x = a, the sum function f(x) + g(x) can still be differentiable at x = a.
If function f(x) is derivable at x = a, this need not imply that f'(x) is continuous at x = a.
The document Differentiability Class 11 Notes Maths is a part of the JEE Course Mock Tests for JEE Main and Advanced 2025.
All you need of JEE at this link: JEE
|
357 docs|148 tests
|
FAQs on Differentiability Class 11 Notes Maths
| 1. What is the definition of differentiability? |  |
Ans. Differentiability is a property of a function that measures how smooth and well-behaved it is. A function is said to be differentiable at a point if its derivative exists at that point. The derivative represents the rate of change of the function at that point.
| 2. How is differentiability related to continuity? | |
Ans. Differentiability is a stronger condition than continuity. While all differentiable functions are continuous, not all continuous functions are differentiable. A function is differentiable if and only if it is continuous and its derivative exists at every point in its domain.
| 3. Can a function be differentiable at one point but not at another? | |
Ans. Yes, it is possible for a function to be differentiable at one point but not at another. Differentiability is a local property, meaning it is determined at each individual point. A function may have points where it is differentiable and points where it is not.
| 4. What is the significance of differentiability in calculus? | |
Ans. Differentiability plays a crucial role in calculus as it allows us to determine important properties of functions, such as their rate of change, slope, and optimization. It enables us to find tangent lines, calculate derivatives, and solve optimization problems, making it a fundamental concept in calculus.
| 5. How can I determine if a function is differentiable? | |
Ans. To determine if a function is differentiable at a point, you need to check if its derivative exists at that point. The derivative can be calculated using various methods such as the limit definition of the derivative or using differentiation rules. If the derivative exists, the function is differentiable at that point.
About this Document
|
4.70/5 Rating |
|
Nov 24, 2024 Last updated |
Document Description: Revision Notes - Differentiability for JEE 2024 is part of Mock Tests for JEE Main and Advanced 2025 preparation.
The notes and questions for Revision Notes - Differentiability have been prepared according to the JEE exam syllabus. Information about Revision Notes - Differentiability covers topics
like and Revision Notes - Differentiability Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes - Differentiability.
Introduction of Revision Notes - Differentiability in English is available as part of our Mock Tests for JEE Main and Advanced 2025
for JEE & Revision Notes - Differentiability in Hindi for Mock Tests for JEE Main and Advanced 2025 course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Differentiability Class 11 Notes Maths
Description
Full syllabus notes, lecture & questions for Differentiability Class 11 Notes Maths - JEE | Plus excerises question with solution to help you revise complete syllabus for Mock Tests for JEE Main and Advanced 2025 | Best notes, free PDF download
Information about Revision Notes - Differentiability
In this doc you can find the meaning of Revision Notes - Differentiability defined & explained in the simplest way possible. Besides explaining types of
Revision Notes - Differentiability theory, EduRev gives you an ample number of questions to practice Revision Notes - Differentiability tests, examples and also practice JEE
tests
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
mock tests for examination
,Summary
,Viva Questions
,MCQs
,study material
,video lectures
,Sample Paper
,past year papers
,Semester Notes
,practice quizzes
,Important questions
,Extra Questions
,Free
,Differentiability Class 11 Notes Maths
,Differentiability Class 11 Notes Maths
,shortcuts and tricks
,Differentiability Class 11 Notes Maths
,Previous Year Questions with Solutions
,Objective type Questions
,ppt
,Exam
;
Additional Information about Revision Notes - Differentiability for JEE Preparation
Revision Notes - Differentiability Free PDF Download
The Revision Notes - Differentiability is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes - Differentiability now and kickstart your journey towards success in the JEE exam.
Importance of Revision Notes - Differentiability
The importance of Revision Notes - Differentiability cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes - Differentiability
Revision Notes - Differentiability Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes - Differentiability.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes - Differentiability Notes on EduRev are your ultimate resource for success.
Revision Notes - Differentiability JEE Questions
The "Revision Notes - Differentiability JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes - Differentiability on the App
Students of JEE can study Revision Notes - Differentiability alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes - Differentiability,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes - Differentiability is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup