Maxima & Minima Revision Notes | Mock Tests for JEE Main and Advanced 2026 PDF Download
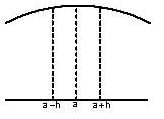
A function f(x) is said to have a local maximum at x = a if the value of f(a) is greater than all the values of f(x) in a small neighbourhood of x = a. Mathematically, f (a) > f (a – h) and f (a) > f (a + h) where h > 0, then a is called the point of local maximum.
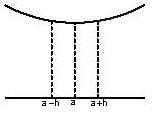
A function f(x) is said to have a local minimum at x = a, if the value of the function at x = a is less than the value of the function at the neighboring points of x = a. Mathematically, f (a) < f (a – h) and f (a) < f (a + h) where h > 0, then a is called the point of local minimum.
- A point of local maximum or a local minimum is also called a point of local extremumA point where the graph of function is continuous and has a tangent line and where the concavity changes is called point of inflexion.
- At the point of inflexion, either y” = 0 and changes sign or y” fails to exist.
- At the point of inflexion, the curve crosses its tangent at that point.
- A function cannot have point of inflexion and extrema at the same point.
- Working rules to find points of local maxima and local minima:
1. First Derivative Test: If f'(a) = 0 and f'(x) changes its sign while passing through the point x = a, then
- f(x) would have a local maximum at x = a if f'(a – 0) > 0 and f'(a + 0) < 0. It means that f'(x) should change its sign from positive to negative.
- f(x) would have local minimum at x = a if f'(a – 0) < 0 and f'(a + 0) > 0 . It means that f'(x) should change its sign from negative to positive.
- If f(x) doesn’t change its sign while passing through x = a, then f (x) would have neither a maximum nor minimum at x = a. e.g. f (x) = x3 doesn’t have any local maxima or minima at x = 0.
2. Second Derivative Test:
- Let f(x) be a differentiable function on a given interval and let f'' be continuous at stationary point. Find f'(x) and solve the equation f'(x) = 0 given let x = a, b, … be solutions.
- There can be two cases:
Case (i): If f''(a) <0 then f(a) is maximum.
Case (ii): If f ''(a) > 0 then f(a) is minimum.
In case, f''(a) = 0 the second derivatives test fails and then one has to go back and apply the first derivative test.
If f''(a) = 0 and a is neither a point of local maximum nor local minimum then a is a point of inflection.
3. nth Derivative Test for Maxima and Minima: Also termed as the generalization of the second derivative test, it states that if the n derivatives i.e. f '(a) = f''(a) = f'''(a) =………. = f n(a) = 0 and fn+1(a) ≠ 0 (all derivatives of the function up to order ‘n’ vanish and (n + 1)th order derivative does not vanish at x = a), then f (x) would have a local maximum or minimum at x = a iff n is odd natural number and that x = a would be a point of local maxima if fn+1 (a) < 0 and would be a point of local minima if fn+1 (a) > 0.
- In some questions involving determination of maxima and minima, it might become difficult to decide whether f(x) actually changes its sign while passing through x = a and here, nth derivative test can be applied.
- Global Minima & Maxima of f(x) in [a, b] is the least or the greatest value of the function f(x) in interval [a, b].
1. The function f(x) has a global maximum at the point ‘a’ in the interval I if f (a) ≥ f(x), for all x ∈ I.
2. Function f(x) has a global minimum at the point ‘a’ if f (a) ≤ f (x), for all x ∈ I.
- Global Maxima Minima always occur either at the critical points of f(x) within [a, b] or at the end points of the interval.
- Computation of Global Maxima and minima in maxima minima problems:
1. Compute the critical points of f(x) in (a, b). Let the various critical points be C1, C2, …. , Cn.
2. Next, compute the value of the function at these critical points along with the end points of the domain. Let us denote these values by f(C1), f(C2)………..f(Cn).
3. Now, compute M* = max{f(a), f(C1), f(C2)………..f(Cn), f(b)} and M** = min{f(a), f(C1), f(C2)………..f(Cn), f(b)}.Now M* is the maximum value of f(x) in [a, b] and M** is the minimum value of f(x) in [a, b]. - In order to find global maxima or minima in open interval (a, b) proceed as told above and after the first two steps, compute
M1 = max{f(C1), f(C2)………..f(Cn)} and
M2 = min{f(C1),f(C2)………..f(Cn)}. - Now if x approaches a- or if x approaches b- , the limit of f(x) > M1 or its limit f(x) < M1 would not have global maximum (or global minimum) in (a, b) but if as x approaches a- and x approaches b- , lim f(x) < M1 and lim f(x) > M2, then M1 and M2 will respectively be the global maximum and global minimum of f(x) in (a,b).
- If f(x) is a continuous function on a closed bounded interval [a,b], then f(x) will have a global maximum and a global minimum on [a,b]. On the other hand, if the interval is not bounded or closed, then there is no guarantee that a continuous function f(x) will have global extrema.
- If f(x) is differentiable on the interval I, then every global extremum is a local extremum or an end point extremum.
|
357 docs|100 tests
|
FAQs on Maxima & Minima Revision Notes - Mock Tests for JEE Main and Advanced 2026
| 1. What is the concept of maxima and minima in mathematics? |  |
| 2. How can we find the maxima and minima of a function? |  |
| 3. What is the significance of maxima and minima in real-life applications? |  |
| 4. Can a function have multiple maxima or minima? |  |
| 5. Are there any other methods to find maxima and minima apart from calculus? |  |
















