Class 6 Exam > Class 6 Notes > Mathematics Class 6 ICSE > Revision Notes: Properties of Angles and Lines - Including Parallel
Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE PDF Download
Conditions for Parallel Lines
Lines l and m are parallel if any of the following is true:
- Pairs of alternate angles are equal.
∠3 = ∠5, ∠1 = ∠7 - Pairs of corresponding angles are equal.
∠2 = ∠6, ∠4 = ∠8 - The sum of the interior (or exterior) angles on the same side of the transversal is 180°.
∠3 + ∠6 = 180° or
∠1 + ∠8 = 180°
Constructions of Specific Angles
(i) Draw a ray OA
(ii) Using a compass, with O as centre and any radius draw an arc PQ which cuts OA at P
(iii) With P as centre and same radius draw an arc to cut the arc PQ at R
(iv) Join OR and produce it to form the ray OB
(v) The ∠AOB thus formed measures 60°.
Note: To get angle of 30°, follow the above steps and then draw a angle bisector.
(i) Draw a ray OA
(ii) With O as centre and any radius draw an arc which cuts OA at P
(iii) With P as centre and same radius draw an arc to cut the arc in step (ii) at W
(iv) With Q as centre and same radius as in step (ii) draw an arc to cut the arc in step (ii) at R
(v) With Q as centre and same radius draw an arc
(vi) With R as centre and same radius draw an arc, to cut the arc in Step (v) at C
(vii) Join OC and produce it to B
(viii) The ∠AOB thus formed measures 90°
Note: To get angle of 45º, follow the above steps and then draw a angle bisector
To get angle 120°, follow steps (i) to (iv) above, and join OR and produce it to B.
Drawing a Perpendicular Bisector
(i) Draw a line segment AB of given length by using a scale
(ii) With A as centre and radius more than half of AB, draw arcs on each side of AB
(iii) With B as centre and same radius, repeat step (ii)
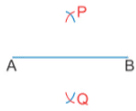(iv) Join line segment PQ, which is a perpendicular bisector to AB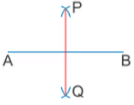
Drawing an Angle Bisector
(i) With A as centre and any radius, draw an arc cutting AB at P and AC at Q
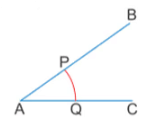
(ii) With P as centre and radius more than half of PQ, draw an arc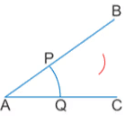
(iii) With Q as centre and same repeat step (ii)
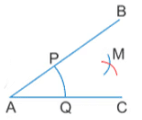(iv) Join AM and produce it to AR. The ray AR is bisector of ∠BAC
The document Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE is a part of the Class 6 Course Mathematics Class 6 ICSE.
All you need of Class 6 at this link: Class 6
|
44 videos|202 docs|24 tests
|
About this Document
Sep 23, 2025
Last updated
Document Description: Revision Notes: Properties of Angles and Lines - Including Parallel for Class 6 2025 is part of Mathematics Class 6 ICSE preparation.
The notes and questions for Revision Notes: Properties of Angles and Lines - Including Parallel have been prepared according to the Class 6 exam syllabus. Information about Revision Notes: Properties of Angles and Lines - Including Parallel covers topics
like and Revision Notes: Properties of Angles and Lines - Including Parallel Example, for Class 6 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Properties of Angles and Lines - Including Parallel.
Introduction of Revision Notes: Properties of Angles and Lines - Including Parallel in English is available as part of our Mathematics Class 6 ICSE
for Class 6 & Revision Notes: Properties of Angles and Lines - Including Parallel in Hindi for Mathematics Class 6 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 6
Exam by signing up for free. Class 6: Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE
Description
Full syllabus notes, lecture & questions for Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE - Class 6 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 6 ICSE | Best notes, free PDF download
Information about Revision Notes: Properties of Angles and Lines - Including Parallel
In this doc you can find the meaning of Revision Notes: Properties of Angles and Lines - Including Parallel defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Properties of Angles and Lines - Including Parallel theory, EduRev gives you an ample number of questions to practice Revision Notes: Properties of Angles and Lines - Including Parallel tests, examples and also practice Class 6
tests
Related Searches
Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE
,Summary
,Previous Year Questions with Solutions
,Semester Notes
,MCQs
,Exam
,mock tests for examination
,Viva Questions
,shortcuts and tricks
,video lectures
,Free
,Extra Questions
,ppt
,Important questions
,Objective type Questions
,past year papers
,practice quizzes
,Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE
,Revision Notes: Properties of Angles and Lines - Including Parallel | Mathematics Class 6 ICSE
,study material
,Sample Paper
;
Additional Information about Revision Notes: Properties of Angles and Lines - Including Parallel for Class 6 Preparation
Revision Notes: Properties of Angles and Lines - Including Parallel Free PDF Download
The Revision Notes: Properties of Angles and Lines - Including Parallel is an invaluable resource that delves deep into the core of the Class 6 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Properties of Angles and Lines - Including Parallel now and kickstart your journey towards success in the Class 6 exam.
Importance of Revision Notes: Properties of Angles and Lines - Including Parallel
The importance of Revision Notes: Properties of Angles and Lines - Including Parallel cannot be overstated, especially for Class 6 aspirants.
This document holds the key to success in the Class 6 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Properties of Angles and Lines - Including Parallel
Revision Notes: Properties of Angles and Lines - Including Parallel Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Properties of Angles and Lines - Including Parallel.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Properties of Angles and Lines - Including Parallel Notes on EduRev are your ultimate resource for success.
Revision Notes: Properties of Angles and Lines - Including Parallel Class 6 Questions
The "Revision Notes: Properties of Angles and Lines - Including Parallel Class 6 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 6 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Properties of Angles and Lines - Including Parallel on the App
Students of Class 6 can study Revision Notes: Properties of Angles and Lines - Including Parallel alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Properties of Angles and Lines - Including Parallel,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Properties of Angles and Lines - Including Parallel is prepared as per the latest Class 6 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup