Revision Notes: Ratio, Proportion and Unitary Method | Mathematics Class 6 ICSE PDF Download
Ratio
A ratio is the relationship between two quantities which expresses how many times one quantity is the other quantity of the same kind and in the same unit.
Ex. 3:4 = 3/4
- The ratio between two quantities is obtained by dividing the first quantity by the second.
𝑬𝒙:𝑨 = 𝟑𝟔 𝒂𝒏𝒅 𝑩 = 𝟐𝟒
∴ 𝑹𝒂𝒕𝒊𝒐 𝒐𝒇 𝑨 𝒂𝒏𝒅 𝑩 = 𝑨:𝑩 = 36/24 = 3/2 = 3 : 2 - The two quantities in a ratio are called its terms. The first term is called the antecedent, and the second term is called the consequent.
- A ratio is a pure number and has no unit.
- A ratio should always be expressed in its lowest terms.
- Continued ratios will be of the form 𝒂:𝒃 𝒂𝒏𝒅 𝒃:𝒄
To Convert a Fractional Ratio into a Whole Number:
- Find the LCM of the denominators
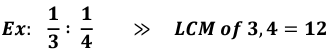
- Multiply each term of the ratio by this LCM and simplify
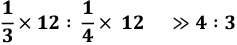
Proportion
Proportion: When four quantities are such that the ratio of the first to the second is the same as the ratio of the third to the fourth, the quantities are said to be in proportion.
𝑹𝒂𝒕𝒊𝒐𝒔 𝟏𝟒∶𝟑𝟎= 14/30 = 7/15 𝒂𝒏𝒅 𝟔𝟑∶𝟏𝟑𝟓 = 36/135 = 7/15 𝒂𝒓𝒆 𝒔𝒂𝒎𝒆, 𝟏𝟒,𝟑𝟎,𝟔𝟑,𝟏𝟑𝟓 𝒂𝒓𝒆 𝒊𝒏 𝒑𝒓𝒐𝒑𝒐𝒓𝒕𝒊𝒐𝒏 = 𝟏𝟒∶𝟑∷𝟔𝟑∶𝟏𝟑𝟓
- The first and fourth terms are called extremes
- The second and third terms are called means
- Product of extremes = Product of means
- The double colon (::) is used in place of the sign of equality (=)
- The fourth quantity is called the fourth proportion.
Properties of Proportion
- Three quantities are said to be in continued proportion if the ratio of the first to the second is the same as the ratio of the second to the third, i.e., a : b = b : c
- The second term is called the mean proportion. i. e. a : b = b : c ;
c, b is the mean proportional between a and c. - The third quantity is called the third proportion to the first and second terms.
i.e. a : b = b : c ; c is the third proportional between a and b. - Proportion a : b : c indicates three ratios, namely a : b; b : c and a : c
Unitary Method
The Unitary Method is one in which the value of a unit quantity is first obtained to find the value of any given quantity.
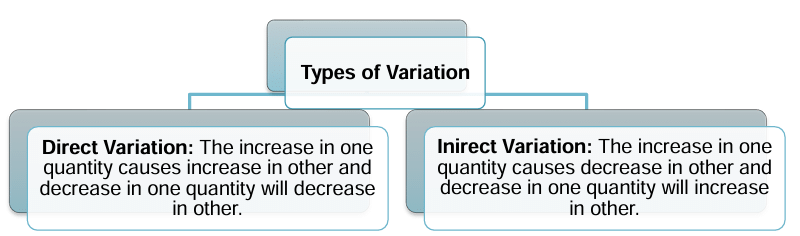
Variation Means Change
- A quantity which takes different values is called a variable.
Ex: x, y... - A quantity which does not change is called a constant.
Ex: 2, 3/4,π - Direct Proportion/Direct Variation: Let x and y be two variables such that the ratio of y to x is a constant, y varies directly with x, or y is directly proportional to x. This is represented as y/x = k : y = kx where k= the constant of proportionality.
The symbol used is"α". - Inverse Proportion/Indirect Variation: Let x and y be two variables such that the product of the two variables is a constant. i.e. xy=k : x=k/y where k= constant of proportionality.
Symbol used is"1/α".
While applying the unitary method, arrange the statement in such a way that whatever is asked to find in the question is written at the end of the statement.
Time and Work
- 𝐎𝐧𝐞 𝐝𝐚𝐲′𝐬 𝐰𝐨𝐫𝐤 = 1/𝐍𝐨 𝐨𝐟 𝐝𝐚𝐲𝐬 𝐫𝐞𝐪𝐮𝐢𝐫𝐞𝐝 𝐭𝐨 𝐜𝐨𝐦𝐩𝐥𝐞𝐭𝐞 𝐭𝐡𝐞 𝐰𝐨𝐫𝐤
- 𝐍𝐨.𝐨𝐟 𝐝𝐚𝐲𝐬 𝐫𝐞𝐪𝐮𝐢𝐫𝐞𝐝 𝐭𝐨 𝐝𝐨 𝐜𝐞𝐫𝐭𝐚𝐢𝐧 𝐰𝐨𝐫𝐤 = 1/𝐎𝐧𝐞 𝐝𝐚𝐲′𝐬 𝐰𝐨𝐫𝐤
- 𝐍𝐨.𝐨𝐟 𝐝𝐚𝐲𝐬 𝐫𝐞𝐪𝐮𝐢𝐫𝐞𝐝 𝐭𝐨 𝐜𝐨𝐦𝐩𝐥𝐞𝐭𝐞 𝐜𝐞𝐫𝐭𝐚𝐢𝐧 𝐰𝐨𝐫𝐤 = 𝐖𝐨𝐫𝐤 𝐭𝐨 𝐛𝐞 𝐜𝐨𝐦𝐩𝐥𝐞𝐭𝐞𝐝/𝐎𝐧𝐞 𝐝𝐚𝐲′𝐬 𝐰𝐨𝐫𝐤
- 𝐀 𝐢𝐬 𝐜𝐨𝐦𝐩𝐥𝐞𝐭𝐞𝐬 𝐰𝐨𝐫𝐤 𝐢𝐧 𝐱 𝐝𝐚𝐲𝐬 𝐚𝐧𝐝 𝐁 𝐢𝐧 𝐲 𝐝𝐚𝐲𝐬,𝐭𝐡𝐞𝐧 𝐎𝐧𝐞 𝐝𝐚𝐲′𝐬 𝐰𝐨𝐫𝐤 =
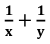
|
45 videos|298 docs|24 tests
|
FAQs on Revision Notes: Ratio, Proportion and Unitary Method - Mathematics Class 6 ICSE
| 1. What is a ratio and how is it used in mathematics? |  |
| 2. How do you simplify a ratio? |  |
| 3. Can ratios be expressed in different forms, and if so, how? |  |
| 4. What is a proportion, and how is it related to ratios? |  |
| 5. How can I apply ratios in real-life situations? |  |
















