Class 9 Exam > Class 9 Notes > Mathematics Class 9 ICSE > Revision Notes: Trigonometry
Revision Notes: Trigonometry | Mathematics Class 9 ICSE PDF Download
- Trigonometry is the study of relationship between the sides and the angles of the triangle.
- The word trigonometry is derived from the Greek words ‘tri’ meaning three, ‘gon’ meaning sides and ‘metron’ meaning measure.
- Angle measured in anticlockwise direction is taken as positive angle.
- Angle measured in clockwise direction is taken as negative angle.
- Ratio of the sides of the right triangle with respect to the acute angles is called trigonometric ratios of the angle.
- Trigonometric ratios of acute angle A in right triangle ABC:
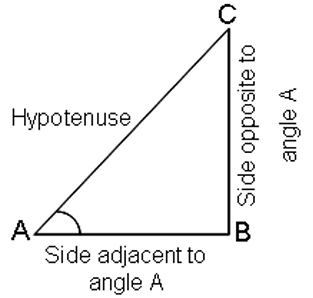
- Each trigonometric ratio is a real number. It has no unit.
- Only symbols cosine, sine, tangent, cotangent, sec and cosec have no meaning.
- (sinθ)n is generally written as sinn θ, n being a positive integer. Similarly, other trigonometric ratios can also be written.
- The values of the trigonometric ratios of an angle do not vary with the length of the sides of the triangle, if the angles remain the same.
- Pythagoras theorem: In a right triangle, square of the hypotenuse is equal to the sum of the square of the other two sides.
- When any two sides of a right triangle are given, its third side can be obtained by using Pythagoras theorem.
- Relation between trigonometric ratios:
(i) tanθ = sinθ/cosθ
(ii) cosecθ = 1/sinθ
(iii) secθ = 1/cosθ
(iv) cotθ =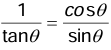
- Values of Trigonometric ratios of some specific angles:
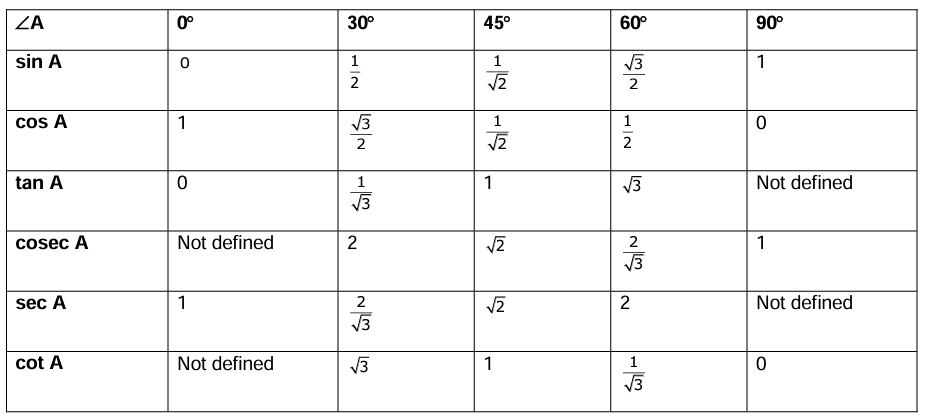
- The value of sin A or cos A never exceeds 1, whereas the value of sec A or cosec A is always greater than 1 or equal to 1.
- The value of sinθ increases from 0 to 1 when θ increases from 0° to 90°.
- The value of cosθ decreases from 1 to 0 when θ increases from 0° to 90°.
- Trigonometric ratios of complementary angles:
(i) sin (90° – A) = cos A
(ii) cos (90° – A) = sin A
(iii) tan (90° – A) = cot A
(iv) cot (90° – A) = tan A
(v) sec (90° – A) = cosec A
(vi) cosec (90° – A) = sec A - An equation involving trigonometric ratios of an angle, say θ, is termed as a trigonometric identity if it is satisfied by all values of θ.
- Basic trigonometric identities:
(i) sin2θ + cos2θ = 1
(ii) 1 + tan2θ = sec2θ
(iii) 1 + cot2θ = sec2θ
The document Revision Notes: Trigonometry | Mathematics Class 9 ICSE is a part of the Class 9 Course Mathematics Class 9 ICSE.
All you need of Class 9 at this link: Class 9
|
64 videos|138 docs|28 tests
|
FAQs on Revision Notes: Trigonometry - Mathematics Class 9 ICSE
| 1. What is the basic definition of trigonometry? |  |
Ans. Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of triangles, particularly right-angled triangles. It involves the use of various functions like sine, cosine, and tangent to relate these angles and sides.
| 2. What are the main trigonometric ratios? | |
Ans. The main trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). In a right-angled triangle, these ratios are defined as follows:
- Sine is the ratio of the length of the opposite side to the length of the hypotenuse (sin = opposite/hypotenuse).
- Cosine is the ratio of the length of the adjacent side to the length of the hypotenuse (cos = adjacent/hypotenuse).
- Tangent is the ratio of the length of the opposite side to the length of the adjacent side (tan = opposite/adjacent).
| 3. How can I remember the trigonometric ratios? | |
Ans. A common mnemonic to remember the trigonometric ratios is "SOH-CAH-TOA." This stands for:
- SOH: Sine = Opposite / Hypotenuse
- CAH: Cosine = Adjacent / Hypotenuse
- TOA: Tangent = Opposite / Adjacent.
Using this mnemonic can help students recall the definitions of the sine, cosine, and tangent functions easily.
| 4. What is the Pythagorean theorem and how is it related to trigonometry? | |
Ans. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b). This can be expressed as a² + b² = c². In trigonometry, this theorem is used to derive the relationships between the trigonometric ratios and to solve various problems involving right triangles.
| 5. How do I solve basic trigonometric equations? | |
Ans. To solve basic trigonometric equations, you can follow these steps:
1. Isolate the trigonometric function on one side of the equation.
2. Use known values of trigonometric ratios or identities to simplify the equation.
3. Find the general solutions using the unit circle or reference angles if necessary.
4. Finally, check for any restrictions based on the domain of the trigonometric function.
About this Document
4.92/5
Rating
Oct 02, 2025
Last updated
Document Description: Revision Notes: Trigonometry for Class 9 2025 is part of Mathematics Class 9 ICSE preparation.
The notes and questions for Revision Notes: Trigonometry have been prepared according to the Class 9 exam syllabus. Information about Revision Notes: Trigonometry covers topics
like and Revision Notes: Trigonometry Example, for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Trigonometry.
Introduction of Revision Notes: Trigonometry in English is available as part of our Mathematics Class 9 ICSE
for Class 9 & Revision Notes: Trigonometry in Hindi for Mathematics Class 9 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 9
Exam by signing up for free. Class 9: Revision Notes: Trigonometry | Mathematics Class 9 ICSE
Description
Full syllabus notes, lecture & questions for Revision Notes: Trigonometry | Mathematics Class 9 ICSE - Class 9 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 9 ICSE | Best notes, free PDF download
Information about Revision Notes: Trigonometry
In this doc you can find the meaning of Revision Notes: Trigonometry defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Trigonometry theory, EduRev gives you an ample number of questions to practice Revision Notes: Trigonometry tests, examples and also practice Class 9
tests
Related Searches
Previous Year Questions with Solutions
,study material
,Free
,mock tests for examination
,Revision Notes: Trigonometry | Mathematics Class 9 ICSE
,past year papers
,video lectures
,Summary
,Exam
,MCQs
,Viva Questions
,Revision Notes: Trigonometry | Mathematics Class 9 ICSE
,Objective type Questions
,Extra Questions
,Revision Notes: Trigonometry | Mathematics Class 9 ICSE
,Semester Notes
,shortcuts and tricks
,Sample Paper
,ppt
,Important questions
,practice quizzes
,
Additional Information about Revision Notes: Trigonometry for Class 9 Preparation
Revision Notes: Trigonometry Free PDF Download
The Revision Notes: Trigonometry is an invaluable resource that delves deep into the core of the Class 9 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Trigonometry now and kickstart your journey towards success in the Class 9 exam.
Importance of Revision Notes: Trigonometry
The importance of Revision Notes: Trigonometry cannot be overstated, especially for Class 9 aspirants.
This document holds the key to success in the Class 9 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Trigonometry
Revision Notes: Trigonometry Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Trigonometry.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Trigonometry Notes on EduRev are your ultimate resource for success.
Revision Notes: Trigonometry Class 9 Questions
The "Revision Notes: Trigonometry Class 9 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 9 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Trigonometry on the App
Students of Class 9 can study Revision Notes: Trigonometry alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Trigonometry,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Trigonometry is prepared as per the latest Class 9 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily