Rotation about a moving axis | Additional Documents & Tests for IIT JAM PDF Download

The general motion of a rigid body tumbling through space may be described as a combination of translation of the body’s centre of mass and rotation about an axis through the centre of mass. The linear momentumof the body of mass M is given by
p = mv_c

where v_c is the velocity of the centre of mass. Any change in the momentum is governed by Newton’s second law, which states that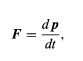 

where F is the net force acting on the body. The angular momentum of the body with respect to any reference point may be written as
L = L_c + r × p

where L_c is the angular momentum of rotation about an axis through the centre of mass, r is a vector from the reference point to the centre of mass, and r × p is therefore the angular momentum associated with motion of the centre of mass, acting as if all the body’s mass were concentrated at that point. The quantity L_c in equation is sometimes called the body’s spin, and r × p is called the orbital angular momentum. Any change in the angular momentum of the body is given by the torque equation,
L = L_c + r × p

An example of a body that undergoes both translational and rotational motion is the Earth, which rotates about an axis through its centre once per day while executing an orbit around the Sun once per year. Because the Sun exerts no torque on the Earth with respect to its own centre, the orbital angular momentum of the Earth is constant in time. However, the Sun does exert a small torque on the Earth with respect to the planet’s centre, owing to the fact that the Earth is not perfectly spherical. The result is a slow shifting of the Earth’s axis of rotation, known as the precession of the equinoxes (see below).
The kinetic energy of a body that is both translating and rotating is given by

where I is the moment of inertia and ω is the angular velocity of rotation about the axis through the centre of mass.
A common example of combined rotation and translation is rolling motion, as exhibited by a billiard ball rolling on a table, or a ball or cylinder rolling down an inclined plane. Consider the latter example, illustrated in Figure. Motion is impelled by the force of gravity, which may be resolved into two components, F_N, which is normal to the plane, and F_p, which is parallel to it. In addition to gravity, friction plays an essential role. The force of friction, written as f, acts parallel to the plane, in opposition to the direction of motion, at the point of contact between the plane and the rolling body. If f is very small, the body will slide without rolling. If f is very large, it will prevent motion from occurring. The magnitude of f depends on the smoothness and composition of the body and the plane, and it is proportional to F_N, the normal component of the force.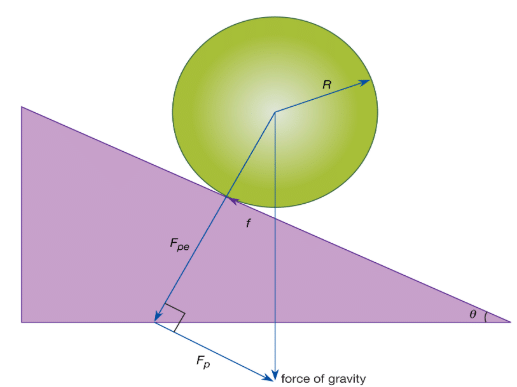

Figure: Rolling motion.

Consider a case in which f is just large enough to cause the body (sphere or cylinder) to roll without slipping. The motion may be analyzed from the point of view of an axis passing through the point of contact between the rolling body and the plane. Remarkably, the point of contact may always be regarded to be instantaneously at rest. To understand why, suppose that the rolling body has radius R and angular velocity ω about its centre-of-mass axis. Then, with respect to its own axis, each point on the circular cross section in Figure moves with instantaneous tangential linear speed v_c = Rω. In particular, the point of contact is moving backward with this speed relative to the centre of mass. But with respect to the inclined plane, the centre of mass is moving forward with exactly this same speed. The net effect of the two equal and opposite speeds is that the point of contact is always instantaneously at rest. Therefore, although friction acts at that point, no work is done by friction, so mechanical energy (potential plus kinetic) may be regarded as conserved.
With respect to the axis through the point of contact, the torque is equal to RF_p, giving rise to an angular acceleration α given by I_pα = RF_p, where I_p is the moment of inertia about the point-of-contact axis and can be determined by applying equation relating moments of inertia about parallel axes (I_p = I + MR²). Thus,
I = Ic + Mr²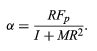

From this result, the motion of the body is easily obtained using the fact that the velocity of the centre of mass is v_c = Rω and hence the linear acceleration of the centre of mass is a_c = Rα.
Notice that, although without friction no angular acceleration would occur, the force of friction does not affect the magnitude of α. Because friction does no work, this same result may be obtained by applying energy conservation. The situation also may be analyzed entirely from the point of view of the centre of mass. In that case, the torque is −fR, but f also provides a linear force on the body. The f may then be eliminated by using Newton’s second law and the fact that the torque equals the moment of inertia times the angular acceleration, once again leading to the same result.
One more interesting fact is hidden in the form of equation. The parallel component of the force of gravity is given by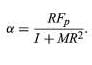

Fp = Mg sinθ
where θ is the angle of inclination of the plane. The moment of inertia about the centre of mass of any body of mass M may be written
I = Mk²

where k is a distance called the radius of gyration. Comparison to equation shows that k is a measure of how far from the centre of mass the mass of the body is concentrated. Using equations, one finds that
Fp = Mg sinθ
I = Mk²

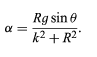
Thus, the angular acceleration of a body rolling down a plane does not depend on its total mass, although it does depend on its shape and distribution of mass. The same may be said of a_c, the linear acceleration of the centre of mass. The acceleration of a rolling ball, like the acceleration of a freely falling object, is independent of its mass. This observation helps to explain why Galileo was able to discover many of the basic laws of dynamicsin gravity by studying the behaviour of balls rolling down inclined planes.