Rotation of Objects | Know Your Aptitude Class 6 To 8 - Class 8 PDF Download

Rotation Definition

Rotation means the circular movement of an object around a centre. It is possible to rotate different shapes by an angle around the centre point. Mathematically, a rotation means a map. All the rotations around a fixed point that make a group under a structure are called the rotation group of a unique space. When coming to the three-dimensional shapes, we can turn or rotate the objects about an infinite number of imaginary lines known as rotational axes. Now one might have the question of what the rotation of axes is? Here is the answer. The rotations around X, Y and Z axes are known as the principal rotations. The rotations around any axis can be performed by taking the rotation around the X-axis, followed by the Y-axis and then finally the z-axis.

Rotation Formula

Rotation can be done in both directions like clockwise as well as counterclockwise. The most common rotation angles are 90°, 180° and 270°. However, a clockwise rotation implies a negative magnitude, so a counterclockwise turn has a positive magnitude. There are specific rules for rotation in the coordinate plane.
They are:

Rotation Matrix

A rotation matrix is a matrix used to perform a rotation in a Euclidean space. In a two-dimensional cartesian coordinate plane system, the matrix R rotates the points in the XY-plane counterclockwise through an angle θ about the origin.
The matrix R can be represented as: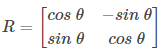

If we want to perform the rotation operation using the rotation matrix R, the position of each point in the plane is represented by a column vector “v”, which contains the coordinate point. With the help of matrix multiplication Rv, the rotated vector can be obtained.

Rotational Symmetry

In geometry, many shapes have rotational symmetry like circles, squares, and rectangles, etc. All the regular polygons have rotational symmetry. If an object is rotated around its centre, the thing appears precisely like before the rotation. Then the object is said to have rotational symmetry. We can identify the rotation symmetry in many ways. One of the easiest ways to find the order of symmetry is to count the number of times the figure coincides with itself when it rotates through 360°. 

Rotation Images

The below figure shows the rotational symmetry of a geometric figure: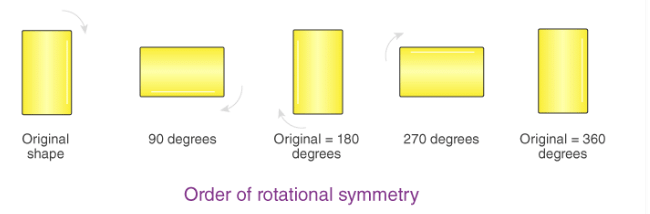

The above example shows the rotation of a rectangle 90° each time. The rectangle has the rotational symmetry of order 2 because when it is rotated twice, we get the original shape at 180° and again, when it is rotated twice, the original form is obtained at 360°. So, the order of rotational symmetry of the rectangle is 2.

Rotation Example

In this section, you can observe the real life examples of rotation that may denote the axis rotation.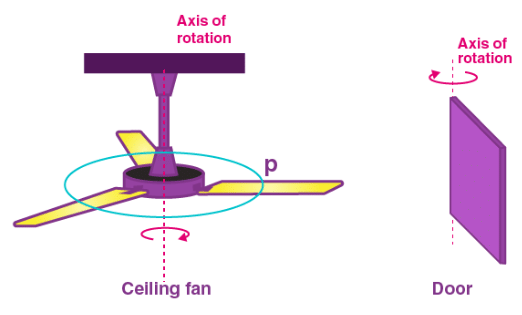

In the above figure, the motion of a ceiling fan and the movement of a door shows the axis of rotation.