Sample Question Paper- 2 | Mathematics (Maths) Class 8 PDF Download
Class - VIII
Mathematics
Time - 3 hrs
M.M. - 80 Marks
General Instructions :
1. All questions are compulsory.
2. The question paper consist of 30 questions divided into four sections A, B, C and D. Section A comprises of 6 questions of 1 mark each, Section B comprises of 6 questions of 2 marks each, Section C comprises of 10 questions of 3 marks each and Section D comprises of 8 questions of 4 marks each.
3. There is no overall choice. 4. Use of calculator is not allowed.
SECTION ‘A’ (1 mark each)
Q.1. Check the divisibility of the following numbers by 9 :
(a) 108
(b) 616
Ans. (a) 108
∵ 1 + 0 + 8 = 9
and 9 is divisible by 9
∴ 108 is divisible by 9.
(b) 616
We have, 6 + 1 + 6 = 13
and 13 is not divisible by 9
∴ 616 is also not divisible by 9.
Q.2. Find the number of digits in the square root of 4489. (Without any calculation).
Ans. For 4489, n = 4 [Even number]
∴ Number of digits in its square root = 
Q.3. Factorise y2 – 2y – 15
Ans.
y2 – 2y – 15
y2 – (5 – 3)y – 15
y2 – 5y + 3y – 15
y(y – 5) + 3 (y – 5)
(y – 5) (y + 3)
Q.4. What is Euler formula.
Ans. Euler ’s formula for any polyhedron is,
F + V – E = 2
where F stands for number of faces, V for number of vertices and E for number of edges.
Q.5. Factorise : 9x2 – 1
Ans. 9x2 – 1 = (3x)2 – (1)2
= (3x + 1) (3x – 1)
Q.6. Find the product of (– 3x2y) × (4x2y – 3xy2 + 4x – 5y).
Ans. (– 3x2y) × (4x2y – 3xy2 + 4x – 5y) = – 12x4y2 + 9x3y3 – 12x3y + 15x2y2
SECTION ‘B’ (2 marks each)
Q.7. If each edge of a cube is doubled
(a) How many times will its surface area increase ?
(b) How many times will its volume increase ?
Ans. (a) Let the edge of cube be x
According to question, edge of cube is doubled = 2x
The surface area of cube when edge is doubled = 6l2
= 6 × (2x)2
= 6 × 4x2
= 4 × (6x2)
The surface area of cube is 4 time increase.
(b) The volume of cube when edge is doubled
= (2x)3
= 8x3
The volume of cube is 8 time increase, when edge is doubled.
Q.8. (a) Express 49 as the sum of 7 odd numbers.
(b) Express 121 as the sum of 11 odd number.
Ans. (a) 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13
(b) 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
Q.9. Using prime factorisation, find the cube root of 5832.
Ans. The prime factorisation of 5832 is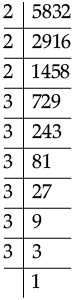
5832 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Therefore, 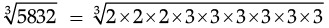
= 2 × 3 × 3
= 18
Q.10. Find the side of a square whose area is equal to the area of a rectangle with sides 6.4 m and 2.5 m.
Ans. Given, Area of square = Area of rectangle
a2 = l × b
a2 = 6.4 × 2.5
a2 = 16
a = 4
So, the side of square is 4 m.
Q.11. On sunday 845 people went to zoo. On Monday only 169 people went. What is the percent decrease in the people visiting the zoo on Monday.
Ans. People went to the Zoo on Sunday = 845
People went to the Zoo on Monday = 169
Decrease in the people = 845 – 169 = 676
Decrease value of Monday = Decrease % of 845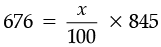
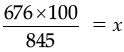
x = 80
∴ 80% people decreased on Monday.
Q.12. Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonal is 8 cm long, find the length of the other diagonal.
Ans. We have, Area of rhombus = base × altitude
= 5 × 4.8
= 24 cm2
Also, Area of rhombus = 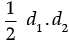
24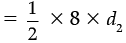
⇒ d2 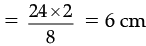
∴ Area of rhombus = 24 m2
Other diagonal of rhombus = 6 cm.
SECTION ‘C’
Q.13. Verify x + y = y + x, if x =  and y =
and y =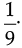
Ans. 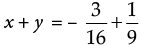
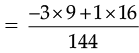 [∵ LCM of 16 and 9 is 144]
[∵ LCM of 16 and 9 is 144]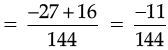
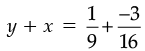
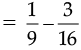
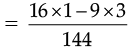
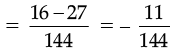
⇒ x + y = y + x.
Q.14. If 756 x is divisible by 11, where x is a digit find the value of x.
Ans. Sum of digits of odd place = 7 + 6 = 13
Sum of digit of even place = 5 + x
Difference (x + 5) – 13 = x – 8 (i)
Now (x – 8) should be equal 0 or a multiple of 11 (i.e., 11, 22, 33, ... etc)
x – 8 = 0
⇒ x = 8 or x – 8 = 11
x = 11 + 8 = 19
Since, x is a digit, so it can take value from 0 – 9
Hence, x = 8
Required number is 7568.
Q.15. Amina thinks of a number and subtracts 5/2 from it. She multiplies the result by 8. The result now obtained is 3 times the same number she thought of. What is the number ?
Ans. Let the number be x.
(d) Construct ∠ABY = 85° at B. According to question,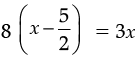
or, 8x – 20 = 3x
or, 8x – 3x = 20 [Transposing 3x to LHS and 20 to RHS]
or, 5x = 20 [Dividing both sides by 5]
or, 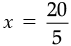
or, x = 4
Hence, the required number is 4.
Q.16. Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will be need to form a cube?
Ans. The sides of a cuboid are 5 cm, 2 cm, 5 cm.
Let Parikshit needs n such type of cuboid to make it cube.
Hence, the volume of cuboids = n × 5 × 2 × 5
Since, this volume forms a cube and the volume of a cube is a perfect cube, of positive integer. To form 5 × 5 × 2 a perfect cube, we need the factor 5 × 2 × 2 = 20. Hence, n = 20.
Therefore, Parikshit needs 20 such type of cuboids to make it cube.
Q.17. Construct a quadrilateral ABCD , given AB = 5·1 cm, AD = 4 cm, BC = 2.5 cm, ∠A = 60° and ∠B = 85°.
Ans. Steps of Construction :
(a) Draw AB = 5·1 cm.
(b) Construct ∠XAB = 60° at A.
(c) With A as centre and radius AD = 4 cm, cut off AD = 4 cm along AX.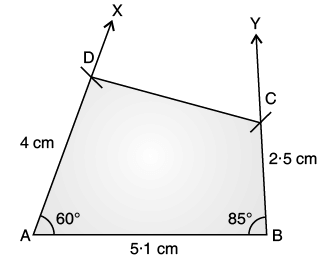
(d) Construct ∠ABY = 85° at B.
(e) With B as centre and radius BC = 2·5 cm cut off BC = 2·5 cm along BY.
(f) Join CD.
Thus, ABCD is the required quadrilateral.
Q.18. Construct a quadrilateral ABCD in which AB = 5·6 cm, BC = 4·1 cm, CD = 4·4 cm, AD = 3·3 cm and ∠A = 75°.
Ans. Steps of Construction :
(a) Draw a line segment AB = 5·6 cm.
(b) Making ∠A = 75° with centre A.
(c) Draw two arcs of radius 4·1 cm and 4·4 cm with centre B and D both arcs intersects each other at point C.
(d) Join BC and CD, then ABCD is a required quadrilateral.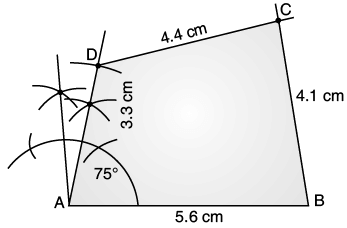
Q.19. The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
Ans. Here, l = 7 m, b = 6 m, h = 15 m
Volume of cuboid = l × b × h
= 7 × 6 × 15
= 630 m3
Since, 1 m3 = 1000 L
∴ Capacity of water in reservoir
= 630 × 1000
= 630000 L
Since, 8400 L water 5 pumped our
∴ Water left in reservoir = 630000 – 8400
= 621600 L
= 621.6 m3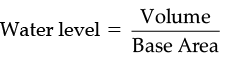
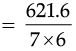
= 14.8 m
Fall in water level = 15 – 14.8
= 0.2 m or 20 cm
Q.20. By what number should 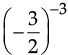 be divided so that the quotient is
be divided so that the quotient is 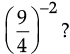
Ans. Let the required number = x
According to problem,
or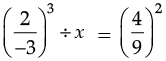
or 
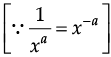
or 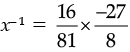
or 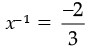
or 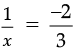
or 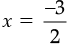
Hence, required number = 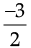
Q.21. A number is increased by 20% and then it is decreased by 20%. Find the net increase or decrease percent.
Ans. Let the number be 100
Increase in the number = 20% of 100 = 20
So, increased number = 100 + 20 = 120
Decrease in the number = 20% of 120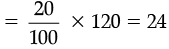
So, new number = 120 – 24 = 96
Net decrease = 100 – 96 = 4
Hence, net decrease per cent = 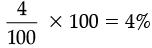
Q.22. Vishakha offers a discount of 20% on all the items at her shop and still makes a profit of 12%. What is the cost price of an article marked at Rs. 280 ?
Ans. Marked Price = Rs 280
Discount = 20% of Rs. 280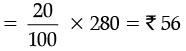
So, selling price = Rs. (280 – 56)
= Rs. 224
Let the cost price be Rs. 100
Profit = 12% of Rs. 100
= Rs. 12
So selling price = Rs. (100 + 12) = Rs. 112
If the selling price is Rs. 112, cost price = Rs. 100
If the selling price is Rs. 224, cost price =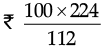
= Rs. 200.
SECTION ‘D’ (4 marks each)
Q.23. A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time (a) the length of the shadow cast by another pole 10 m 50 m high (b) the height of a pole which cast a shadow 5 m long.
Ans. (a) Let the length of the shadow be x m.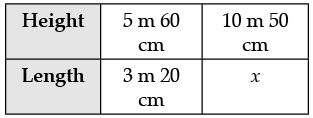
5 m 60 cm = 5.60 m
3 m 20 cm = 3.20 m
10 m 50 cm = 10.50 m
∴ 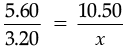
⇒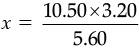
⇒ x = 6 m
(b) Let the height of a pole be y m.
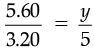
⇒ 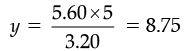
or y = 8 m 75 cm
Q.24. (a) After 12 years I shall be 3 times as old as I was 4 years ago. Find my present age.
(b) Verify that x = 4 is a root of the equation 2x – 3 = 5.
Ans. (a) Let my present age = x years
After 12 years my age = (x + 12) years
4 years ago my age = (x – 4) years
According to question,
or x + 12 = 3x – 12
or x – 3x = – 12 – 12
or – 2x = – 24
or 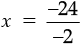
or x = 12
Therefore, my present age = 12 years.
(b) Since, 2x – 3 = 5
Putting, x = 4 then
LHS = 2x – 3
= 2 × 4 – 3 = 8 – 3 = 5
and RHS = 5
Hence, LHS = RHS = 5 [Hence,Verified]
25. Factorise :
(a) a4 – b4
(b) p4 – 81
(c) x4 – (y + 2)4
(d) x4 – (x – z)4
(e) a4 – 2a2b2 + b4
Ans. (a) Using a2 – b2 = (a – b) (a + b)
a4 – b4 = (a2 )2 – (b2)2
= (a2 + b2) (a2 – b2)
= (a2 + b2) (a + b) (a – b)
(b) p4 – 81 = (p2)2 – (9)2
= (p2 + 9) (p2 – 9) [a2 – b2 = (a + b) (a – b)]
= (p2 + 9) (p – 3) (p + 3)
(c) x4 – (y + 2)4 = (x2)2 – [(y + 2)2]2
= [(x2) + (y + 2)2] [(x2) – (y + 2)2]
= [(x)2 + (y + 2)2] [(x – y – z) (x + y + 2)]
(d) x4 – (x – z)4 = (x2)2 – [(x – z)2]2
= [x2 – (x – z)2] [x2 + (x – z)2]
= [(x – x + z) (x + x – z)] [(x2 + (x –z)2]
= z (2x – z) [x2 + (x)2 + (z)2 – 2xz]
= z (2x – z) [2x2 – 2xz + z2]
(e) a4 – 2a2b2 + b4 = (a2)2 + (b2)2 – 2 (a2) (b2)
= (a2 – b2)2
= [(a2 – b2) (a2 + b2)]
= [(a – b) (a + b) (a2 + b2)]
Q.26. (a) A cylindrical tank has a capacity of 5632 m3. If the diameter of its base is 16 m. Find its depth.
(b) If side of square is 14 cm, then find the area of semi-circle as shown in the figure.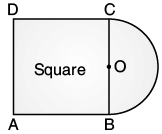 Ans. Let the depth of the cylindrical tank = h
Ans. Let the depth of the cylindrical tank = h
and Radius of its base (r) = 8 m
Then, the capacity of the tank = Volume of the tank
= πr2h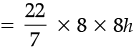
Thus, 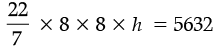
or 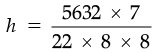
or h = 28 m
Hence, the depth of the cylindrical tank = 28 m
(b) Since side of square = 14 cm
Then, diameter of semi circle = 14 cm
Therefore, radius of semi circle (r) = 14/2
= 7 cm
Thus, Area of semi circle = 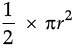
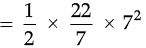
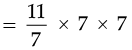
= 77 cm2
Q.27. (a) Draw the graph of the function y = 3x + 1.
(b) The given graph represents the total runs scored by two batsmen A and B, during each of the ten different matches in the year 2014.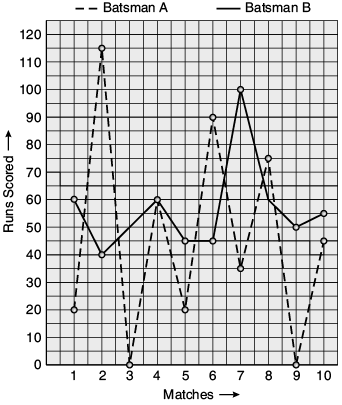 Study the graph and answer the following questions :
Study the graph and answer the following questions :
(a) What information is given on the two axes ?
(b) Which line shows the runs scored by batsman A ?
Ans. Let y = 3x + 1
Putting x = 0, 1, 2, in equation (i)
at x = 0 then
y = 3 × 0 + 1 = 1
at
x = 1 then y = 3 × 1 + 1 = 3 + 1 = 4
ata x = 2 then
y = 3 × 2 + 1 = 6 + 1 = 7
Thus
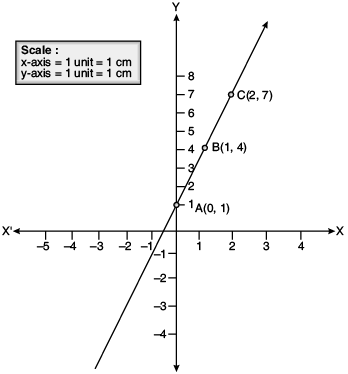
(b) (i) The horizontal axis (or the x-axis) indicates the matches played during the year 2014. The vertical axis (or the y-axis) shows the total runs scored in each match.
(ii) The dotted line shows the runs scored by Batsman A. (This is already indicated at the top of the graph).
Q.28. Construct a parallelogram ABCD in which AB =4 cm, BC = 5 cm and B = 60°.
Ans. Opposite sides of a parallelogram (|| gm) are equal.
AB = DC = 4cm
BC = AD = 5cm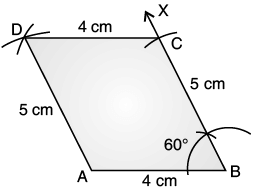
Steps of Construction
(a) Draw A B = 4 cm.
(b) Draw ray BX such that ∠ABX =60°.
(c) Mark a point C such that BC = 5 cm.
(d) With C and A as centre, draw arcs intersecting at a point D respectively ABCD is the required parallelogram.
Q.29. (a) Find the amount of Rs. 50000 after 2 years compounded annually. The rate of interest being 8% p.a. during the first year and 9% p.a. during the second year. Also, find the compound interest.
(b) If (a) decreased value = P 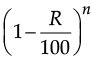 and (b) depreciated value = P
and (b) depreciated value = P  then select right answer.
then select right answer.
Ans. (a) Here P = ` 50000, R1 = 8% p.a. and R2 = 9% p.a
Since, 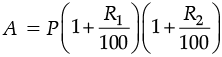

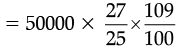
Amount = Rs. 58860
Therefore C.I. = A – P
= 58860 – 50000
= Rs. 8860
(b) (a) is right answer.
Q.30. Divide 63 (p4 + 5p3 – 24p2) by 9p (p + 8)
Ans. We have, 63 (p4 + 5p3 – 24p2) / 9p(p + 8)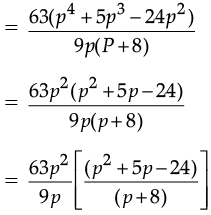
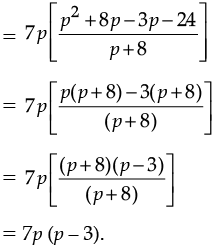
|
81 videos|423 docs|31 tests
|
FAQs on Sample Question Paper- 2 - Mathematics (Maths) Class 8
| 1. What is the importance of sample question papers in Class 8 exams? |  |
| 2. How can students effectively use sample question papers for Class 8 exams? |  |
| 3. Are the sample question papers for Class 8 exams available online? |  |
| 4. Can solving sample question papers guarantee success in Class 8 exams? |  |
| 5. How many sample question papers should a student solve for Class 8 exams? |  |





















