Scalar, vector, tensor functions
Having got an introduction to algebra of tensors we next focus on tensor calculus. Here we shall understand the meaning of a function and define what we mean by continuity and derivative of a function.
A function is a mathematical correspondence that assigns exactly one element of one set to each element of the same or another set. Thus, if we consider scalar functions of one scalar variable, then for each element (value) in the subset of the real line one associates an element in the real line or in the space of vectors or in the space of second order tensors. For example, Φ = Φ( t), u = û(t) = ui(t)ei , A = Â(t) = Aij (t)ei ⊗ ej are scalar valued, vector valued, second order tensor valued scalar functions with a set of Cartesian basis vectors assumed to be fixed. The components ui(t) and Aij(t) are assumed to be real valued smooth functions of t varying over a certain interval.
The first derivative of the scalar function Φ is simply Φ = dΦ/dt. Recollecting from a first course in calculus, dΦ/dt stands for that unique value of the limit

The first derivative of u and A with respect to t (rate of change) denoted by ù = du/dt and À = dA/dt, is given by the first derivative of their associated components.
Since, dei/dt = o, i = 1, 2, 3, we have
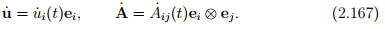
In general, the nth derivative of u and A (for any desired n) denoted by dnu/dtn and dnA/dtn , is a vector-valued and tensor-valued function whose components are dnui/dtn and dnAij/dtn , respectively. Again we have assumed that dei/dt = o.
By applying the rules of differentiation, we obtain the identities:

where Φ is a scalar valued scalar function, u and v are vector valued scalar function, A and B are second order tensor valued scalar function. Here and elsewhere in this notes, the overbars cover the quantities to which the dot operations are applied.
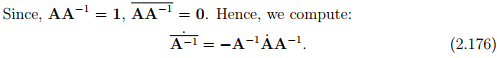
A tensor function is a function whose arguments are one or more tensor variables and whose values are scalars, vectors or tensors. The functions Φ(B), u(B), and A(B) are examples of so-called scalar-valued, vector-valued and second order tensor-valued functions of one second order tensor variable B, respectively. In an analogous manner, Φ(v), u(v), and A(v) are scalarvalued, vector-valued and second order tensor-valued functions of one vector variable v, respectively.
Let  denote the region of the vector space that is of interest. Then a scalar field Φ, defined on a domain
denote the region of the vector space that is of interest. Then a scalar field Φ, defined on a domain  , is said to be continuous if
, is said to be continuous if
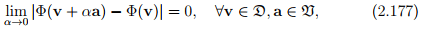
where 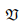 denote the set of all vectors in the vector space. The properties of continuity are attributed to a vector field u and a tensor field A defined on
denote the set of all vectors in the vector space. The properties of continuity are attributed to a vector field u and a tensor field A defined on 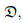 if they apply to the scalar field u · a and a · Ab ∀ a and b
if they apply to the scalar field u · a and a · Ab ∀ a and b 
Consider a scalar valued function of one second order tensor variable A, Φ(A). Assuming the function Φ is continuous in A, the derivative of Φ with respect to A, denoted by 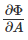 , is the second order tensor that satisfies
, is the second order tensor that satisfies
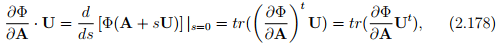
for any second order tensor U.
Example: If Φ(A) = det(A), find 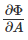 , both when A is invertible and when it is not.
, both when A is invertible and when it is not.
Taking trace of the Cayley-Hamilton equation (2.142) and rearranging we get
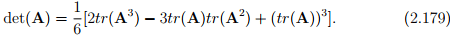
Hence,
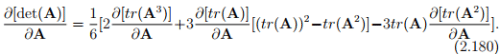
Using the properties of trace and dot product we find that
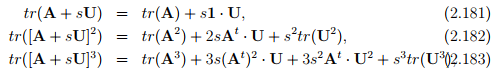
from which, we deduce that
∂ 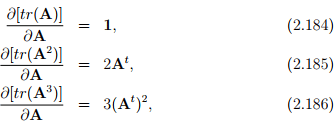
using equation (2.178). Substituting equations (2.184) through (2.186) in (2.180) we get
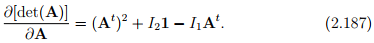
If A is invertible, then multiplying (2.142) by A−t and rearranging we get
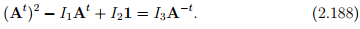
In light of the above equation, (2.187) reduces to
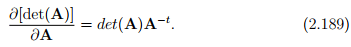
Next, we consider a smooth tensor valued function of one second order tensor variable A, f(A). As before, the derivative of f with respect to A, denoted by 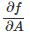 , is the fourth order tensor that satisfies
, is the fourth order tensor that satisfies
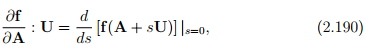
for any second order tensor U.
It is straight forward to see that when f(A) = A, where A is any second order tensor, then (2.190) reduces to

hence, 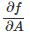 = II, the fourth order unit tensor where we have used equation (2.128a).
= II, the fourth order unit tensor where we have used equation (2.128a).
If f(A) = At where A is any second order tensor, then using (2.190) it can be shown that 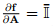 obtained using equation (2.128b).
obtained using equation (2.128b).
Now, say the tensor valued function f is defined only for symmetric tensors, and that f(S) = S, where S is a symmetric second order tensor. Compute the derivative of f with respect to S, i.e., 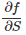 .
.
First, since the function f is defined only for symmetric tensors, we have to generalize the function for any tensor. This is required because U is any second order tensor. Hence, 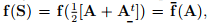 where A is any second order tensor. Now, find the derivative
where A is any second order tensor. Now, find the derivative 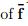 with respect to A and then rewrite the result in terms of S. The resulting expression is the derivative of f with respect to S. Hence,
with respect to A and then rewrite the result in terms of S. The resulting expression is the derivative of f with respect to S. Hence,

Substituting the above in equation (2.190) we get

Thus,

Consequently,

Example - 1: Assume that A is an invertible tensor and f(A) = A−1 .
Then show that
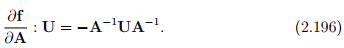
Recalling that all invertible tensors satisfy the relation AA−1 = 1, we obtain
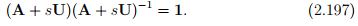
Differentiating the above equation with respect to s
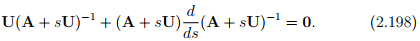
Evaluating the above equation at s = 0, and rearranging
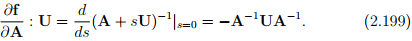
Hence proved.
Example - 2: Assume that S is an invertible symmetrical tensor and f(S) = S−1 . Find 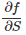 .
.
As before generalizing the given function, we have 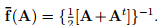
Following the same steps as in the previous example we obtain:

Differentiating the above equation with respect to s and evaluating at s = 0 and rearranging we get
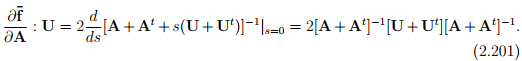
Therefore,
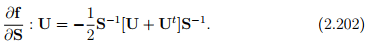
Let Φ be a smooth scalar-valued function and A, B smooth tensor-valued functions of a tensor variable C. Then, it can be shown that
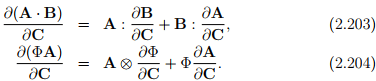
denote the region of the vector space that is of interest. Then a scalar field Φ, defined on a domain
, is said to be continuous if
denote the set of all vectors in the vector space. The properties of continuity are attributed to a vector field u and a tensor field A defined on
if they apply to the scalar field u · a and a · Ab ∀ a and b
, is the second order tensor that satisfies
, both when A is invertible and when it is not.
, is the fourth order tensor that satisfies
= II, the fourth order unit tensor where we have used equation (2.128a).
obtained using equation (2.128b).
.
where A is any second order tensor. Now, find the derivative
with respect to A and then rewrite the result in terms of S. The resulting expression is the derivative of f with respect to S. Hence,
.
























