Second Law of Thermodynamics & Entropy | Kinetic Theory & Thermodynamics - Physics PDF Download
| Table of contents |

|
| Second Law of Thermodynamics |

|
| Heat Engines |

|
| Efficiency of Carnot engine |

|
| Entropy |

|
| Inequality of Clausius |

|
Second Law of Thermodynamics
Statement: It is impossible to transfer total heat into work in a cyclic process in the absence of other effect (by Lord Kelvin).
In another way, it is also stated that it is impossible for heat to be transferred by a cyclic process from a body to one which is warmer than itself, without producing other changes
at the same time.
Heat Engines
A machine that can convert heat into work is said to be heat engine.
It is a system that performs the conversion of heat or thermal energy to mechanical work.
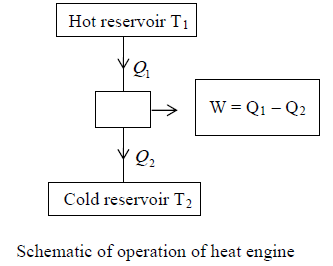
Heat Reservoir
It is an effectively infinite pool of thermal energy at a given constant temperature. Ideally its heat capacity is large enough, that when it is in thermal contact with another system, its temperature remains constant.
All heat engines have mainly three essential components.
- A source: This is a hot region which is a part of the surrounding from which energy flows by heat transfer. Popularly it is known as hot reservoir eg. Nuclear reactor, Furnace, etc.
- The working agent: This under goes change at state as part of a continuous cycle e.g. steam-water.
- A sink: This is respectively a cold region, which is part of the surrounding into which heat is rejected by heat transfer e.g., cooler.
Efficiency of Heat Engine (η):
η = 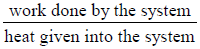
Since, the process is cyclic dU = 0 ⇒dQ = dW
Heat given to system is Q1 and heat rejected by system is Q2 .
η =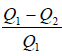
Carnot Cycle
It is theoretical thermodynamic cycle proposed by Nicolas, Leonard Sadi Carnot.
It can be shown that, it is most efficient cycle for converting a given amount of thermal energy into work.
A system undergoing a Carnot cycle is called a Carnot heat engine.
Stages of the Carnot cycle:
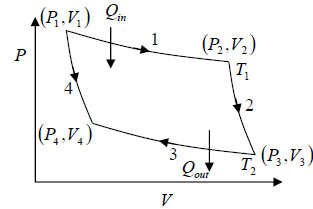
1. Reversible isothermal expansion of the gas at hot temperature, T1 (isothermal heat addition). During this step (1 to 2), the gas is allowed to expand and it does work on the surrounding. The gas expansion is propelled by absorption of Q1 quantity of heat from the high temperature T1 .
2. Reversible adiabatic expansion of the gas. For this step (2 to 3) on figure, the gas
continues to expand i.e., working on surrounding. The gas expansion causes it to cool to
the cold temperature T2 .
3. Reversible isothermal compression of the gas at the low temperature T2 (isothermal heat rejection). The process is shown by 3→4 . Now the surroundings will do work on the gas, causing Q2 quantity of heat to flow out of the gas to the low temperature reservoir.
4. Adiabatic compression of the gas (4 to 1). During this step, the surrounding do work on the gas, compressing it and cause the temperature to rise to T1 . At this point the gas is in the same state as that of the starting at step 1.
Efficiency of Carnot engine
η = W/Q1
W is the work done during cycle and Q1 is heat given to system.
W = W1 + W2 + W3 + W4
W1 = work done during process 1 to 2 for isothermal process = 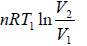
Since, the change in internal energy during the process i.e., dU = 0
Therefore, Q1 = W1 = 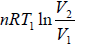 (From first law of thermodynamics)
(From first law of thermodynamics)
W2 is work done during process 2 to 3 in adiabatic process.
Here, dQ = 0 and W2 = 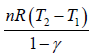
W3 is work done during process 3 to 4 in isothermal compression.
Here, W3 = 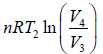
Since, dU = 0 ⇒ Q3 = W3
W4 is the work done during the adiabatic process from 4 to1, is given by
W4 = 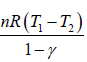
W2 = - W4
W = 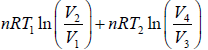
Q1 = 
η = 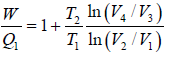 ….(i)
….(i)
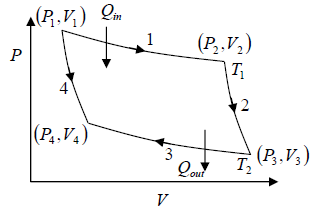
From the figure,
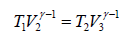 ….(ii)
….(ii)
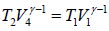 ….(iii)
….(iii)
Dividing equation (ii) by (iii) gives
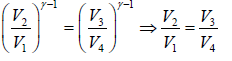 ….(iv)
….(iv)
From equation (i) and (iv)
η = 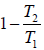 ….(v)
….(v)
For Carnot cycle, 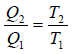
This gives
η = 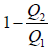 ….(vi)
….(vi)
Example 1: An ideal gas engine operated in a cycle which when represented on a P-V diagram, is a rectangle. If we call P1,P2 as the lower and higher pressures respectively and V1, V2 as lower and higher volume respectively.
(a) Calculate the work done in complete cycle
(b) Indicate in which parts of the cycle heat is absorbed and in which part heat is librated.
(c) Calculate the quantity of heat following into the gas in one cycle
(d) Show that efficiency of the engine is
Work done during process, AB = P2(V2 - V1)
Heat absorbed = nCpΔT
=
=
Since, V2 > V1, so heat is absorbed in the process.
In isochoric process, B-C
WB→C = 0 ⇒ dQ - dU = nCvΔT
=
Since, P1 < P2 , therefore heat is rejected during this process
In isobaric process, C-D
WC→D = P1(V1 - V2)
Heat exchange during the process
Since, V1 < V2, so heat is rejected during this process
In isochoric process, D→A
WD→A = 0
Now, heat exchange during this process is,
Since, P2 > P1 therefore, heat is absorbed.
(a) Work done =
⇒ W =
(b) Heat absorbed during the process A→ B and D→ A is given by
Heat is liberated during the process B→C and C → D is given by
(c) Heat flowing into the cycle is,
Q =
=
=
⇒dQ = dW
(d) Efficiency = W/Qabsorbed =
Therefore, η =
Example 2: An ideal gas is expanded adiabatically from (P1,V1) to (P2,V2). Then it is
compressed isobarically to (P2,V1) . Finally the pressure is increased to P1 at constant
volume V1 .
(a) Show the process in P -V Diagram
(b) Show that the efficiency of the cycle is
(a) The cycle is shown in the figure
The work the system does in the cycle is
W =
Because AB is adiabatic and an ideal gas has the equations
During the CA part of the cycle the gas absorbs heat
Q =
Hence, the efficiency of the engine is
η = W/Q =
Entropy
Entropy is an extensive thermodynamic property that is measure of a system’s thermal energy per unit temperature, which is unavailable for doing useful work. Thermodynamic entropy is a non-conserved state function. For Isolated system, entropy never decreases.
In statistical mechanics, entropy is a measure of the number of ways in which a system may be arranged, often taken to be a measure of ‘disorder’ (the higher the entropy the higher the disorderness).
The infinitesimal change in the entropy (dS) of a system is the infinitesimal transfer of heat energy(∂Q) to a closed system, which is driving a reversible process, divided by temperature (T) of the system.
ΔS = 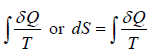
It has unit Joule/Kelvin
Laws of thermodynamics and entropy
According to first law of thermodynamics
∂Q = dU + PdV
From definition of Entropy
ΔS =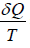 ⇒ ∂Q = TΔS ⇒ TdS
⇒ ∂Q = TΔS ⇒ TdS
which gives, TdS = dU + PdV
Comparative study between P -V diagram and T - S diagram for different process
From first and second law of thermodynamics
As TdS = dU + pdV = CvdT + PdV
dV = 0 for V = constant the slope ⇒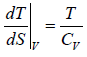
And TdS = dH - VdP
TdS = CpdT -VdP, dP = 0 for P = const) The slope ⇒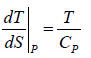
as Cp > Cv ⇒ 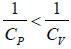
Slope of a constant volume process is more than a constant pressure process,
For Ideal Gas process is given by PVn = C, For different value of n the 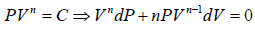 the slope is given by
the slope is given by 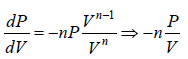
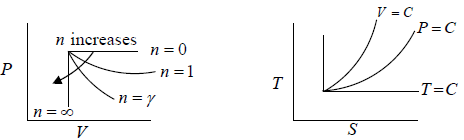
n = 0 P = C Identified as Isobaric process
n = ∞ V = C Identified as Isochoric Process
n =1 T = C Identified as Isothermal Process
n = γ S = C Identified as Adiabatic Process
Inequality of Clausius
Consider an irreversible cyclic engine, working between T1 and T2 . If reversible engine is operating between same temperature, then from Carnot’s theorem.
Efficiency of irreversible engine (ηir) will always be smaller than efficiency of reversible engine(ηr).
ηirr < ηrev
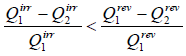
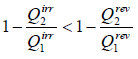
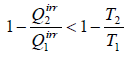
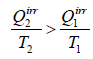
For irreversible cyclic Engine,

or, 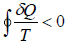
This relation is known as inequality of Clausius.
Example 2: Two Carnot Engines A and B are operated in series. The first one, A receives heat at 900K and rejects to a reservoir at temperature T K . The second engine, B receives the heat rejected by the first engine and then rejects to a heat reservoir at 400K .
Calculate the temperature T for the situation.
(a) The work outputs of the two engines are equal
(b) The efficiency of the two engines are equal.
For Engine A take in heat Q1 at temperature T1 and rejected heat Q at temperature T; and the engine B taken in heat Q at temperature T and reject heat Q2 at temperature T2 .
(a) WA = Q1 - Q and WB = Q - Q2
WA = WB ⇒ Q1 - Q = Q - Q2
⇒
= 2
⇒ T =
= 650 K
(b) ηA = ηB ⇒
=
⇒ T =
= 600 K
Example 3: Calculate the entropy change in isothermal expansion from an initial volume Vi to final volume Vf
For reversible process
TdS = dU + PdV
For isothermal process, dU = 0
⇒T =
= 600 K
As, P =
⇒ dS =
Example 4: A mole of an ideal gas undergoes a reversible isothermal expansion from volume V1 to 2V1 .
(a) What is the change in entropy of the gas?
(b) What is the change in entropy of the universe?
Suppose the same expansion takes place as a free expansion:
(c) What is the change in entropy of the gas?
(d ) What is the change in the entropy of the universe?
(a) In the process of isothermal expansion, the external work done by the system is
W =
Because the internal energy does not change in this process the work is supplied by the heat absorbed from the external world. Thus the increase of entropy of the gas is
ΔS1 =
(b) The change in entropy of the heat source ΔS2 = -ΔS1 thus the total change i entropy of the universe is ΔS = ΔS1 + ΔS2 = 0.
(c) If it is a free expansion, the internal energy of the system is constant. As its final state is the same as for the isothermal process, the change in entropy of the system is also the same as ΔS = R In 2
(d) In this case, the state of the heat source does not change, neither does its entropy.
Therefore the change in entropy of the universe is ΔS = R In 2
Example 5: A mass of liquid at a temperature T1 is mixed with an equal mass of the same liquid at a lower temperature T2. If the system is thermally insulated, then
(a) Compute the entropy-change.
(b) Show that it is necessarily positive.
Let c be the specific heat of the liquid. On mixing equal mass m of the same liquid at temperature T1 and T2 , where T1 > T2.
Let T be the equilibrium temperature of mixture, then
T =
ΔS1 =
, is the entropy change of hotter liquid when cooled fromT1 to T
ΔS1 =
ΔS2 ⇒ Entropy change of cold liquid when heated from T2 to T.
ΔS2 =
ΔS = Entropy change of the system.
ΔS = ΔS1 + ΔS2
=
=
=
(b) We know that arithmetic mean is greater than geometric mean i.e., AM > G.M. So,
∴ ΔS > 0
Example 6: Compute the change in entropy when ice melts into steam. It is given that L1 is latent heat of fusion, c is specific heat of water and L2 is latent heat of vaporization.
Assume T1 be the Kelvin temperature at which ice melts into water and T2 the Kelvin temperature at which water is boiled to steam.
ΔS1 is entropy change when ice is converted into water
ΔS1 =
ΔS2 is entropy change when water is heated from T1 to T2 i.e.,
ΔS2 =
ΔS3 is entropy change when water changes into vapour i.e.,
ΔS3 =
Therefore, total change in entropy, ΔS = ΔS1 + ΔS2 + ΔS3 =
Example 7: A body of constant heat capacity Cp and a temperature Ti is put into contact with a reservoir at temperature Tf. Equilibrium between the body and the reservoir is established at established at constant pressure.
(a) Determined the change in Entropy for Body.
(b) Determined the change in Entropy for Reservoir.
(c) Determine the total entropy change
(a) We assume Ti ≠ Tf (because the change of entropy must be zero when Ti = Tf). The change of entropy of the body is
ΔS1 =
(b) The change of entropy of the heat source is
ΔS2 =
(c) Therefore the total entropy change is
ΔS = ΔS1 + ΔS2 =
when x > 0 and x ≠ 1 the function f(x) = x - 1 - In x > 0.Therefore
ΔS =
Example 8: Water powered machine, A self-contained machine only inputs are two equal steady streams of hot and cold water at temperatures T1 and T2. Its only output is a single high jet of water. The heat capacity per unit mass of water, C , may be assumed to be independent of temperature. The machine is in a steady state and the kinetic energy in the incoming streams is negligible.
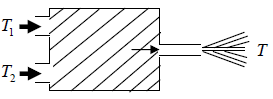
(a) What is the speed of jet in terms of T1,T2 and T, where T is the temperature of water in the jet?
(b) Find the minimum possible temperature T
(c) What is the maximum possible speed of the jet?
(a) The heat intake per unit mass of water is
dQ =
As the machine is in a steady state, v2/2 = ΔQ, giving
v =
(b) Since the entropy increase is always positive, i.e.
ΔS =
(b) We have T ≥
So Tmin =
(c) For maximum speed T must be minimum
Thus,
vmax =
Example 9: Two identical bodies have internal energy U + NCT , with a constant C . The values of and C are the same for each body. The initial temperatures of the bodies are T1 and T2, and they are used as a source of work by connecting them to a Carnot heat engine and bringing them to a common final temperature Tl.
(a) What is the final temperature Tl ?
(b) What is the maximum work delivered?
(a) The bodies attain an equilibrium temperature of T .
T1 > T > T2
as, Cv = dU/dT = NC
Q1 =
Q2 =
W = Q1 - Q2 =
=
ΔS = ΔS1 + ΔS2
=
=
= 0
(b) Conservation of energies gives W =
For maximum work T =
W =
|
6 videos|20 docs|32 tests
|
FAQs on Second Law of Thermodynamics & Entropy - Kinetic Theory & Thermodynamics - Physics
| 1. What is the Second Law of Thermodynamics? |  |
| 2. What are heat engines? |  |
| 3. How is the efficiency of a Carnot engine calculated? |  |
| 4. What is entropy? |  |
| 5. What is the inequality of Clausius? |  |

























 = 2
= 2 = 650 K
= 650 K =
=  ⇒ T =
⇒ T =  = 600 K
= 600 K ⇒ dS =
⇒ dS = 




 , is the entropy change of hotter liquid when cooled fromT1 to T
, is the entropy change of hotter liquid when cooled fromT1 to T

 =
=  =
= 
 ∴ ΔS > 0
∴ ΔS > 0










 So Tmin =
So Tmin = 






 = 0
= 0






















