Second Order Derivative | Mathematics (Maths) for JEE Main & Advanced PDF Download
For understanding the second-order derivative, let us step back a bit and understand what a first derivative is. The first derivative dy/dt represents the rate of the change in y with respect to x. Considering an example, if the distance covered by a car in 10 seconds is 60 meters, then the speed is the first order derivative of the distance travelled with respect to time. Hence, the speed in this case is given as 60/10m/s.
We know that speed also varies and does not remain constant forever. Thus, to measure this rate of change in speed, one can use the second derivative.
Second Order Derivative Definition and Representation
The second-order derivative is nothing but the derivative of the first derivative of the given function. So, the variation in speed of the car can be found out by finding out the second derivative, i.e. the rate of change of speed with respect to time (the second derivative of distance travelled with respect to the time).
Graphically the first derivative represents the slope of the function at a point, and the second derivative describes how the slope changes over the independent variable in the graph. For a function having a variable slope, the second derivative explains the curvature of the given graph.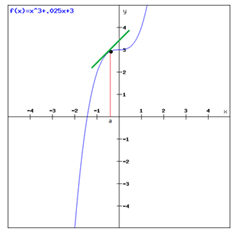
In this graph, the blue line indicates the slope, i.e. the first derivative of the given function. And the second derivative is used to define the nature of the given function. For example, we use the second derivative test to determine the maximum, minimum or the point of inflexion.
Mathematically, if y = f(x)
Then dy/dx = f'(x)
Now if f'(x) is differentiable, then differentiating dy/dx again w.r.t. x we get 2nd order derivative, i.e.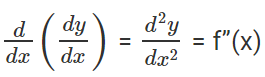
Similarly, higher order derivatives can also be defined in the same way like d3y/dx3 represents a third order derivative, d4y/dx4 represents a fourth order derivative and so on.
Usually, the second derivative of a given function corresponds to the curvature or concavity of the graph. If the second-order derivative value is positive, then the graph of a function is upwardly concave. If the second-order derivative value is negative, then the graph of a function is downwardly open.
As it is already stated that the second derivative of a function determines the local maximum or minimum, inflexion point values. These can be identified with the help of below conditions:
- If f”(x) < 0, then the function f(x) has a local maximum at x.
- If f”(x) > 0, then the function f(x) has a local minimum at x.
- If f”(x) = 0, then it is not possible to conclude anything about the point x, a possible inflexion point.
Second Order Derivative Examples
Let us see an example to get acquainted with second-order derivatives.
Example 1: Find d2y/dx2 if y = e(x3)–3x4
Solution: Given that y = e(x3)–3x4, then differentiating this equation w.r.t. x we get,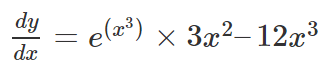
Now to find the 2nd order derivative of the given function, we differentiate the first derivative again w.r.t. x,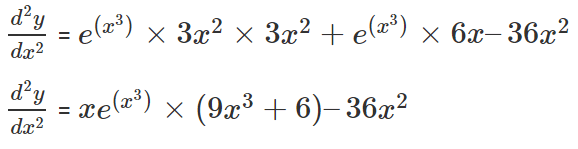
This is the required solution.
Example 2: Find d2x/dx2 if y = 4 sin−1(x2)
Solution: Given that y = 4 sin−1(x2) , then differentiating this equation w.r.t. x we get,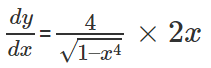
Now for finding the next higher order derivative of the given function, we need to differentiate the first derivative again w.r.t. x,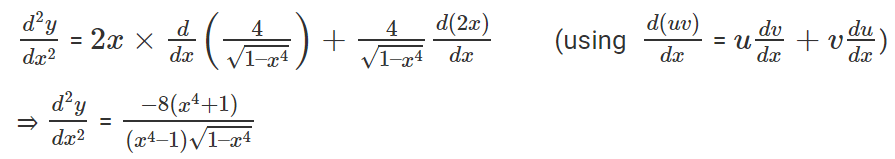
Note: We can also find the second order derivative (or second derivative) of a function f(x) using a single limit using the formula: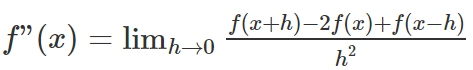
|
172 videos|503 docs|154 tests
|





















