Year 11 Exam > Year 11 Notes > Mathematics for GCSE/IGCSE > Segment Theorems
Segment Theorems | Mathematics for GCSE/IGCSE - Year 11 PDF Download
Circles & Segments
Circle Theorem: Angles at the circumference subtended by the same arc are equal
- This theorem is also sometimes known as the same segment theorem.
- It states that any two angles at the circumference of a circle that are formed from the same two points on the circumference are equal.
- "Subtended" means the equal angles are created by drawing chords from the ends of an arc.
- These chords may or may not pass through the centre. This theorem can be a bit challenging to identify.
- Steps to identify:
- Choose an angle on the circumference and put your index fingers on it.
- Use your fingers to follow the two lines that form the angle to the point where they each meet the circumference.
- See if there are any other lines from these two points that meet at another angle. If so, the two angles are equal.
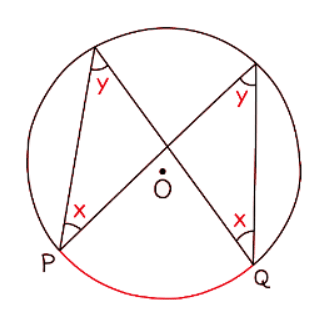
- Remember, angles in the same segment of a circle are equal. In an exam, if you need to cite the same segment theorem, use the key phrase "Angles in the same segment are equal."
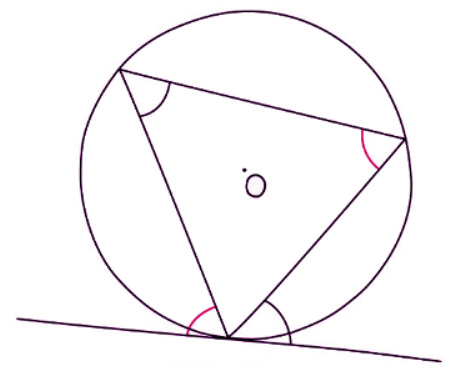
Alternate Segment Theorem
Circle Theorem: Alternate Segment Theorem
- One of the more subtle circle theorems, the Alternate Segment Theorem is a valuable tool for swiftly determining angles in various problems.
- The theorem states that the angle formed between a chord and a tangent is equal to the angle in the alternate segment.
- To recognize this theorem, look for a "cyclic triangle," where all three vertices of a triangle are on the circumference, with one vertex meeting a tangent. Focus on situations where two chords intersect a tangent.
- To identify the equal angles:
- Locate the point where the 'cyclic triangle' intersects the tangent and determine the angle between them.
- Identify the vertex in the triangle opposite to the marked angle at the intersection and mark this angle as equal to the initial angle.
Question for Segment TheoremsTry yourself: What is the theorem that states that angles at the circumference subtended by the same arc are equal?View Solution
The document Segment Theorems | Mathematics for GCSE/IGCSE - Year 11 is a part of the Year 11 Course Mathematics for GCSE/IGCSE.
All you need of Year 11 at this link: Year 11
|
84 videos|120 docs
|
FAQs on Segment Theorems - Mathematics for GCSE/IGCSE - Year 11
| 1. What is the Alternate Segment Theorem? |  |
Ans. The Alternate Segment Theorem states that the angle between a tangent and a chord drawn from the point of contact is equal to the angle in the alternate segment.
| 2. How can the Alternate Segment Theorem be used in solving circle problems? |  |
Ans. The Alternate Segment Theorem can be used to find missing angles in circles when a tangent and a chord are involved by applying the rule that the angle in the alternate segment is equal to the angle between the tangent and the chord.
| 3. What are some key properties of segments in a circle? |  |
Ans. Some key properties of segments in a circle include the fact that the perpendicular from the center of a circle to a chord bisects the chord, and the angle subtended by a chord at the center of a circle is twice the angle subtended at the circumference.
| 4. How can segment theorems be applied to find missing lengths in circles? |  |
Ans. Segment theorems can be used to find missing lengths in circles by applying the properties of segments and angles within the circle, such as using the fact that angles in the same segment are equal or applying the theorem that the angle subtended by a chord at the center is twice the angle at the circumference.
| 5. Are segment theorems applicable only to circles or can they be used in other geometric shapes as well? |  |
Ans. Segment theorems are specific to circles and their properties involving chords, tangents, and segments within the circle. While some concepts may be generalized to other shapes, the specific theorems related to circles are not directly applicable to other geometric shapes.
Related Searches



















