Sequence and Series | Quantitative Aptitude for CA Foundation PDF Download
| Table of contents |

|
| Sequence |

|
| Series |

|
| Arithmetic Progression (A.P.) |

|
| Geometric Progression (G.P.) |

|
| Geometric Mean |

|
| Summary |

|
Sequence
- A sequence refers to an ordered list of items, numbers, letters, symbols, or events that follow a specific pattern or rule.
- The objective is to identify the underlying rule or pattern to predict the next item(s) in the sequence or determine the missing element(s).
Let us consider the following collection of numbers-
(1) 28 , 2, 25, 27, ————————
(2) 2 , 7, 11, 19, 31, 51, —————
(3) 1, 2, 3, 4, 5, 6, ———————
(4) 20, 18, 16, 14, 12, 10, —————
- In (1) the nos. are not arranged in a particular order. In (2) the nos. are in ascending order but they do not obey any rule or law. It is, therefore, not possible to indicate the number next to 51.
- In (3) we find that by adding 1 to any number, we get the next one. Here the number next to 6 is (6 + 1 = ) 7.
- In (4) if we subtract 2 from any number we get the nos. that follows. Here the number next to 10 is (10 –2 =) 8.
- Under these circumstances, we say, the numbers in the collections (1) and (2) do not form sequences whereas the numbers in the collections (3) & (4) form sequences.
- Thus a sequence may be defined as follows:—
An ordered collection of numbers a1, a2, a3, a4, ................., an, ................. is a sequence if according to some definite rule or law, there is a definite value of an, called the term or element of the sequence, corresponding to any value of the natural number n. - Clearly, a1 is the 1st term of the sequence , a2 is the 2nd term, ................., an is the nth term.
- In the nth term an , by putting n = 1, 2 ,3 ,......... successively , we get a1, a2 , a3 , a4, .........
Thus it is clear that the nth term of a sequence is a function of the positive integer n. The nth term is also called the general term of the sequence. To specify a sequence, nth term must be known, otherwise it may lead to confusion. A sequence may be finite or infinite.
1. Finite sequence: If the number of elements in a sequence is finite, the sequence is called finite sequence
2. Infinite sequence: If the number of elements is unending, the sequence is infinite.
A finite sequence a1, a2, a3, a4, ................., an is denoted by 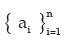 and an infinite sequence a1, a2, a3, a4, ................., an ,................. is denoted by
and an infinite sequence a1, a2, a3, a4, ................., an ,................. is denoted by 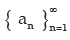 or simply by { an } where an is the nth element of the sequence.
or simply by { an } where an is the nth element of the sequence.
Examples of infinite sequences:
1) The sequence { 1/n } is 1, 1/2, 1/3, 1/4……
2) The sequence { ( – 1 ) n n } is –1, 2, –3, 4, –5,…..
3) The sequence { n } is 1, 2, 3,…
4) The sequence { n / (n + 1) } is 1/2, 2/3, 3/4, 4/5 …….
5) A sequence of even positive integers is 2, 4, 6, .....................................
6) A sequence of odd positive integers is 1, 3, 5, 7, .....................................
Examples of finite sequences:
1) A sequence of even positive integers within 12 i.e., is 2, 4, 6, 10.
2) A sequence of odd positive integers within 11 i.e., is 1, 3, 5, 7, 9. etc.
Series
- An expression of the form a1 + a2 + a3 + ….. + an + ............................ which is the sum of the elements of the sequence { an } is called a series.
- If the series contains a finite number of elements, it is called a finite series, otherwise called an infinite series.
- If Sn = u1 + u2 + u3 + u4 + ……. + un, then Sn is called the sum to n terms(or the sum of the first n terms) of the series and the term sum is denoted by the Greek letter Σ. Thus,
 or simply by Σun.
or simply by Σun.
Examples:
(i) 1 + 3 + 5 + 7 + ............................ is a series in which 1st term = 1, 2nd term = 3 , and so on.
(ii) 2 – 4 + 8 –16 + ..................... is also a series in which 1st term = 2, 2nd term = –4 , and so on.
Arithmetic Progression (A.P.)
- A sequence a1, a2 ,a3, ……, an is called an Arithmetic Progression(A.P.) when a2 – a1 = a3 – a2 = ….. = an – an–1.
- That means A. P. is a sequence in which each term is obtained by adding a constant d to the preceding term.
- This constant ‘d’ is called the common differenceof the A.P.
- If 3 numbers a, b, c are in A.P., we say b – a = c – b or a + c = 2b; b is called the arithmetic mean between a and c.
Examples:
1) 2,5,8,11,14,17,…… is an A.P. in which d = 3 is the common difference.
2) 15,13,11,9,7,5,3,1,–1, is an A.P. in which –2 is the common difference.
Explanation: In (1) 2nd term = 5 , 1st term = 2, 3rd term = 8,
so 2nd term – 1st term = 5 – 2 = 3, 3rd term – 2nd term = 8 – 5 = 3
Here the difference between a term and the preceding term is same that is always constant.
This constant is called common difference.
Now in generel an A.P. series can be written as a, a + d, a + 2d, a + 3d, a + 4d, ……
where ‘a’ is the 1st term and ‘d’ is the common difference.
Thus 1st term ( t1 ) = a = a + ( 1 – 1 ) d
2nd term ( t2 ) = a + d = a + ( 2 – 1 ) d
3rd term (t3) = a + 2d = a + (3 – 1) d
4th term (t4) = a + 3d = a + (4 – 1) d
…………………………………………….
nth term (tn) = a + ( n – 1) d, where n is the position number of the term.
Using this formula we can get
50th term (= t50) = a+ (50 – 1) d = a + 49d
Solved Examples
Example 1: Find the 7th term of the A.P. 8, 5, 2, –1, –4,…..
Sol: Here a = 8, d = 5 – 8 = –3
Now t7 = 8 + (7 – 1) d
= 8 + (7 – 1) (– 3)
= 8 + 6 (– 3)
= 8 – 18
= – 10
Example 2: Which term of the AP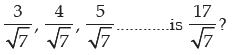
Sol:
We may write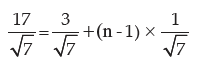
or, 17 = 3 + ( n – 1)
or, n = 17 – 2 = 15
Hence, 15th term of the A.P. is 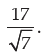
Example 3: If 5th and 12th terms of an A.P. are 14 and 35 respectively, find the A.P.
Sol:Let a be the first term & d be the common difference of A.P.
t5 = a + 4d = 14
t12 = a + 11d = 35
On solving the above two equations,
7d = 21 = i.e., d = 3
and a = 14 – (4 × 3) = 14 – 12 = 2
Hence, the required A.P. is 2, 5, 8, 11, 14,……………
Example 4: Divide 69 into three parts which are in A.P. and are such that the product of the first two parts is 483.
Sol: Given that the three parts are in A.P., let the three parts which are in A.P. be a – d, a, a + d.........
Thus a – d + a + a + d = 69
or 3a = 69
or a = 23
So the three parts are 23 – d, 23, 23 + d
Since the product of first two parts is 483, therefore, we have
23 ( 23 – d ) = 483
or 23 – d = 483 / 23 = 21
or d = 23 – 21 = 2
Hence, the three parts which are in A.P. are
23 – 2 = 21, 23, 23 + 2 = 25
Hence the three parts are 21, 23, 25.
Example 5: Find the arithmetic mean between 4 and 10.
Sol: We know that the A.M. of a & b is = ( a + b ) /2
Hence, The A. M between 4 & 10 = ( 4 + 10 ) /2 = 7
Example 6: Insert 4 arithmetic means between 4 and 324.
4, –, –, –, –, 324
Sol: Here a= 4, d = ? n = 2 + 4 = 6, tn = 324
Now tn = a + ( n – 1 ) d
or 324= 4 + ( 6 – 1 ) d
or 320= 5d i.e., = i.e., d = 320 / 5 = 64
So the 1st AM = 4 + 64 = 68
2nd AM = 68 + 64 = 132
3rd AM = 132 + 64 = 196
4th AM = 196 + 64 = 260
Sum of the first n terms
Let S be the Sum, a be the 1st term and ℓ the last term of an A.P. If the number of term are n,
then tn = ℓ. Let d be the common difference of the A.P.
Now S = a + ( a + d ) + ( a + 2d ) + .. + ( ℓ – 2d ) + ( ℓ – d ) + ℓ
Again S = ℓ + ( ℓ – d ) + ( ℓ – 2d ) + …. + ( a + 2d ) + ( a + d ) + a
On adding the above, we have
2S = ( a + ℓ ) + ( a + ℓ ) + ( a + ℓ ) + …… + ( a + ℓ )
= n( a + ℓ )
or S = n( a + ℓ ) / 2
Note: The above formula may be used to determine the sum of n terms of an A.P. when the
first term a and the last term is given.
Now ℓ = tn = a + ( n – 1 ) d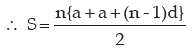
or
Note: The above formula may be used when the first term a, common difference d and the number of terms of an A.P. are given.
Sum of 1st n natural or counting numbers
S = 1 + 2 + 3 + ……. +……. ( n – 2 ) + ( n – 1 ) + n
Again S = n + ( n – 1 ) + ( n – 2 ) + ……… + 3 + 2 + 1
On adding the above, we get
2S = ( n + 1 ) + ( n + 1 ) +....... to n terms
or 2S = n ( n + 1 )
S = n( n + 1 )/2
Then Sum of first, n natural number is n( n + 1 ) / 2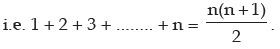
Sum of 1st n odd number
S = 1 + 3 + 5 + …… + ( 2n – 1 )
Sum of first n odd number
S = 1 + 3 + 5 + …… + ( 2n – 1 )
Since S = n{ 2a + ( n –1 ) d } / 2, we find
or S = n2
Then sum of first, n odd numbers is n2, i.e. 1 + 3 + 5 + ..... + ( 2n – 1 ) = n2
Sum of the Squares of the first, n natural nos.
Let S = 12 + 22 + 32 + …… + n2
We know m3 – ( m – 1 )3 = 3m2 – 3m + 1
We put m = 1, 2, 3,……,n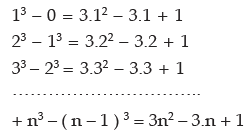
Adding both sides term by term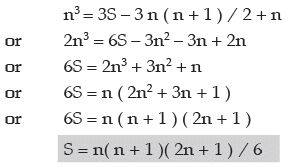
Thus sum of the squares of the first, n natural numbers is 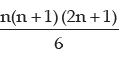
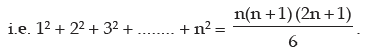
Similarly, sum of the cubes of first n natural number can be found out as 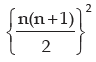
by taking the identity
m4 – ( m – 1 )4 = 4m3 – 6m2 + 4m – 1 and putting m = 1, 2, 3,…., n.
Thus

Geometric Progression (G.P.)
- If in a sequence of terms each term is a constant multiple of the preceding term, then the sequence is called a Geometric Progression (G.P).
- The constant multiplier is called the common ratio.
Examples:
1) In 5, 15, 45, 135,….. common ratio is 15/5 = 3
2) In 1, 1/2, 1/4, 1/9 … common ratio is (1/2) /1 = 1/2
3) In 2, –6, 18, –54, …. common ratio is (–6) / 2 = –3
Illustrations: Consider the following series :–
(i) 1 + 4 + 16 + 64 + …………….
Here second term / first term = 4/1 = 4; third term / second term = 16/4 = 4; fourth term/third term = 64/16 = 4 and so on. Thus, we find that, in the entire series, the ratio of any term and the term preceding it, is a constant.
(ii) 1/3 – 1/9 + 1/27 – 1/81 + ………….
Here second term / 1st term = (–1/9) / ( 1/3) = –1/3
third term / second term = ( 1/27 ) / ( –1/9 ) = –1/3
fourth term / third term = ( –1/81 ) / (1/27 ) = –1/3 and so on.
Here also, in the entire series, the ratio of any term and the term preceding one is constant.
The above-mentioned series are known as Geometric Series.
Let us consider the sequence a, ar, ar2, ar3, ….
1st term = a, 2nd term = ar = ar2–1, 3rd term = ar2 = ar3–1, 4th term = ar3 = ar4 –1, …..
Similarly
nth term of GP tn = arn–1
Thus, common ratio
Thus, general term of a G.P is given by arn–1 and the general form of G.P. is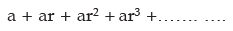
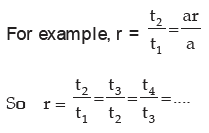
Solved Examples
Example 1: If 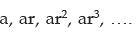 are in G.P. Find the common ratio.
are in G.P. Find the common ratio.
Sol:1st term = a, 2nd term = ar
Ratio of any term to its preceding term = ar/a = r = common ratio.
Example 2: Which term of the progression 1, 2, 4, 8,… is 256?
Sol: a = 1, r = 2/1 = 2, n = ? tn = 256
tn = arn–1
or 256 = 1 × 2n–1 i.e., 28 = 2n–1 or, n – 1 = 8 i.e., n = 9
Thus 9th term of the G. P. is 256
Geometric Mean
- If a, b, c are in G.P we get b/a = c/b => b2 = ac, bis called the geometric mean between a and c.
Example 1: Insert 3 geometric means between 1/9 and 9.
Sol:
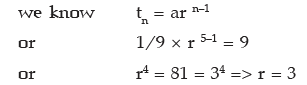
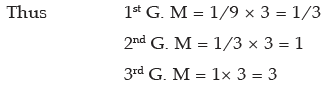
Example 2: Find the G.P where 4th term is 8 and 8th term is 128/625.
Sol: Let a be the 1st term and r be the common ratio.
By the question t4 = 8 and t8 = 128/625
So ar3 = 8 and ar7 = 128 / 625
Therefore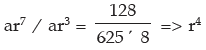
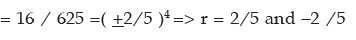
Now, 
Thus the G. P is
125, 50, 20, 8, 16/5, ………..
When r = –2/5 , a = –125 and the G.P is –125, 50, –20, 8, –16/5 ,………
Finally, the G.P. is 125, 50, 20, 8, 16/5, ………..
or, –125, 50, –20, 8, –16/5,………
Sum of first n terms of a G.P.
Let a be the first term and r be the common ratio. So the first n terms are a, ar, ar2, …... arn–1.
If S be the sum of n terms,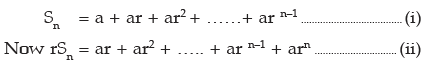
Subtracting (i) from (ii)
or
If r = 1 , then Sn = a + a + a+ ……….. to n terms = na
If the nth term of the G. P be l then 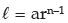
Thus, 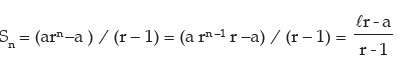
So, when the last term of the G. P is known, we use this formula.
Sum of infinite geometric series
S = a ( 1 – rn ) / (1 – r) when r < 1
= a (1 – 1/Rn) / ( 1 – 1/R ) (since r < 1 , we take r = 1/R).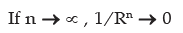
Thus
i.e. Sum of G.P. upto infinity is 
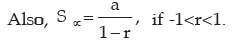
Solved Examples
Example 1: Find the sum of 1 + 2 + 4 + 8 + … to 8 terms.
Sol: Here a = 1, r = 2/1 = 2 , n = 8
Let S = 1 + 2 + 4 + 8 + …… to 8 terms
= 1 ( 28 – 1 ) / ( 2 – 1 ) = 28 – 1 = 255
Example 2: Find the sum to n terms of 6 + 27 + 128 + 629 + …….
Sol: Required Sum = ( 5 + 1 ) + (52 + 2 ) + ( 53 +3 ) + ( 54 + 4 ) + … to n terms
= ( 5 + 52 +53 + …… + 5n ) + ( 1 + 2 + 3 + .. + n terms)
= {5 ( 5n – 1 ) / (5 – 1 )} + {n ( n + 1 ) / 2}
= {5 ( 5n – 1 ) /4} + {n ( n + 1 ) / 2}
Example 3: Find the sum to n terms of the series 3 + 33 + 333 + …….
Sol: Let S denote the required sum.
i.e. S = 3 + 33 + 333 + ………….. to n terms
= 3 (1 + 11 + 111 + ……. to n terms)
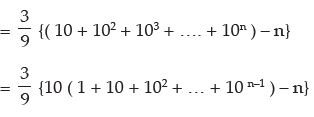
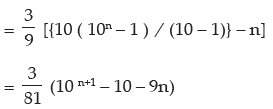
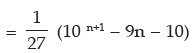
Example 4: Find the sum of n terms of the series 0.7 + 0.77 + 0.777 + …. to n terms.
Sol: Let S denote the required sum.
i.e. S = 0.7 + 0.77 + 0.777 + ….. to n terms
= 7 (0.1 + 0.11 + 0.111 + …. to n terms)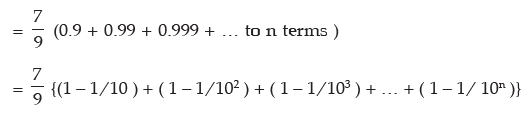
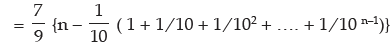
So,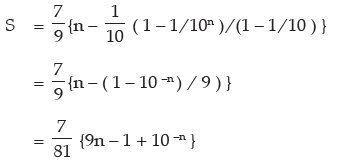
Example 5: Evaluate 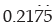 using the sum of an infinite geometric series.
using the sum of an infinite geometric series.
Sol: 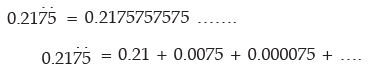
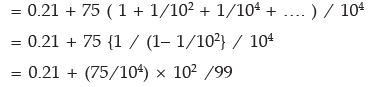

Example 6: Find three numbers in G. P whose sum is 19 and product is 216.
Sol: Let the 3 numbers be a/r, a, ar.
According to the question a/r × a × ar = 216
or a3 = 63 => a =6
So the numbers are 6/r, 6, 6r
Again 6/r + 6 + 6r = 19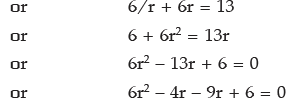

So the numbers are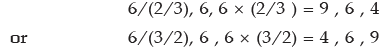
Example 7: A person is employed in a company at ₹3000 per month and he would get an increase of ₹100 per year. Find the total amount which he receives in 25 years and the monthly salary in the last year.
Sol: He gets in the 1st year at the rate of 3000 per month;
In the 2nd year he gets at the rate of ₹ 3100 per month;
In the 3rd year at the rate of ₹ 3200 per month so on.
In the last year the monthly salary will be
₹{3000 + ( 25 – 1 ) × 100} = ₹ 5400
Total amount = 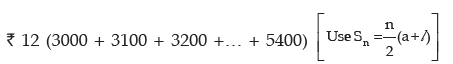
(II) A person borrows ` 8,000 at 2.76% Simple Interest per annum. The principal and the
interest are to be paid in the 10 monthly instalments. If each instalment is double the
preceding one, find the value of the first and the last instalment.
SOLUTION:
Interest to be paid = 2.76 × 10 × 8000 / 100 × 12 = ₹184
Total amount to be paid in 10 monthly instalment is ` (8000 + 184) = ₹8184
The instalments form a G P with common ratio 2 and so ` 8184 = a (210 – 1 ) / ( 2 – 1 ),
a = 1st instalment
Here a = ₹ 8184 / 1023 = ₹ 8
The last instalment = ar10—1 = 8 × 29 = 8 × 512 = ₹4096
Summary
⇒ Sequence: An ordered collection of numbers a1, a2, a3, a4, ................., an, ................. is a sequence if according to some definite rule or law, there is a definite value of an, called the term or element of the sequence, corresponding to any value of the natural number n.
⇒ Series: An expression of the form a1 + a2 + a3 + ….. + an + ............................ which is the sum of the elements of the sequence { an } is called a series. If the series contains a finite number of elements, it is called a finite series, otherwise called an infinite series.
⇒ Arithmetic Progression: A sequence a1, a2 ,a3, ……, an is called an Arithmetic Progression (A.P.) when a2 – a, = a3 – a2 = ….. = an – an–1. That means A. P. is a sequence in which each term is obtained by adding a constant d to the preceding term. This constant ‘d’ is called the common difference of the A.P. If 3 numbers a, b, c are in A.P., we say b – a = c – b or a + c = 2b; b is called the arithmetic mean between a and c.
nth term ( tn ) = a + ( n – 1 ) d,
Where a = First Term
D = Common difference= tn- tn-1
Sum of n terms of AP=
⇒ Sum of the first n terms: Sum of 1st n natural or counting numbers
S = n( n + 1 )/2
Sum of 1st n odd number : S = n2
Sum of the Squares of the first, n natural numbers:
sum of the squares of the first, n natural numbers is
⇒ Geometric Progression (G.P). If in a sequence of terms each term is constant multiple of the proceeding term, then the sequence is called a Geometric Progression (G.P). The constant multiplier is called the common ratio
Sum of first n terms of a G P:
Sum of infinite geometric series
⇒ A.M. of a & b is = ( a + b ) /2
⇒ If a, b, c are in G.P we get b/a = c/b => b2= ac, b is called the geometric mean between a and c.
|
114 videos|164 docs|98 tests
|
FAQs on Sequence and Series - Quantitative Aptitude for CA Foundation
| 1. What is the difference between a sequence and a series? |  |
| 2. How do you identify an arithmetic progression (A.P.)? |  |
| 3. What is the formula for the nth term of an arithmetic progression? |  |
| 4. How is a geometric progression (G.P.) defined? |  |
| 5. What is the geometric mean of two numbers? |  |
|
114 videos|164 docs|98 tests
|

|
Explore Courses for CA Foundation exam
|

|
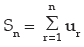 or simply by Σun.
or simply by Σun.

















