Class 10 Maths Chapter 6 Question Answers - Triangles
Q1: If one diagonal of a trapezium divides the other diagonal in the ratio of 1: 2. Prove that one of the parallel sides is double the other.
Sol: Since ABCD is a trapezium,
∴ AB y cΔ ⇒ <1 = <2 and <3 = <4 (Alternate angle)
∴ Δ APB ~ Δ CPD
⇒ ABCD = APCP
But CP : AP = 1 : 2 (Given)
∴ APCP = 21
⇒ ABCD = 21 ⇒ AB = 2 × CD
Q2: In the figure, ABC is a D such that BD ⊥ AC and CE ⊥ AB. Prove that:
PD × BP = PC × EP
Sol: In Δ BEP and Δ CPD,
we have: <BPE = <CPD [Vertically opp. angles]
<BEP = <CDP [Each = 90°]
∴Using AA similarity, we have
Δ BEP ~ Δ CDP
∴Their corresponding sides are proportional,
BPPC = EPPD
BP × PD = EP × PC [By cross multiplication]
Q3: AB is a line segment. PB ⊥ AB and QA ⊥ AB are such that PO = 5 cm and QO = 8 cm. If ar (D POB) = 250 cm2, then find the area of D QOA.
Sol: In Δ QOA and Δ POB,
<QOA = <BOP [Vertically opposite angles]
<QAO = <PBO [Each = 90°]
∴Using AA similarity, we have:
ar (Δ QOA)ar (Δ POB) = (OQ)(OP)²
ar (Δ QOA)250 = (8)(5)²
ar (Δ QOA)250 = 6425
ar (Δ QOA) = 250 × 6425 = 640 cm²
Q4: In the figure, ABCD is a trapezium in which AB y CD. If D BOC ~ D AOD, then prove that AD = BC.
Sol: We have a trapezium ABCD in which AB y DC.
Since Δ BOC ~ Δ AOD [Given]
OBOA = OCOD = BCAD (1)
In Δ ODC and Δ OBA,
∠COD = ∠AOB [Vertically opp. angles]
∠ODC = ∠OBA [Alt. angles]
∴ Using AA similarity, we have:
Δ ODC ~ Δ OBA
ODOB = OCOA ⇒ ODOC = OBOA ...(2)
From (1) and (2):
OBOA = OBOA
⇒ OB × OB = OA × OA
⇒ (OB)² = (OA)²
⇒ OA = OB ...(3)
From (1) to (3), we have:
ADBC = 11
AD = BC
Q5: P and Q are points on the sides of AB and AC respectively of Δ ABC. If AP = 3 cm, PB= 9 cm, AQ = 5 cm, and QC = 15 cm, then show that BC = 4 PQ.
Sol: We have Δ ABC in which P and Q are such that
AP = 3 cm, PB = 9 cm
AQ = 5 cm, QC = 15 cm
APPB = AQQC = 39 = 515 ⇒ 13
i.e., PQ divides AB and AC in the same ratio
∴ PQ || BC
Now, in Δ APQ and Δ ABC:
∠P = ∠B [Corresponding angles]
∠A = ∠A [Common]
∴ Using AA similarity,
Δ APQ ~ Δ ABC
APAB = AQAC = PQBC
312 = 520 = PQBC [∵ AB = 3 + 9 = 12 cm and AC = 5 + 15 = 20 cm]
14 = PQBC
BC = 4PQ
Q6: On one of the longer sides PQ of a rectangle PQRS, a point O is taken such that
SO2 = PO· PQ
Prove that: Δ POS ~ Δ OSR.
Sol:
We have a rectangle PQRS such that
SO2 = PO· PQ
i.e., SO × SO = PO × PQ
SOPO = PQSO
SOPO = SRSO ...(1) [∵ PQ = SR, opp. sides of rectangle PQRS]
Now, in Δ POS and Δ OSR, we have:
POSO = SOSR [∵ SOPO = SRSO in (1)]
<1 = <2 [OE PQ y SR,
opp. sides of a rectangle]
⇒ Using SAS similarity, we have
Δ POS ~ Δ OSR
Q7: Determine the length of the altitude AD of an isosceles D ABC in which AB = AC = 2a cm and BC = a cm.
Sol: We have Δ ABC in AD ⊥ BC and AB = AC = 2a. Also BC = a.
In Δ ADB and Δ ADC
<ADB = <ADC [Each = 90°]
<B = <C [Opp. angles to equal sides of a D]
∴Δ ADB ~ Δ ADC
ADAB = ACAB = DBDC
⇒ DBDC = 1 ⇒ DB = DC = 12a
Now in right Δ ABD, we have:
AB² = AD² + BD²
⇒ AD² = AB² − BD²
⇒ AD² = (AB + BD)(AB − BD)
= (2a + a2) × (2a − a2)
= 5a2 × 3a2 = 154a²
AD = √154a² = a2√15 cm
Q8: In an equilateral triangle with side ‘a’, prove that its area .
Sol: We have Δ ABC such that
AB = BC = AC = a
Let us draw altitude AD ⊥ BC.
In Δ ADC and Δ ADB,
AD = AD [Common]
AC = AB [Each = a]
<ADC = <ADB [Each = 90°]
∴Δ ADC ≌ Δ ADB [RHS congruency]
∴DC = DB
Now, in right Δ ADB,
AB2 = AD2 + DB2
⇒ AD2 = AB2 - DB2
= (AB + DB) (AB - DB)
AD = (a + a2) (a − a2)
= 32 a × 12 a = 34 a²
AD = √34 a² = √32 a
Now, area of Δ ABC = 1/2 × Base × Altitude
= 12 × BC × AD
= 12 × a × √32 a
= √34 a² square units
Thus, the area of an equilateral triangle = √34 a².
Q9: In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Sol: We have Δ ABC in which AB = AC = CA and an altitude AD ⊥ BC.
In Δ ADB and Δ ADC
<ADB = <ADC [Each = 90°]
AB = AB [Given]
AD = AD [Common]
Using RHS congruency, we have
< ADB ≌ < ADC
⇒ DB = DC = 12 BC ...(1)
Now, in right Δ ADB, we have:
AB² = AD² + BD² [Using Pythagoras Theorem]
AB² = AD² + [12 BC]²
[∵ BD = 12 BC, from (1)]
AB² = AD² + 14 BC²
⇒ AB² − 14 BC² = AD²
4 AB² − AB²4 = AD²
⇒ 34 AB² = AD²
⇒ 3 AB² = 4 AD²
⇒ 3 [Side of the equilateral triangle]
= 4 [Altitude]2.
Q10: ABC is a right triangle in which <C = 90° and CD ⊥ AB. If BC = a, CA = b, AB = c and CD = p, then prove that:
=1p² = 1a² + 1b². Sol: We have a right Δ ABC such that ∠C = 90°.
Also, CD ⊥ AB
Now, ar (Δ ABC) = 12 × Base × Height
= 12 × BC × AC
= 12 × a × b ...(1)
Also, ar (Δ ABC) = 12 × AB × CD ... (2)
From (1) and (2), we have:
12 ab = 12 cp
⇒ ab = cp
Dividing throughout by abp, we have:
ababp = cpabp
1p = cab
Squaring both sides:
1p² = c²a²b² ...(3)
Now, in right Δ ABC,
AB² = AC² + BC²
⇒ c² = b² + a² ...(4)
∴ From (3) and (4), we get:
1p² = b² + a²a²b²
= b²a²b² + a²a²b²
= 1a² + 1b²
Thus, 1p² = 1a² + 1b².
Q11: ABC is a right triangle, right-angled at A, and D is the mid-point of AB. Prove that
BC2 = CD2 + 3 BD2. 
Sol: We have a right Δ ABC in which <A = 90°
∴Using Pythagoras Theorem, we have:
BC2 = AB2 + AC2 ...(1)
Again, Δ ACD is right D, <A = 90°
∴CD2 = AD2 + AC2...(2) [Using Pythagoras Theorem]
Subtracting (2) from (1), we get
BC2 - CD2 = AB2 - AD2 ...(3)
Since D is the mid-point of AB
∴2 BD = AB and AD = BD ...(4)
From (3) and (4), we have:
∴BC2 - CD2 = (2 BD)2 - (BD)2
= 4 BD2 - BD2
BC2 = CD2 + 3 BD2
Q12: In the figure, O is any point inside a rectangle ABCD such that OB = 6 cm, OD = 8 cm, and OA = 5 cm. Find the length of OC. 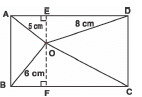
Sol: Let us draw EOF y AB ⇒ OE ⊥ AD and OF ⊥ BC
In Δ OFB, Œ <F = 90°
∴Using Pythagoras theorem, we have:
CB2 = OF2 + BF2 ...(1)
In Δ OED, <E = 90°
∴Using Pythagoras theorem, we have:
OD2 = OE2 + DE2 ...(2)
Adding (1) and (2), we get
OB2 + OD2 = OF2 + BF2 + OE2 + DE2
= OF2 + AE2 + OE2 + CF2 [ΠBF = AE and CF = DE]
= (OF2 + CF2) + (OE2 + AE2)
= OC2 + OA2
= OC2 + 52
⇒ 62 + 82 = OC2 + 52
⇒ 36 + 64 = OC2 + 25
⇒ OC2 = 36 + 64 - 25 = 75
⇒ OC = √75 − √(25 × 3) − √(3 × 5)
OC = 5√3 cm
Thus OC = 5√3cm.
Q13: In the figure, if AD ⊥ Bc, then prove that:
AB2 + CD2 = AC2 + BD2 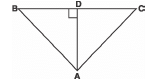
Sol: In D ADC, <ADC = 90°
∴ AD2 = AC2 - CD2 .....(1) (Using Pythagoras Theorem)
Similarly, in D AbD,
⇒ AD2 = AB2 - DB2.....(2)
From (1) and (2), we have
AB2 - DB2 = AC2 - CD2
⇒ AB2 + CD2 = AC2 + BD2
Q14: In the given figure, AD ⊥ BC and BD = CD. Prove that:
CA² = AB² + 12 BC²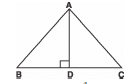
Sol: BD = 1/2 CD
∴ 3 BD = CD
Since BD + DC = BC
∴ BD + 3 BD = BC
⇒ 4 BD = BC
⇒ BD = 1/4 BC
⇒ CD = 3/4 BC
Now, in right Δ ADC, < D = 90°
By Pythagoras theorem, we get
CA2 = AD2 + CD2 ...(1)
Also in the right Δ ADB
AD2 = AB2 - BD2 ...(2)
From (1) and (2),
CA2 = AB2 - BD2+ CD2
= AB² − (14 BC)² + (34 BC)²
= AB² − BC²16 + 9 BC²16
= AB² + 816 BC²
= AB² + 12 BC²
Thus, CA² = AB² + 12 BC²
Q15: In the given figure, M is the mid-point of the side CD of parallelogram ABCD. The line BM is drawn intersecting AC at L, and AD produces D at E. Prove that EL = 2 BL.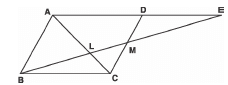
So: We have parallelogram ABCD in which M is the midpoint of CD.
In Δ EMD and Δ BMC
MD = MC [ΠM is mid-point of CD]
<EMD = <CMB [Vertically opposite angles]
<MED = <MBC [Alternate interior angles]
∴ Δ BMC ≌ Δ EMD [AAS congruency]
⇒ BC = ED ⇒ AD = ED ...(1)
[ΠBC = AD, opposite sides of parallelogram]
Now, in Δ AEL and Δ CBL
<AEL = <CBL [Alternate interior angles]
<ALE = <CLB [Vertically opposite angles]
∴ By AA similarity, we have:
ELBL = AEBC = AD + DEBC
= BC + BCBC [From (1)]
= 2 BCBC − 2
⇒ ELBL = 2 ⇒ EL = 2 BL
Q16. In the given figure, Δ ABC is right-angled at C and DE ^ AB. Prove that Δ ABC ~ Δ ADE and hence find the length of AE and DE.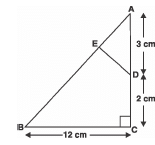
Sol: In Δ ABC and Δ ADE, we have:
<A = <A [Common]
<C = <E [Each = 90°]
∴ Δ ABC ~ Δ ADE [AA Similarity]
ABAD = BCDE = ACAE ...(1)
In right Δ ABC, ∠C = 90°
Using Pythagoras theorem, we have:
AB² = BC² + AC²
= 122 + 52
= 144 + 25 = 169
⇒ AB = √169 = 13 cm
Now, from (1), we get:
133 = 12DE = 5AE
⇒ DE12 = 12 × 313 = 2.77 cm
And
AE5 = 5 × 313 = 1.15 cm
⇒ DE = 2.77 cm and AE = 1.15 cm
Q17: In the given figure, DEFG is a square and <BAC = 90°. Show that DE2 = BD × EC.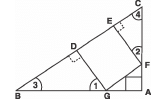
Sol: In Δ DBG and Δ ECF
<3 + <1 = 90° = <3 + <4
∴<3 + <1 = <3 + <4
⇒ <1 = <4
<D = E = 90°
∴Using AA similarity, we have:
= BDDG = EFEC
⇒BD × EC = EF × DG But DG = EF = DE
∴BD × EC = DE × DE
⇒ BD × EC = DE2
Thus, DE2 = BD × EC
Q18: In the figure, AD ⊥ BC and BD = CD. Prove that 2 CA2 = 2 AB2 + BC2. 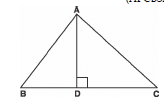
Sol: ΠBD = 1/3 CD
⇒ 3 BD = CD
∴BC = BD + DC
⇒ BC = BD + 3 BD
⇒ BC = 4 BD ...(1)
And BD = 14 BC and DC = 3 BD = 34 BC ...(4)
In right Δ ADC, Using Pythagoras theorem,
CA² = AD² + DC²
AD² + (34 BC)² [From (4)]
In right Δ ADB, Using Pythagoras theorem,
AD² = AB² − BD²
= AB² − [14 BC]²
= AB² − BC²16
CA² = (AB² − BC²16) + (34 BC)²
= AB² − BC²16 + 916 BC²
= AB² + 12 BC²
CA² = 2 AB² + BC²
Q19: If the diagonals of a quadrilateral divide each other proportionally, prove that it is a trapezium.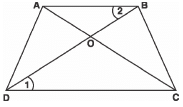
Sol: We have a quadrilateral ABCD such that its diagonals intersect at O and
OAOC = OBOD
∠AOB = ∠COD
<AOB = <COD [Vertically opposite angles]
∴ Using SAS similarity, we have
Δ AOB ~ Δ COD
⇒ Their corresponding angles are equal i.e., <1 = <2
But they form a pair of int. alt. angles.
⇒ AB y DC
⇒ ABCD is a trapezium.
Q20: Two triangles ABC and DBC are on the same base BC and on the same side of BC in which
<A = <D = 90°. If CA and BD meet each other at E, show that
AE· EC = BE· ED
Sol: We have right Δ ABC and right Δ DBC on the same base BC such that
<A = <D = 90°
In Δ ABE and Δ DCE
<A = <D = 90°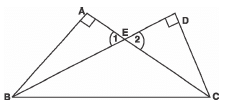
<1 = <2 [Vertically opp. angles]
∴ Using AA similarity, we have:
Δ ABE ~ Δ DCE
⇒ Their corresponding sides are proportional.
⇒ AEED = BEEC
AE.EC = BE.ED
Q21: E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that
Δ ABE ~ Δ CFB
Sol: We have parallelogram ABCD
In Δ ABE and Δ CFB, we have
<A = <C [Opposite angles of parallelogram]
<AEB = <EBC [Alternate angles, AD y BC]
∴ Using AA similarity, we get
Δ ABE ~ Δ CFB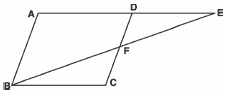
Q22: In Δ ABC, if AD is the median, then show that AB2 + AC2 = 2 [AD2 + BD2]. 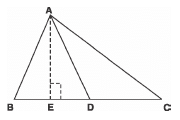
Sol: AD is a median,
∴ BD = DC
Let us draw AE ≌ BC
Now, in rt. Δs AEB and AEC, we have
AB2 = BE2 + AE2 ...(1)
AC2 = CE2 + AE2 ...(2)
Adding (1) and (2),
AB2 + AC2 = BE2 + AE2 + CE2 + AE2
= (BD - ED)2 + AE2 + (CD + DE)2 + AE2
= 2AE2 + 2ED2 + BD2 + CD2
= 2 [AE2 + ED2] + BD2 + BD2 [BD = CD]
= 2 [AD]2 + 2BD2 [AE2 + ED2 = AD2]
= 2 [AD2 + BD2]
Thus, AB2 + AC2 = 2 [AD2 + BD2]
Q23: Triangle ABC is right-angled at B and D is the midpoint of BC. Prove that:
AC2 = 4 AD2 - 3 AB2
Sol: D is the mid-point of BC.
∴ BC = 2 BD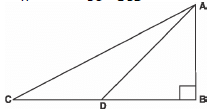 Now, in Δ ABC, AC2 = BC2 + AB2
Now, in Δ ABC, AC2 = BC2 + AB2
= (2 BD)2 + AB2
= 4 BD2 + AB2 ...(1)
In the right Δ ABD,
Using Pythagoras theorem,
AD2 = AB2 + BD2
⇒ BD2 = AD2 - AB2 ...(2)*
From (1) and (2), we get
AC2 = 4 [AD2 - AB2] + AB2
⇒ AC2 = - 4 AB2 + 4 AD2 + AB2
⇒ AC2 = - 3 AB2 + 4 AD2
or AC2 = 4 AD2 - 3 AB2
|
127 videos|551 docs|75 tests
|
FAQs on Class 10 Maths Chapter 6 Question Answers - Triangles
| 1. What are the different types of triangles based on their sides? |  |
| 2. How can you determine the area of a triangle? |  |
| 3. What is the Pythagorean theorem and how does it relate to triangles? |  |
| 4. How do you find the perimeter of a triangle? |  |
| 5. What is the significance of the angles in triangles? |  |






















