Class 9 Maths Chapter 4 Question Answers - Linear Equations in Two Variables

Clear all your Class 9 doubts with EduRev Join for Free

Join for Free

Q1: Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
(i) x – y/5 – 10 = 0
(ii) -2x+3y = 6
(iii) y – 2 = 0
Sol:
(i) x – y/5 – 10 = 0
The equation x-y/5-10 = 0 can be written as:
(1)x + (-1/5) y + (-10) = 0
Now compare the above equation with ax + by + c = 0
Thus, we get;
a = 1
b = -⅕
c = -10

(ii) -2x + 3y = 6
Re-arranging the given equation, we get,
–2x + 3y – 6 = 0
The equation –2x + 3y – 6 = 0 can be written as,
(–2)x + 3y +(– 6) = 0
Now comparing (–2)x + 3y +(– 6) = 0 with ax + by + c = 0
We get, a = –2
b = 3
c = -6

(iii) y – 2 = 0
The equation y – 2 = 0 can be written as,
0x + 1y + (–2) = 0
Now comparing 0x + 1y + (–2) = 0with ax + by + c = 0
We get, a = 0
b = 1
c = –2

Q2: Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k.
Sol:
The given equation is
2x + 3y = k
According to the question, x = 2 and y = 1.
Now, Substituting the values of x and y in the equation 2x + 3y = k,
We get,
⇒ (2 x 2)+ (3 × 1) = k
⇒ 4+3 = k
⇒ 7 = k
⇒ k = 7
The value of k, if x = 2, y = 1 is a solution of the equation 2x + 3y = k, is 7.

Q3: If the point (3, 4) lies on the graph of the equation 3y = ax + 7, find the value of a.
Sol:
The given equation is
3y = ax + 7
According to the question, x = 3 and y = 4
Now, Substituting the values of x and y in the equation 3y = ax + 7,
We get,
(3×4) = (ax3) + 7
⇒ 12 = 3a+7
⇒ 3a = 12–7
⇒ 3a = 5
⇒ a = 5/3
The value of a, if the point (3, 4) lies on the graph of the equation 3y = ax + 7 is 5/3.

Q4: Draw the graph of the linear equation 3x + 4y = 6. At what points, the graph cuts X and Y-axis?
Sol: Given equation,
3x + 4y = 6.
We need at least 2 points on the graph to draw the graph of this equation,
Thus, the points the graph cuts
(i) x-axis
Since the point is on the x-axis, we have y = 0.
Substituting y = 0 in the equation, 3x + 4y = 6,
We get,
3x + 4×0 = 6
⇒ 3x = 6
⇒ x = 2
Hence, the point at which the graph cuts x-axis = (2, 0).

(ii) y-axis
Since the point is on the y-axis, we have, x = 0.
Substituting x = 0 in the equation, 3x + 4y = 6,
We get,
3×0 + 4y = 6
⇒ 4y = 6
⇒ y = 6/4
⇒ y = 3/2
⇒ y = 1.5
Hence, the point at which the graph cuts y-axis = (0, 1.5).
Plotting the points (0, 1.5) and (2, 0) on the graph.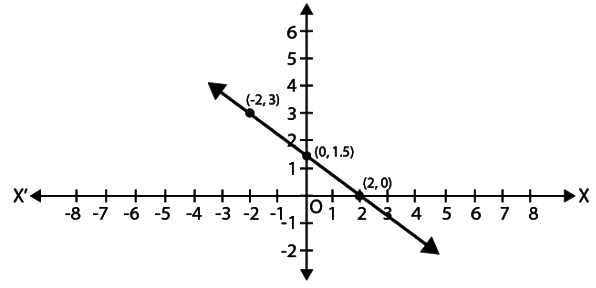

Q5: Write four solutions for each of the following equations:
(i) 2x + y = 7
(ii) πx + y = 9
Sol: (i) 2x + y = 7
To find the four solutions of 2x + y = 7 we substitute different values for x and y
Let x = 0
Then,
2x + y = 7
(2×0)+y = 7
y = 7
(0,7)
Let x = 1
Then,
2x + y = 7
(2×1)+y = 7
2+y = 7
y = 7 – 2
y = 5
(1,5)
Let y = 1
Then,
2x + y = 7
2x+ 1 = 7
2x = 7 – 1
2x = 6
x = 3
(3,1)
Let x = 2
Then,
2x + y = 7
2(2)+y = 7
4+y = 7
y = 7 – 4
y = 3
(2,3)
The solutions are (0, 7), (1,5), (3,1), (2,3)

(ii) πx + y = 9
To find the four solutions of πx + y = 9 we substitute different values for x and y
Let x = 0
Then,
πx + y = 9
(π × 0)+y = 9
y = 9
(0,9)
Let x = 1
Then,
πx + y = 9
(π×1)+y = 9
π+y = 9
y = 9-π
(1,9-π)
Let y = 0
Then,
πx + y = 9
πx +0 = 9
πx = 9
x =9/π
(9/π,0)
Let x = -1
Then,
πx + y = 9
(π(-1))+y = 9
-π + y = 9
y = 9+π
(-1,9+π)
The solutions are (0,9), (1,9-π),(9/π,0),(-1,9+π)

Q6: Draw the graph of each of the following linear equations in two variables:
(i)y = 3x
(ii) 3 = 2x + y
Sol: (i) y = 3x
To draw a graph of linear equations in two variables, let us find out the points to plot.
To find out the points, we have to find the values for which x and y satisfies the given equation.
Here,
y=3x
Substituting the values for x,
When x = 0,
y = 3x
y = 3(0)
⇒ y = 0
When x = 1,
y = 3x
y = 3(1)
⇒ y = 3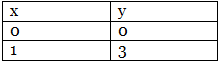
The points to be plotted are (0, 0) and (1, 3)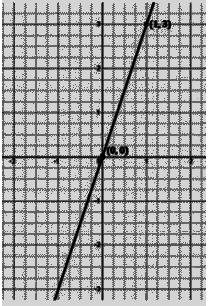

(ii) 3 = 2x + y
To draw a graph of linear equations in two variables, let us find out the points to plot.
To find out the points, we have to find the values for which x and y satisfies the given equation.
Here,
3 = 2x + y
Substituting the values for x,
When x = 0,
3 = 2x + y
⇒ 3 = 2(0) + y
⇒ 3 = 0 + y
⇒ y = 3
When x = 1,
3 = 2x + y
⇒ 3 = 2(1) + y
⇒ 3 = 2 + y
⇒ y = 3 – 2
⇒ y = 1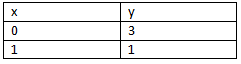
The points to be plotted are (0, 3) and (1, 1)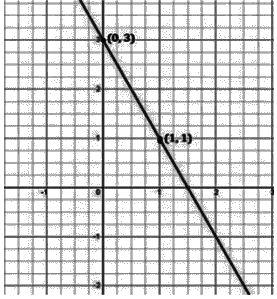

Q7: Show that the points A (1, 2), B ( – 1, – 16) and C (0, – 7) lie on the graph of the linear equation y = 9x – 7.
Sol:
We have the equation,
y = 9x – 7
For A (1, 2),
Substituting (x,y) = (1, 2),
We get,
2 = 9(1) – 7
2 = 9 – 7
2 = 2
For B (–1, –16),
Substituting (x,y) = (–1, –16),
We get,
–16 = 9(–1) – 7
-16 = – 9 – 7
-16 = – 16
For C (0, –7),
Substituting (x,y) = (0, –7),
We get,
– 7 = 9(0) – 7
-7 = 0 – 7
-7 = – 7
Hence, the points A (1, 2), B (–1, –16) and C (0, –7) satisfy the line y = 9x – 7.
Thus, A (1, 2), B (–1, –16) and C (0, –7) are solutions of the linear equation y = 9x – 7
Therefore, the points A (1, 2), B (–1, –16), C (0, –7) lie on the graph of linear equation y = 9x – 7.