Linear Equations in Two Variables Class 9 Notes Maths Chapter 4
- In a plane, a point can be located using two mutually perpendicular lines such that one of them is horizontal and the other vertical.
- The horizontal line is called the x-axis and the vertical line is called the y-axis.
- An equation of the form ax + by + c = 0, where ‘a’, ‘b’ and ‘c’ are real numbers such that ‘a’ and ‘b’ are not both zero, is called a linear equation.
- There can be an infinite number of solutions of a linear equation.
- The graph of a linear equation in two variables is a straight line.
- Every point on the graph of a linear equation in two variables is a solution of the linear equation. On the other hand, every solution of a linear equation is a point of the graph of the linear equation.
- The graph of x = 0 is the y-axis itself.
- The graph of y = 0 is the x-axis itself.
- An equation of the type y = mx represents a line passing through the origin.
Linear Equations
An equation in two variables ‘x’ and ‘y’ in form of ax + by + c = 0 is called a linear equation. Such that a, b and c are real numbers.
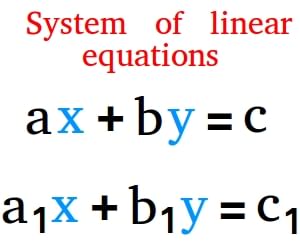 Linear equation If we draw the graph of a degree one equation in two variables, we get a straight line.Every point on the graph of a linear equation is its solution. On the other hand, a solution of a linear equation always lies on the straight line representing the linear equation. Let us check that the point (2, 3) lies on the graph of 3x – 4y + 6 = 0.
Linear equation If we draw the graph of a degree one equation in two variables, we get a straight line.Every point on the graph of a linear equation is its solution. On the other hand, a solution of a linear equation always lies on the straight line representing the linear equation. Let us check that the point (2, 3) lies on the graph of 3x – 4y + 6 = 0.
We know that (2, 3) means x = 2 and y = 3,
L.H.S. = 3x – 4y + 6
= 3 x (2) – 4 x (3) + 6
= 6 – 12 + 6
= 12 – 12
= 0
= R.H.S.
Since L.H.S. = R.H.S. i.e. (2, 3) satisfy the equation 3x – 4y + 6 = 0.
Solution of Linear Equation in Two Variables
A linear equation involves two variables x and y. By solution of a linear equation, we mean a pair of values, one for x and another for y which satisfy the given equation.
Note:
I. We write the solution of a linear equation as an ordered pair such that the first value for ‘x’ and then the value for ‘y’.
II. There is no end to different pairs of solution of a linear equation in two variables (i.e. a linear equation in two variables has infinitely many solutions).
Graph of Linear Equations in Two Variables
We know that a ‘degree one’ polynomial in two variables has many solutions. These solutions are presented in the form of ordered pairs as (x, y). If we plot these ordered pairs on a graph paper and join them, we get a straight line.
Note: A ‘degree one’ polynomial equation ax + by + c = 0 is called a linear equation because its geometrical representation is a straight line.
To draw a graph of a linear equation of the form ax + by + c = 0, we take the followingsteps:
I. Express ‘y’ in terms of x.
II. Choose at least two or three values of x and find the corresponding values of y, satisfying the given equation.
III. Write these values of x and y in the form of a table.
IV. Plot the above-ordered pairs (x, y) on graph paper.
V. Joining these points, we get a straight line. This line is the required graph of the given equation.
Remember
I. Every point whose coordinates satisfy the given equation lies on the line.
II. Every point (l, m) on the line (the graph of the given equation) gives a solution x = l and y = m.
III. If a point does not lie on the graph line, it is not a solution of the equation.
Equations of Lines parallel to the x-axis and y-axis
I. Equation of the x-axis is y = 0.
II. Equation of the y-axis is x = 0.
III. Equation of a line parallel to the y-axis at a distance ‘m’ from it is x = 0 + m or x = m.
IV. Equation of a line parallel to the x-axis at a distance ‘n’ from it is y = 0 + n or y = n.
|
40 videos|566 docs|57 tests
|
FAQs on Linear Equations in Two Variables Class 9 Notes Maths Chapter 4
| 1. What is the general form of a linear equation in two variables? |  |
| 2. How do you identify a line parallel to the x-axis? |  |
| 3. What is the equation of a line parallel to the y-axis? |  |
| 4. How do you graph a linear equation in two variables? |  |
| 5. What is the significance of the slope in a linear equation? |  |






















