Polynomials Class 9 Notes Maths Chapter 2
| Table of contents |

|
| Polynomial |

|
| Algebraic Identities |

|
| Variable |

|
| Constant |

|
| Algebraic Expression |

|
Polynomial
- An algebraic expression, in which the variables involved have only whole number powers, is called a polynomial.
- Polynomials of degree 1, 2 and 3 are called linear, quadratic and cubic polynomials respectively.
- Polynomials containing one, two and three non-zero terms are called monomial, binomial and trinomial respectively.
- If f(x) be a polynomial of degree n ≥ 1 and let ‘a’ be any real number, then f(a) is the remainder for ‘f(x) being divided by (x – a)’.
- Let f(x) be a polynomial of degree n ≥ 1, then (x – a) is a factor of f(x) provided f(a) = 0. Also if (x + a) is a factor of f(x), then f(–a) = 0
Algebraic Identities
Algebraic identities are equations that hold true for all values of the variables involved. They are fundamental tools in algebra, simplifying expressions and solving equations. Below are some key algebraic identities:
Difference of Cubes:
x3 - y3 = (x - y)(x2 + xy + y2)
Sum of Cubes:
x3 + y3 = (x + y)(x2 - xy + y2)
Sum of Three Cubes:
If x + y + z = 0, then:
x3 + y3 + z3 = 3xyz.
Otherwise,
x3 + y3 + z3 - 3xyz = (x + y + z)(x2 + y2 + z2 - xy - yz - zx)
Square of a Trinomial:
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
Expansion of a Binomial Cube:
(x + y)3 = x3 + y3 + 3xy(x + y)
Difference of a Binomial Cube:
(x - y)3 = x3 - y3 - 3xy(x - y)
These identities are invaluable for simplifying complex algebraic expressions and solving polynomial equations efficiently.
Variable
A symbol that can be assigned different numerical values is known as a variable. Variables are generally denoted by x, y, z, p, q, r, s, etc.
Constant
A symbol having a fixed value is called a constant, e.g. 8, 5, 9, p, a, b, c, etc. are constants.
Note: The values of constants remain the same throughout a particular situation, but the value of a variable can keep changing.
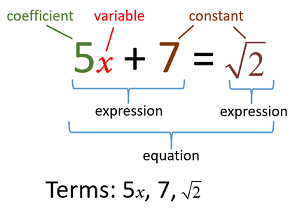
Algebraic Expression
An algebraic expression is a combination of constants and variables connected using one or more of the basic operations: addition (+), subtraction (–), multiplication (×), and division. For example, 3a + 5 is an algebraic expression.Example:  is an algebraic expression.
is an algebraic expression.
Terms
Various parts of an algebraic expression separated by (+) or (–) operations are called terms.
Examples: (i) In the above algebraic expression, terms are 7, 8x, –6x2y and 
(ii) Various terms of 3p4 – 6q2 + 8r3s – 2pq + 6s3 are: 3p4, –6q2, 8r3s, –2pq and 6s3
 Algebraic Expression
Algebraic Expression
Polynomial
An algebraic expression in which the variables involved have non-negative integral powers is called a polynomial.
Examples: (i) x3 + x2 – 4x – 7;
(ii) 3p3 + 5p – 9;
(iii) x2 + 2x; etc. are all polynomials
Note: I. Each variable in a polynomial has a whole number as its exponent.
II. Each term of a polynomial has a coefficient.
Degree of a Polynomial
I. In the case of a polynomial involving one variable, the highest power of the variable is called the degree of the polynomial.
Example: The degree of x5 – 2x3 + x is 5.
II. In the case of a polynomial involving more than one variable, the highest sum of exponents of variables in any term is called the degree of the polynomial.
Example: The degree of p2 – 6p6q + 5p2q3 – 3q4 is 7
(∵ The term –p6q has the sum of exponents of p and q as 6 + 1, i.e. 7)
Types of Polynomials
A [On the basis of the number of terms]
(i) Monomial: A polynomial containing only one non-zero term is called a monomial, such as 5x2 or 3.
(ii) Binomial: A polynomial containing two non-zero terms is called a binomial, x + 2 or 4x3 + 1.
(iii) Trinomial: A polynomial containing three non-zero terms is called a trinomial, such as x2 + x + 1.
Note: I. A monomial containing a constant only is called a constant polynomial.
II. A monomial containing its term as zero only is called a zero polynomial.
III. If we add polynomials, we get a polynomial.
IV. If we multiply polynomials, we get a polynomial.
B [On the basis of its degree]
(i) Linear Polynomial: A polynomial of degree 1 is called a linear polynomial, such as ax + b.
(ii) Quadratic Polynomial: A polynomial of degree 2 is called a quadratic polynomial, such as ax2 + bx + c.
(iii) Cubic Polynomial: A polynomial of degree 3 is called a cubic polynomial, such as ax3 + bx2 + cx + d.
(iv ) Biquadratic Polynomial: A polynomial of degree 4 is called a biquadratic polynomial, such as ax4 + bx3 + cx2 + dx + e.
|
40 videos|420 docs|51 tests
|
FAQs on Polynomials Class 9 Notes Maths Chapter 2
| 1. What is a polynomial in mathematics? |  |
| 2. How can you identify the degree of a polynomial? |  |
| 3. What are the different types of polynomials based on their degree? |  |
| 4. Can a polynomial have negative exponents or fractions as coefficients? |  |
| 5. How do you perform addition and subtraction of polynomials? |  |






















