Class 7 Maths Chapter 10 Question Answers - Algebraic Expressions
Q1. Add x + y − 5, y − x + 5, x − y + 5
Ans: Adding the coefficients of the similar terms will give the sum of three terms that is,

Q2. Add 3a2b2 − 4ab + 5, 8a2b2 + 12ab − 9, 15 − 6ab − 5a2b2.
Ans: Adding the coefficients of the similar terms will give the sum of three terms that is,

Q3. Subtract -x2 + 6xy from 8x2 - 4xy + 12.
Ans: Subtracting the coefficients of the similar terms will give the difference of two terms that is,

Q4. Subtract a2 − 4b2 + 3ab − 20 from 2a2 + 6b2 + 7ab + 12.
Ans: Subtracting the coefficients of the similar terms will give the difference of two terms that is,

Q5. Find the value of the given equation 4x2 − 3x + 12, if x = −3
Ans: We are given the quadratic equation of x as,
4x2 − 3x + 12
Substituting the value x = −3,
= 4(−3)2 − 3(−3) + 12
=4 × 9 + 9 + 12
=36 + 9 + 12
=57
Q6. Simplify 3(2x + 1) + 4x + 15 when x = −1.
Ans: We are given the quadratic equation of x as,
3(2x + 1) + 4x + 15
Substituting x = −1,
= 3[2(−1) + 1] + 4(−1) + 15
= 3(−2 + 1)−4 + 15
= −3−4 + 15
= −7 + 15
= 8
Q7. Identify monomials and binomials in the following: 4xy, -a + 8, p2, xy + 4x.
Ans:
Monomials: the expressions that have only one variable. From the given set of expressions the monomials are 4xy, p2
Binomials: the expressions that have two variables. From the given set of expressions the binomials are xy + 4x, -a + 8.
Q8. Define
(a) Like Terms
(b) Unlike Terms
Ans:
(a) Terms having the same algebraic factors are called like terms.
Example: 3pq and 7pq
(b) Terms having different algebraic factors are called unlike terms.
Example: 2xy and −3x
Q9. Find the value of equation 3x2 − 4x + 8, when x = 8.
Ans: We are given the quadratic equation of x as,
3x2 − 4x + 8
Substituting x = 8,
=3(8)2 − 4(8) + 8
=3(64) − 32 + 8
=192 − 32 + 8
=168
Q10. What should be taken away from 3x2 + 2y2 − 5xy − 25 to get −x2 − y2 + 2xy + 10.
Ans: Let the term required be p.
Hence, the required number is 4x2 + 3y2 − 7xy − 35.
Q11. From the sum of 7p + 3q + 11 and 4p − 2q − 5, subtract 3p − q + 11.
Ans: By adding coefficients of similar terms of the first two expressions we get,

By subtracting coefficients of similar terms of the above expression and third expression we get,

Q12. From the sum of 8a − 5b + 3 and 6a + 3b + 5, subtract the difference of 2a − 3b + 8 and a + 2b + 6.
Ans: By adding coefficients of similar terms of the first two expressions we get
By subtracting coefficients of similar terms of the above expression and third expression we get,
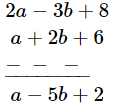
By subtracting,

Q13. Find the value of
(a) 3p2 + 4q2 − 5, when p = 3 and q = −2
(b) x3 − 3x2y + 2xy2 + 8xy + 9, when x = −3 and y = 1
Ans:
(a) 3p2 + 4q2 − 5
Substituting p = 3,q = −2,
= 3(3)2 + 4(−2)2 − 5
= 27 + 16 − 5
= 38
(b) x3 − 3x2y + 2xy2 + 8xy + 9
Ans: Substituting x = −3,y = 1,
= (−3)3 − 3(−3)2(1) + 2(−3)(1)2 + 8(−3)(1) + 9
= −27 − 27 − 6 − 34 + 9
= −54 − 30 + 9
= − 75
Q14. What should be the value of ‘p’, 3m2 + m + p = 12 when m = 0.
Ans: We are given the quadratic equation of m as,
3m2 + m+ p = 12
Substituting m=0,
3(0)2 + (0) + p = 12
p = 12
|
77 videos|386 docs|39 tests
|
















