Class 7 Maths Chapter 10 Question Answers - Exponents and Powers
Q1. Express 16807 in exponential form.
Ans: Given: 16807
We need to express the given number in exponential form.
Exponential form is a way to represent a number in repeated multiplications of the same number.
So, we can write 16807 as
16807 = 7 × 7 × 7 × 7 × 7
16807 = 75
Q2. Identify which is greater 27 or 72.
Ans: Given: exponents 27,72
We need to find which exponent is greater.
We will find the value of each exponent and then compare it.
We can write the exponents as
27 = 2 × 2 × 2 × 2 × 2 × 2 × 2
27 = 128
72 = 7 × 7
72 = 49
Clearly, we can see that
27>72
Q3. Simplify 73 × 25.
Ans: Given: 73 × 25
We need to simplify the given exponential expression.
We can simplify the given expression as
73 × 25 = 7 × 7 × 7 × 2 × 2 × 2 × 2 × 2
73 = 343 × 32
73 = 10976
Q4. Write 1024 as a power of 2.
Ans: Given: 1024
We need to write the given expression as power of 2
Break 1024 in factors of 2 and write as exponents.
Therefore, 1024 as power of 2 will be written as
1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
⇒1024 = 210
Q5. Using laws, find the value of (315 ÷ 310) × 32.
Ans: Given: (315 ÷ 310) × 32
We need to find the value of a given expression using laws.
We know that
am / an = am − n
am × an = am + n
Using these laws, the value of (315 ÷ 310) × 32 will be
= (315 ÷ 310) × 32
= 315 / 310 × 32
= 315 − 10 × 32
= 35 × 32
= 35 + 2
= 37
= 2187
Q6. Find 8 × 105 + 0 × 104 + 3 × 103 + 2 × 102 + 0 × 101 + 5 × 100.
Ans: Given: 8 × 105 + 0 × 104 + 3 × 103 + 2 × 102 + 0 × 101 + 5 × 100
We need to find the value of the given expression.
We will solve the given exponents and then add them.
Therefore, the value of 8 × 105 + 0 × 104 + 3 × 103 + 2 × 102 + 0 × 101 + 5 × 100 will be
= 8 × 100000 + 0000 + 3 × 1000 + 2 × 100 + 00 + 5 × 1
= 800000 + 0 + 3000 + 200 + 0 + 5
= 803205
Q7. Say True or False and Justify.
(a) 52 > 43
Ans: Given: 52 > 43
We need to find if the given expression is true or false.
We will solve the exponents and then compare them.
52 = 25
43 = 64
25 < 64
⇒ 52 < 43
Therefore, the expression is False.
(b) 50 = 3430
Ans: Given: 50 = 3430
We need to find if the given expression is true or false.
We will solve the exponents and then compare them.
50 = 1
3430 = 1
∴ 50 = 3430
Therefore, the expression is true.
Q8. Find the value of (30 + 20) × 51.
Ans: Given: (30 + 20) × 51
We need to find the value of a given expression.
We know that a0 = 1
Therefore, the value of (30 + 20) × 51 will be
= (30 + 20) × 51
= (1 + 1) × 5
= 2 × 5
= 10
Q9. Find (a6 / a4) × a−2 × a0 .
Ans: Given: (a6 / a4) × a−2 × a0
We need to find the value of the given expression.
We know that
am / an = am−n
am × an = am+n
a0 = 1
Therefore, (a6 / a4) × a−2 × a0 will be
=(a6−4) × a−2 × a0
= a2 × a−2 × 1
= a2+(−2)
= a0
= 1
Q10. Find 27p ÷ 272.
Ans: Given: 27p ÷ 272
We need to find the given expression.
We know that
am / an = am−n
Therefore, 27p ÷ 272 will be
=(33)p ÷ (33)2
=33p / 36
=33p−6
=33(p−2)
Q11. Express each of the following as product of prime factor
(a) 702
Ans: We need to express the given expression as product of prime factor
Exponential form is a way to represent a number in repeated multiplications of the same number.
Therefore, 702 can be written as a product of prime factors as
702 = 2 × 3 × 3 x 3 × 13
= 21 × 33 × 131
(b) 33275
Ans: Given: 33275
We need to express the given expression as a product of prime factors.
Exponential form is a way to represent a number in repeated multiplications of the same number.
Therefore, 33275 can be written as a product of prime factors as
33275 = 5 × 5 × 11 × 11 × 11
= 52 × 113
Q12. Using the laws find
(a) 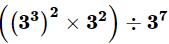
Ans: Given: 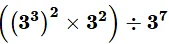
We need to find the value of a given expression using laws.
We know that
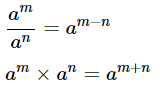
Therefore, the value of 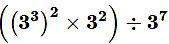 will be
will be
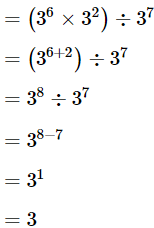
(b) 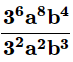
Ans: Given: 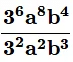
We need to find the value of a given expression using laws.
We know that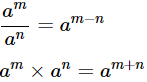
Therefore, the value of 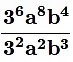 will be
will be
Q13. Express each of the following as product of prime factors
(a) 729×625
Ans: We need to express the given expression as product of prime factor
Exponential form is a way to represent a number in repeated multiplications of the same number.
Therefore, 729×625 can be written as a product of prime factors as
729 = 3 × 3 × 3 × 3 × 3 × 3
= 36
625 = 5 × 5 × 5 × 5
= 54
∴ 729 × 625 = 36 × 54
(b) 1024×216
Ans: Given: 1024 × 216
We need to express the given expression as a product of prime factors.
Exponential form is a way to represent a number in repeated multiplications of the same number.
Therefore, 1024×216 can be written as a product of prime factors as
1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 210
216 = 2 × 2 × 2 × 3 × 3 × 3 = 23 × 33
∴ 1024 × 216 = 210 × 23 × 33
= 210 + 3 × 33
= 213 × 33
Q14. Express the following as standard form
(a) 3,68,878
Ans: Given: 3,68,878
We need to express the given number as a standard form.
We will write the given numbers as a multiple of power of 10.
Therefore, the standard form of 3,68,878 will be
=3.68878 × 100000
=3.68878 × 105
(b) 4,78,25,00,000
Ans: Given: 4,78,25,00,000
We need to express the given number as a standard form.
We will write the given numbers as a multiple of power of 10.
Therefore, the standard form of 4,78,25,00,000 will be
=4.7825 × 1000000000
=4.7825 × 109
|
77 videos|386 docs|39 tests
|
FAQs on Class 7 Maths Chapter 10 Question Answers - Exponents and Powers
| 1. What are exponents and how do they work? |  |
| 2. What are the laws of exponents? |  |
| 3. How do you simplify expressions with exponents? |  |
| 4. What is the difference between a power and an exponent? |  |
| 5. Can exponents be negative or fractions? |  |
















