Introduction: Simplification & Approximation | Quantitative Aptitude for SSC CGL PDF Download
Introduction
- The Quantitative Aptitude section of the different competitive examinations consists of questions such as Simplification, Number Series, Permutation & Combination, Quadratic Equation, Data Interpretation, Data Analysis and other Miscellaneous questions.
- There are almost 10 to 12 questions in the paper which deal with topics such as Percentage and Average, ratio & proportions, partnerships, Profit & loss, calculations of simple & compound interests etc.
Here is a short study guide to help you crack questions on “Simplification and Approximation“
Basic Rules of Simplification
BODMAS Rule
- It defines the correct sequence in which operations are to be performed in a given mathematical expression to find the correct value.
- This means that to simplify an expression, the following order must be followed -
B = Bracket,
O = Order (Powers, Square Roots, etc.)
D = Division
M = Multiplication
A = Addition
S = Subtraction
- Hence, to solve simplification questions correctly, you must apply the operations of brackets first.
- Further, in solving for brackets, the order - (), {} and [] - should be strictly followed.
- Next, you should evaluate exponents (for instance powers, roots etc.)
- Next, you should perform division and multiplication, working from left to right. (division and multiplication rank equally and are done left to right).
- Finally, you should perform addition and subtraction, working from left to right. (addition and subtraction rank equally and are done left to right).
Example 1: Solve 12 + 22 ÷ 11 × (18 ÷ 3)^2 - 10
Solution:
= 12 + 22 ÷ 11 × 6^2 - 10 (Brackets first)
= 12 + 22 ÷ 11 × 36 - 10 (Exponents)
= 12 + 2 × 36 - 10 = 12 + 72 - 10 (Division and multiplication, left to right)
= 84 - 10 = 74 (Addition and Subtraction, left to right)
Example 2: Solve 4 + 10 - 3 × 6 / 3 + 4
Solution:
= 4 + 10 - 18/3 + 4 = 4 + 10 - 6 + 4 (Division and multiplication, left to right)
= 14 - 6 + 4 = 8 + 4 = 12 (Addition and Subtraction, left to right)

To Solve Modulus of a Real Number
- The Modulus (or the absolute value) of x is always either positive or zero, but never negative.
- For any real number x, the absolute value or modulus of x is denoted by |x| and is defined as
|x|= x {if x ≥ 0} and −x {if x < 0}
Exmaple: Solve |8|
Solution: |8| = |-8| = 8
Tips to Crack Approximation
Conversion of decimal numbers to nearest number
- To solve such questions, first convert the decimal to the nearest value.
- Then simplify the given equation using the new values that you have obtained.
Example1: Solve 4433.764 - 2211.993 - 1133.667 + 3377.442
Solution: Here,
4433.764 = 4434
2211.993 = 2212
1133.667 = 1134
3377.442 = 3377Now simplify, 4434 - 2212 - 1134 + 3377 = 4466
Example 2: Solve 530 x 20.3% + 225 x 16.8%
Solution: Here, 20.3% becomes 20% and 16.8% becomes 17%
Now, simplify 530 x 20% + 225 x 17%
= 106 + 38.25 = 144.25
Approximation of Square Roots
- To simplify a square root, you can follow these steps:
- Factor the number inside the square root sign.
- If a factor appears twice, cross out both and write the factor one time to the left of the square root sign. If the factor appears three times, cross out two of the factors and write the factor outside the sign, and leave the third factor inside the sign. Note: If a factor appears 4, 6, 8, etc. times, this counts as 2, 3, and 4 pairs, respectively.
- Multiply the numbers outside the sign.
- Multiply the numbers left inside the sign.
- To simplify the square root of a fraction, simplify the numerator and simplify the denominator.
NOTE: Check that the outside number squared times the inside number should equal the original number inside the square root.
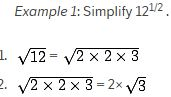


Following are some solved examples to help you prepare well for the upcoming exams:
Ques1. A man has Rs. 480 in the denominations of one-rupee notes, five-rupee notes, and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has?
A. 45
B. 60
C. 75
D. 90
 View Answer
View Answer 
Answer: Option D
Explanation:
Let the number of notes of each denomination be x.
Then x + 5x + 10x = 480
=> 16x = 480
Therefore, x = 30.
Hence, total number of notes = 3x = 90.
Ques2. There are two examinations rooms A and B. If 10 students are sent from A to B, then the number of students in each room is the same. If 20 candidates are sent from B to A, then the number of students in A is double the number of students in B. The number of students in room A is:
A. 20
B. 80
C. 100
D. 200
 View Answer
View Answer 
Answer: Option C
Explanation:
Let the number of students in rooms A and B be x and y respectively.
Then, x - 10 = y + 10 x - y = 20 .... (i)
and x + 20 = 2(y - 20) x - 2y = -60 .... (ii)
Solving (i) and (ii) we get: x = 100 , y = 80.
Therefore, The required answer A = 100.
Ques3. The price of 10 chairs is equal to that of 4 tables. The price of 15 chairs and 2 tables together is Rs. 4000. The total price of 12 chairs and 3 tables is:
A. Rs. 3500
B. Rs. 3750
C. Rs. 3840
D. Rs. 3900
 View Answer
View Answer 
Answer: Option D
Explanation:
Let the cost of a chair and that of a table be Rs. x and Rs. y respectively.
Then, 10x = 4y or y = 5/2 x.
Therefore, 15x + 2y = 4000
=> 15x + 2*(5/2)x = 4000
=> 20x = 4000
Therefore, x = 200.
So, y = (5/2) * 200 = 500.
Hence, the cost of 12 chairs and 3 tables = 12x + 3y
= Rs. (2400 + 1500)
= Rs. 3900.
Ques4. If a - b = 3 and a2 + b2 = 29, find the value of ab.
A. 10
B. 12
C. 15
D. 18
 View Answer
View Answer 
Answer: Option A
Explanation:
2ab = (a2 + b2) - (a - b)2
= 29 - 9 = 20
=> ab = 10.
Ques5. The price of 2 sarees and 4 shirts is Rs. 1600. With the same money one can buy 1 saree and 6 shirts. If one wants to buy 12 shirts, how much shall he have to pay ?
A. Rs. 1200
B. Rs. 2400
C. Rs. 4800
D. Cannot be determined
E. None of these
 View Answer
View Answer 
Answer: Option B
Explanation:
Let the price of a saree and a shirt be Rs. x and Rs. y respectively.
Then, 2x + 4y = 1600 .... (i)
and x + 6y = 1600 .... (ii)
Divide equation (i) by 2, we get the below equation.
=> x + 2y = 800. --- (iii)
Now subtract (iii) from (ii)
x + 6y = 1600 (-)
x + 2y = 800
----------------
4y = 800
----------------
Therefore, y = 200.
Now apply value of y in (iii)
=> x + 2 x 200 = 800
=> x + 400 = 800
Therefore x = 400
Solving (i) and (ii) we get x = 400, y = 200.
Therefore, Cost of 12 shirts = Rs. (12 x 200) = Rs. 2400.
Example 6: 64 × 99
 View Answer
View Answer 
Solution 6:
⇒Step 1: 64 – 1 = 63
⇒Step 2: Complement of 64 = 100 – 64 = 36
Ans: 6336.
Example 7: 678 × 999 = ?
 View Answer
View Answer 
Solution 7:
⇒Step 1: 678 – 1 = 677
⇒Step 2: Compliment of 678 = 1000 – 678 = 322
Ans: 677322.
Example 8: 78 × 999 = ?
 View Answer
View Answer 
Solution 8: Take 78 as 078 and solve normally.
⇒Step 1: 078 – 1 = 077
⇒Step 2: Compliment of 078 = 1000 – 078 = 922
Ans: 77922
Example 9: Square of number 988?
 View Answer
View Answer 
Solution 9: Nearest best to 988 = 1000. 988 is less than 100 by 12
⇒Step 1: Subtract 988 by 12 = 988 – 12 = 976.
⇒Step 2: Square of 12 = 144 (Number of digits should be equal to number of zeros in base)
Ans: 976144
Example 10: Square of number 102?
 View Answer
View Answer 
Solution: Nearest best to 102 = 100. 102 is more than 100 by 2
⇒Step 1: Add 102 by 2 = 102 + 2 = 104.
⇒Step 2: Square of 2 = 04 (Number of digits should be equal to number of zeros in base)
Ans: 10404.
|
342 videos|323 docs|185 tests
|
FAQs on Introduction: Simplification & Approximation - Quantitative Aptitude for SSC CGL
| 1. What are the basic rules of simplification? |  |
| 2. How can one effectively crack approximation questions in exams? |  |
| 3. What is the difference between simplification and approximation? |  |
| 4. What are some tips for mastering simplification and approximation for exams? |  |
| 5. How important are simplification and approximation skills in competitive exams? |  |

















