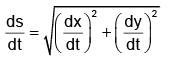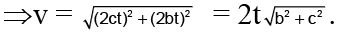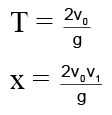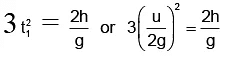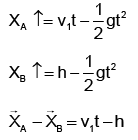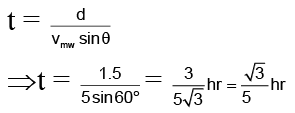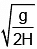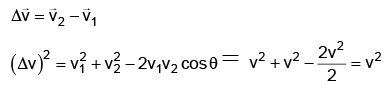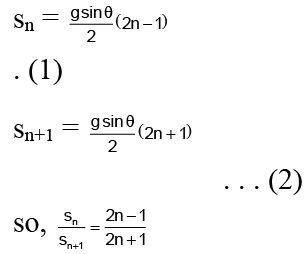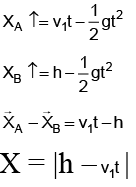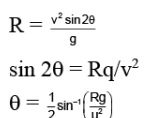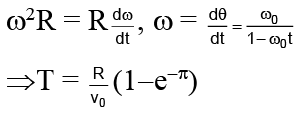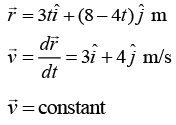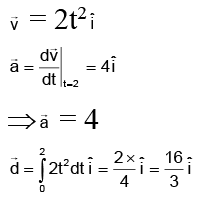Single Correct MCQs: Motion | Question Bank for JEE Main & Advanced (350+ Tests) PDF Download
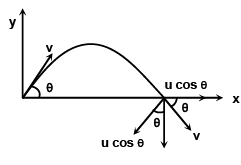
Q.1. A particle is projected upward with an initial speed u making an angle θ with the horizontal. The radius of curvature of the curve at the instant when the particle strikes the ground is
(a) 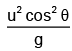
(b) 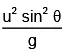
(c) u2/gsinθ
(d) u2/gcosθ
Correct Answer is option (d)
Radius of curvature R = v2/an = v2gcosθ
Q.2. The co-ordinates of a moving particle at any time t are given by x = ct2 and y = bt2. The speed of the particle is given by
(a) 2t (c + b)
(b) 2t 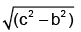
(c) t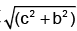
(d) 2t 
Correct Answer is option (d)
X = ct2 and y = bt2
⇒ dx/dt = 2ct & dy/dt = 2bt
Since v =
Q.3. A bus is moving with a constant velocity v1 along a horizontal road. A man standing inside the bus throws a ball upward with velocity v0 and catches the ball. The magnitude of displacement of the ball with respect to ground is
(a) 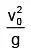
(B) zero
(c) 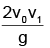
(d) 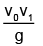
Correct Answer is option (c)
Q.4. A particle is projected vertically upwards and it attains maximum height H. If the ratio of times to attain height h (<H) is 1/3, then h equals
(a) (2/3) H
(b) (3/4) H
(c) (4/3) H
(d) (3/2) H
Correct Answer is option (b)
Let the particle be projected vertically upward with velocity u. Further, let t be the time when projectile be at height h. Then
h = ut- 1/2 gt2 or 1/2 gt2 – ut + h = 0
. . . (1)
From equation (1),
Sum of roots, t1 + t2 = - b/a = 2u/g . .. (2)Product of roots, t1t2 = c/a = 2h/g = . .. (3)
Given that t1/t2 or t2 = 3t1 .. . (4)
From equations (2) and (4), we get
4t1 = 2u/g or t1 = u/2g = . . . (5)
From equations (3) and (4), we get
or u2/2g = 4h/3 = . .. . (6)Also, maximum height, H = u2/2g . . . (7)
From Eqs. (6) and (7), we obtain
H = 4h/3 ⇒ h = 3H/4
Q.5. A body A is thrown vertically upward with initial velocity v1. Another body B is dropped from a height h at time t = 0. Which equation represents correct relationship between distance of separation between the two particles (x) and time t (before they collide with ground)?
(a) X = |h - v1t |
(b) X = |h + v1t |
(c) X = 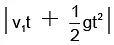
(d) X = |1/2 g2 - v1t|
Correct Answer is option (a)
X = |h - v1t |
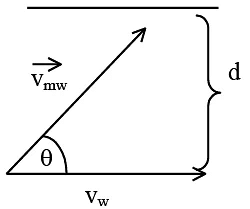
Q.6. A man can swim at a speed of 5 km/h w.r.t. water. He wants to cross a 1.5 km wide river flowing at 3 km/h. He keeps himself always at an angle of 60o with the flow direction while swimming. The time taken by him to cross the river will be
(a) 0.25 hr
(b) 0.35 hr
(c) 0.45 hr
(d) 0.55 hr
Correct Answer is option (b)
The angle betweenand
is θ (say).
⇒ The required time for crossing,
Q.7. A disc of radius R is rotating inside a room. A boy standing near the rim of the disc, finds that water droplets falling from the ceiling always hit on his head. As one drop hits his head, the next one starts from the ceiling. If height of the roof above his head is H, angular velocity of the disc is
(a) 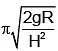
(b) 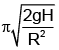
(c) 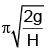
(d) 
Correct Answer is option (c)
The time period of revolution of the disc is equal to the time of motion of water drop in air.
⇒ 2πR /ω =or ω = 2πR
Q.8. A body is moving in a circle at a uniform speed v. The magnitude of the change in velocity when the radius vector describes an angle of 60° is
(a) v
(b) v/2
(c) √3/2 v
(d) v
Correct Answer is option (d)
⇒ Δv = v
Q.9. A projectile is thrown with a velocity u0 at an angle θ with the horizontal. The ratio of the rate of change of speed w.r.t. time at the highest point to that at the point of projection is
(a) g sin θ
(b) -g sin θ
(c) zero
(d) g
Correct Answer is option (c)
dv/dt (at the top) = 0
As tangential acceleration at the top = 0
dv/dt (at the starting point) = -g sin θ
So, required ratio = zero.
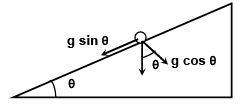
Q.10. A particle starts sliding down a frictionless inclined plane. If Sn is the distance travelled by it from time t = (n - 1) sec to t = n sec, then the ratio Sn/Sn+1 is
(a) 2n - 1/2n + 1
(b) 2n + 1/2n
(c) 2n/2n + 1
(d) 2n + 1/2n - 1
Correct Answer is option (a)
sn = u + (a/2)(2n - 1)
Q.11. A particle starts moving from rest along a circle of radius 4 m with a constant tangential acceleration of 3 m/sec2. The total acceleration of the particle at t = 2 seconds makes an angle q with the tangential acceleration, where θ is equal to
(a) tan-1(1/3)
(b) tan-1(3)
(c)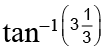
(d) 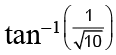
Correct Answer is option (b)
At t = 2 seconds,
v = 6 m/sec and a = 3 m/sec2 2v2/r = 36/4 = 9m/sec2
α = tan-1(3)
Q.12. A particle starts moving with constant acceleration and covers a distance x in first t seconds. The distance travelled by it in the next 2t seconds is
(a) 8x
(b) 3x
(c) x
(d) none of these
Correct Answer is option (a)
Q.13. A particle moves in the x-y plane with a velocity vx = 8t - 2 and vy = 2. If it passes through the point x = 14 and y = 4 at t = 2 s, the equation of the path is
(a) x = y2- y + 2
(b) x = y + 2
(c) x = y2 + 2
(d) x = y2 + y + 2
Correct Answer is option (a)
dx/dt = 8t - 2 ⇒ ∫ dx = ∫(8t - 2) dt
⇒ x = 4t2- 2t + c
At t = 2, x = 14 ⇒ C = 2
x = 4t2- 2t + 2 …(1)
dy/dt = 2 ⇒ ∫ dy = ∫ 2dt⇒ y = 2t + c'
At t = 2, y = 4 ⇒ c' = 0
⇒ y = 2t …(2)
From (1) and (2), eliminating t
x = y2- y + 2
Q.14. A rocket is fired upwards and its fuel is exhausted in 10 sec. The figure shows its v–t graph, where v is in m/s and t is in sec. What is the maximum height reached?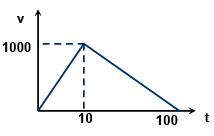
(a) 1000 x 5 m
(b) 1000 x 10 m
(c) 1000 x 50 m
(d) 1000 x 100 m
Correct Answer is option (c)
Maximum height reached = area of v–t graph = 1/2 x 100 x 1000 m.
Q.15. If the range of a gun which fires a shell with muzzle speed v is R, then the angle of elevation of the gun is
(a) 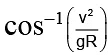
(b) 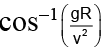
(c) 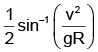
(d) 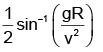
Correct Answer is option (d)
Q.16. A man starts running with constant speed along a circular path of radius 2 m. He completes two rounds in 16 seconds. The magnitude of the average velocity in first 2 seconds is
 (a) 2 m/s
(a) 2 m/s
(b) 1 m/s
(c) 3 m/s
(d) 6 m/s
Correct Answer is option (b)
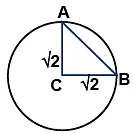
Q.17. A particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v0 at t = 0, the time for the completion of half of first revolution will be
(a) R/v0
(b)
(c) 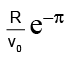
(d)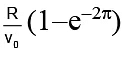
Correct Answer is option (b)
Q.18. A boy throws a ball in a train, moving at a speed of 18 kmph, with a velocity of 15√2 m/s at an angle of 45° to the horizontal in the direction of motion of the train. The angle with which it strikes the plane of projection w.r.t. an observer watching from the road nearby to the train is
(a) 45°
(b) 60°
(c) 37°
(d) none of these
Correct Answer is option (c)
Time of flight t = 2usin θ/g = 3 sec
Final velocities w.r.t. ground are
vy = u sin θ - gt = 15√2 sin 45° - 10(3) = -15m / svx = u cos θ + utrain = 15√2 cos 45° + 18 x 5/18 = 20 m / s
⇒⇒ θ = 37°
Q.19. If position vector of a particle at time t is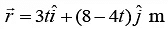 , then
, then
(a) Particle is moving with constant velocity in straight line
(b) Particle is moving with variable velocity in straight line
(c) Particle moving is in parabolic path
(d) Particle is in rest
Correct Answer is option (a)
Q.20. The velocity vector of a particle moving over a horizontal plane is given by 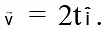 The ratio of the magnitude of instantaneous acceleration of the particle at t = 2 sec to the magnitude of displacement of the particle during the interval of first 2 sec is
The ratio of the magnitude of instantaneous acceleration of the particle at t = 2 sec to the magnitude of displacement of the particle during the interval of first 2 sec is
(a) 3/4
(b) 4/3
(c) 5/4
(d) cannot be determined
Correct Answer is option (a)