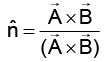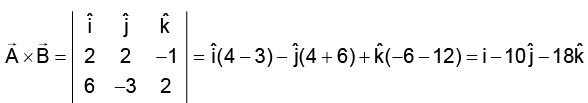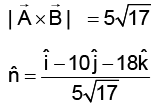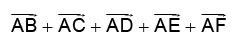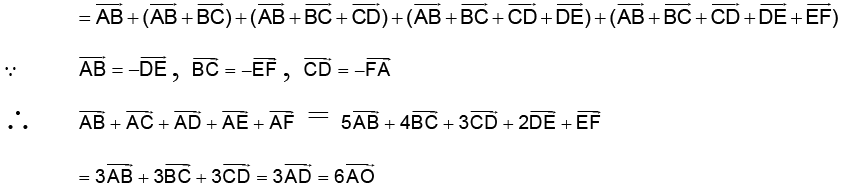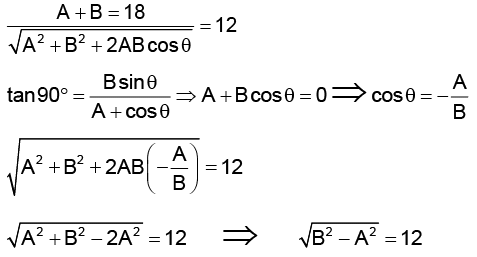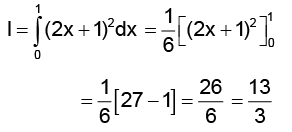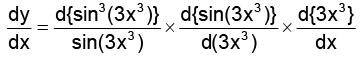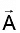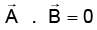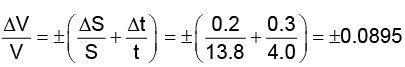Single Correct MCQs: Units & Measurement | Question Bank for JEE Main & Advanced (350+ Tests) PDF Download
Q.1. What is the unit vector perpendicular to the following vectors 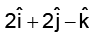 and
and 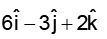 .
.
(a)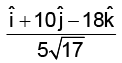
(b) 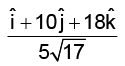
(c) 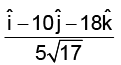
(d) 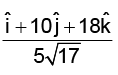
Correct Answer is option (c)
Q.2. Figure shows ABCDEF as a regular hexagon. What is the value of 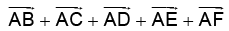 .
.
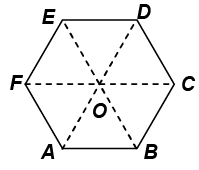
(a) 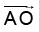
(b) 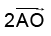
(c) 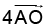
(d) 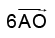
Correct Answer is option (d)
Q.3. The sum of the magnitudes of two forces acting at point is 18 and the magnitude of their resultant is 12. If the resultant is at 90° with the force of smaller magnitude, what are the, magnitudes of forces.
(a) 12, 5
(b) 14, 4
(c) 5, 13
(d) 10, 8
Correct Answer is option (c)
Let magnitude of forceis smaller than magnitude of force
We get, A = 5, B = 13
Q.4. Value of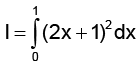 is
is
(a) 26
(b) 13
(c) 13/2
(d) 13/3
Correct Answer is option (d)
Q.5. If y = sin3(3x3), dy/dx will be
(a) cos3 (3 x)3
(b) sin3 (9x2)
(c) 27x2 sin2 (3x3) cos(3x3)
(d) 3 sin2 (3x3) cos(3x3)
Correct Answer is option (c)
y = sin3(3x3)
= 3 sin2 (3x3) x cos3x3 x 9 x2
= 27 x2 sin2 (3x3) cos(3x3)
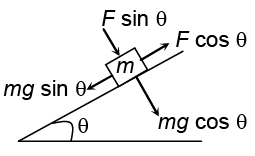
Q.6. The forces acting on a block placed on a smooth inclined plane of angle q is as shown. Net force acting on the block down the incline is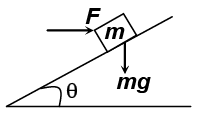
(a) m g sin θ + F cos θ
(b) m g sin θ- F cos θ
(c) m g cos θ - F sin θ
(d) m g cos θ + F sin θ
Correct Answer is option (b)
Net force down the incline
= m g sin θ - F cos θ
Q.7. Position time curve of a particle moving along x-axis is as shown in x-t curve. The position of particle at t = 4s will be,
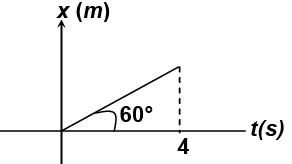
(a) 4√3m
(b) 2√3m
(c) 2 m
(d) 1 m
Correct Answer is option (a)
tan 60° = x/t
x = 4 x √3 m
Q.8. Let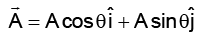 be any vector another vector
be any vector another vector 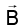 which is perpendicular to Ar can be expressed as
which is perpendicular to Ar can be expressed as
(a)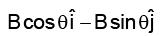
(b) 
(c) 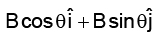
(d) 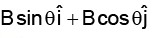
Correct Answer is option (a)
Letis perpendicular to
∴
⇒ AxBx + AyBy + AzBz = 0
Q.9. Of the following quantities, which one has dimensions different from the remaining three
(a) energy per unit volume
(b) force per unit area
(c) product of voltage and charge per unit volume
(d) angular momentum per unit mass
Correct Answer is option (d)
[energy per unit volume] = ML2T-2/L3 = ML-1T-2
[force per unit area] = MLT-2/L2 = ML-1T-2
[product of voltage and charge per unit volume] = ML–1T–2
[angular momentum per unit mass]= ML2 T–1 L. M–1 = L2T–1
Q.10. When 2.0347 is added to 15.7, the sum is
(a) 17.7347
(b) 17.734
(c) 17.73
(d) 17.7
Correct Answer is option (d)
Since, the least number of places after decimal is 1, the final result will have same. On rounding off 17.7347 to one place after decimal it becomes 17.7
Q.11. A body travels uniformly a distance of (13.8 ± 0.2) m in a time (4.0 ± 0.3) s. The velocity of the body within error limits is
(a) (3.45 ± 0.2) ms-1
(b) (3.45 ± 0.3 ) ms-1
(c) (3.45 ± 0.4 ) ms-1
(d) (3.45 ± 0.5 ) ms-1
Correct Answer is option (b)
Here S = (13.8 ± 0.2) cm ; t = ( 4.0 ± 0.3) s
∴ v = 13.8 /4.0 = 3.45ms-1
Also,
ΔV = ±0.3 (rounding off to one place of decimal)V = 3.45 ± 0.3 ms-1
Q.12. The length and breadth of a metal sheet are 3.124 m and 3.002 m respectively. The area of this sheet up to four correct significant figures is
(a) 9.376 m2
(b) 9.378 m2
(c) 9.379 m2
(d) 9.388 m2
Correct Answer is option (b)
Given length (l) = 3.124 m and breadth (b) = 3.002 m.
We know that area of the sheet
(A) = l x b = 3.124 x 3.002 = 9.378248 m2.
Since both length and breadth have four significant figures, therefore area of the sheet after rounding off to four significant figures is 9.378 m2.
Q.13. The value of universal gravitation constant G = 6.67 x 10-11 N m2 kg-2. The value of G in units of g-1 cm3 s-2 is
(a) 6.67 x 10-8
(b) 6.67 x 10-7
(c) 6.67 x 10-9
(d) 6.67 x 10-10
Correct Answer is option (a)
G = 6.67 x 10-11 Nm2 kg-2
= 6.67 x 10-11 x (kg ms-2) x (m2) x (kg)-2
= 6.67 x 10-11 x [ (1000 g ) x (100 cm) x s-2] x (100 cm)2 x (1000 g)-2
= 6.67 x 10-11 x 105 x 104 x 10-6 g-1 cm3 s-2
= 6.67 x 10-8 g-1 cm3 s-2
Q.14. If energy (E), momentum (P) and force (F) are chosen as fundamental units. The dimensions of mass in new system is
(a) E -1 P3
(b) E -1 P2
(c) E-2 P2
(d) none of these
Correct Answer is option (a)
The dimensions of E, P and F in terms of M, L and T are
[E] = ML2T-2
[P] = MLT-1
[F] = MLT-2
Let [M]= EaPb FC
or [M] = (ML2T-2)a (MLT-1)b (MLT-2)C
Equating the powers of M, L and T, we have a = -1, b = 2 and c = 0
Hence [M] = E-1 P2
Q.15. Number of particles is given by 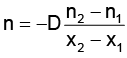 crossing a unit area perpendicular to X-axis in unit time, where n1 and n2 are number of particles per unit volume for the value of x meant to x2 and x1. Find dimensions of D called as diffusion constant
crossing a unit area perpendicular to X-axis in unit time, where n1 and n2 are number of particles per unit volume for the value of x meant to x2 and x1. Find dimensions of D called as diffusion constant
(a) M0LT2
(b) M0L2 T-4
(b) M0L T-3
(d) M0L2 T-1
Correct Answer is option (d)
[n] = Number of particles crossing a unit area in unit time = [L-2T-1]
[n2] = [n1 ] = number of particles per unit volume = [L–3]
[x2] = [x1] = positions

Q.16. If the dimensions of length are expressed as Gxcyhz ; where G, c and h are the universal gravitational constant, speed of light and Planck's constant respectively, then
(a) x = 1/2 , y = 1/2
(b) x = 1/2 , z = 1/2
(c) y = 1/2 , z = 3/2
(d) None of these
Correct Answer is option (b)
Length ∝Gxcyhz
L= [M-1L3T-2]x [LT-1]y [ML2T-1]z
By comparing the power of M, L and T in both sides we get
-x + z = 0, 3x + y + 2 z = 1 and -2x -y-z = 0
By solving above three equations we get
x = 1/2, y = -3/2, z = 1/2
Q.17. A highly rigid cubical block A of small mass M and side L is fixed rigidly onto another cubical block B of the same dimensions and of low modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of Bis rigidly held on a horizontal surface. A small force F is applied perpendicular to one of the side faces of A. After the force is withdrawn block A executes small oscillations. The time period of which is given by
(a) 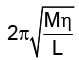
(b) 
(c) 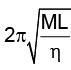
(d) 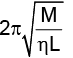
Correct Answer is option (d)
By substituting the dimensions of mass [M], length [L] and coefficient of rigidity [ML-1T-2] we get
is the right formula for time period of oscillations.
Q.18. If the constant of gravitation (G) , Planck's constant (h) and the velocity of light (c) be chosen as fundamental units. The dimension of the radius of gyration is
(a) h1/2c-3/2G1/2
(b) h1/2c3/2G1/2
(c) h1/2c-3/2G-1/2
(d) h-1/2c-3/2G1/2
Correct Answer is option (a)
Let radius of gyration [k] ∝ [h]x [c ]y [G]z
By substituting the dimension of [k ] = [L]
[h] = [ML2T-1], [c ] = [LT-1], [G] = [M-1L3 T-2]
and by comparing the power of both sides
We can get x = 1/2, y = -3/2, z = 1/2
So, dimension of radius of gyration are[h]1/2[c]-3/2[G]1/2
Q.19. In the relation 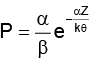 P is pressure, Z is the distance, k is Boltzmann constant and θ is the temperature. The dimensional formula of β will be
P is pressure, Z is the distance, k is Boltzmann constant and θ is the temperature. The dimensional formula of β will be
(a) [M0L2T0]
(b) [M1L2T1]
(c) [M1L0T-1]
(d) [M0L2T-1]
Correct Answer is option (a)
In given equation, αz/kθ should be dimensionless
Q.20. The dimensions of h/e (h = Planck’s constant and e = electronic charge) are same as that of:
(a) magnetic flux
(b) electric flux
(c) electric field
(d) magnetic field
Correct Answer is option (a)
Electric potential v ≡ dφ/dt ...(1)
(Faraday’s law) and eV = hv (photo-electric effect)
or V = (h/e)v ...(2)
From Eqs. (1) and (2) we can see that magnetic flux (ϕ) and h/e have the same dimensions.
FAQs on Single Correct MCQs: Units & Measurement - Question Bank for JEE Main & Advanced (350+ Tests)
| 1. What are the fundamental units of measurement in physics? |  |
| 2. How is a derived unit different from a fundamental unit? |  |
| 3. What is the SI system of units? |  |
| 4. How are prefixes used in the SI system? |  |
| 5. Why is standardization of units important in scientific measurements? |  |