Solutions of heat, wave, and Laplace's equations | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Wave Equation |

|
| Solution of Wave Equation |

|
| Heat Equation |

|
| Solution of the Heat Equation |

|
| Laplace Equation |

|
Wave Equation
One-dimensional wave equation is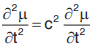 (equation of the vibration of a string).
(equation of the vibration of a string).Two-dimensional wave equation is
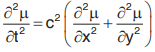 (equation of the vibration of a rectangular membrance).
(equation of the vibration of a rectangular membrance).Three-dimensional wave equation is
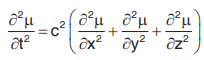
Solution of Wave Equation
Wave equation is

Let its solution be
y(x, t) = X(x) T(t) ….(2)
Substituting from Eq. (2) in Eq. (1), we get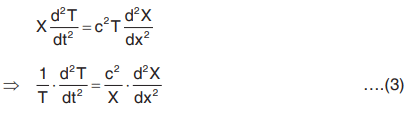
Since, x and t are independent variables and left side of Eq. (3) is a function of t alone while right side is a function of x, Eq. (3) will be true only when each side is equal to a constant :
When constant is negative (-k2)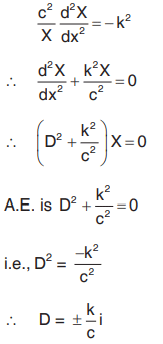
∴ Solution is X = 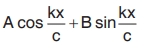
Also, 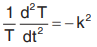

∴ Solution is T = C cos kt + D sin kt
∴ Solution for y : y(x, t) = X(x) T(t)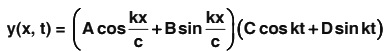
When constant is zero
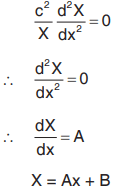
Similarly, T = (Ct + D)
Solution for y = y(x, t) = X(x) T(t) 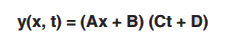
When constant is positive (k2)
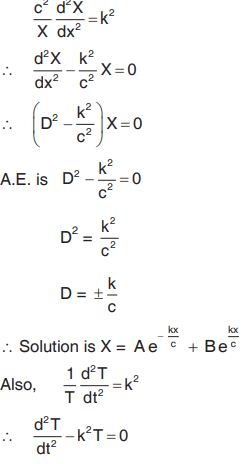
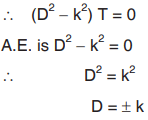
Solution is 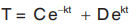
Solution for y : y(x, t) = X(x) T(t)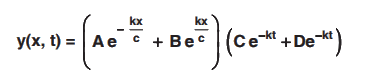
Heat Equation
One-dimensional heat equation is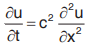 , where
, where 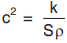 is known as diffusivity of the material of the bar.
is known as diffusivity of the material of the bar.Solution of the Heat Equation
The heat equation is 
Let u(x, t) = X(x) T(t) ….(2)
where, X is a function of x only and T is a function of t only be a solution of Eq. (1). Then, 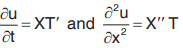
Substituting in Eq. (1),

Now, LHS of Eq. (3) is a function of x only and the RHS is a function of t only. Since, x and t are independent variable, this equation can hold only when each side is equal to a constant.
When constant is negative (-k2)
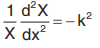
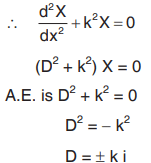
Solution is X = A cos kx + B sin kx
Also, 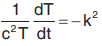
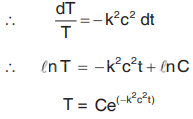
Solution for u :
u(x, t) = X(x) T(t)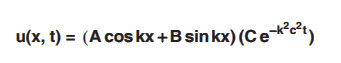
When constant is zero
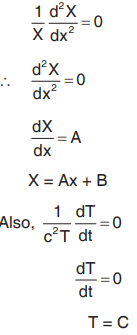
u(x, t) = (Ax + B) C
When constant is positive (k2)

Solution for u :
u(x, t) = X(x) T(t)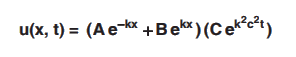
Laplace Equation
Laplace equation in two dimensions is 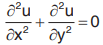
Laplace equation in three dimensions is
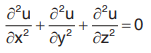
Solution of Laplace Equation in Two Dimensions
Laplace equation is

Let u(x, y) = X(x) Y(y) …(2)
where, X is a function of x only and y is a function of y only be a solution of Eq. (1).

Substituting in Eq. (1) we have X"Y + XY" = 0

Now, LHS of Eq. (3) is a function of x only and the RHS is a function of y only. Since, x and y are independent variable, this equation can hold only when each side is equal to a constant.
When constant is negative (-k2)

Solution is X = A cos kx + B sin kx
Also, 
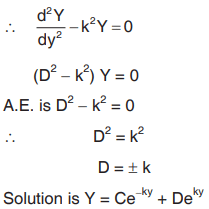
Solution for u : u(x, y) = X(x) Y(y) 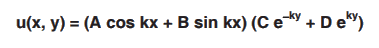
When constant is zero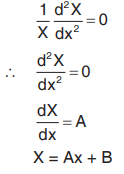
Similarly, Y = Cy + D
Solution for u : u(x, y) = X(x) Y(y)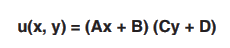
When constant is positive (k2)
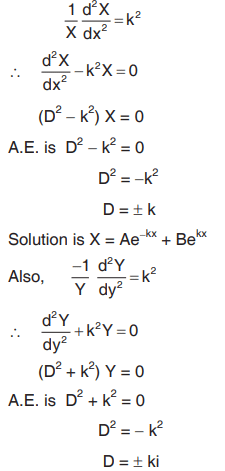
Solution for u :
u(x, y) = X(x) Y(y) 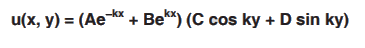
|
44 videos|109 docs|58 tests
|
FAQs on Solutions of heat, wave, and Laplace's equations - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are the key differences between the wave equation, heat equation, and Laplace's equation? |  |
| 2. How are the solutions of the heat, wave, and Laplace equations used in mechanical engineering applications? |  |
| 3. Can you provide an example of a real-world problem that can be solved using the wave equation in mechanical engineering? |  |
| 4. How does the heat equation help in determining the temperature distribution in a mechanical system? |  |
| 5. What role does Laplace's equation play in the design and analysis of mechanical systems? |  |















